地球科学进展

地球科学进展, 2021, 36(5): 528-535 DOI: 10.11867/j.issn.1001-8166.2021.018

新学科·新技术·新发现

CG6型相对重力仪比例因子两种标定结果比对分析

赵丕,, 何志堂,, 罗铖, 康胜军, 史志刚

自然资源部第一大地测量队，陕西 西安 710054

Comparison and Analysis of Two Different Calibration Results of Scale Factor of CG6 Relative Gravimeter

ZHAO Pi,, HE Zhitang,, LUO Cheng, KANG Shengjun, SHI Zhigang

The First Geodetic Surveying Brigade of Ministry of Natural Resources，Xi'an 710054，China

通讯作者: 何志堂（1972-），男，陕西西安人，高级工程师，主要从事大地测量、重力测量及相关研究工作. E-mail：547060281@qq.com

收稿日期: 2020-12-29   修回日期: 2021-03-05   网络出版日期: 2021-06-18

基金资助: 国家自然科学基金面上项目“局部地质水文特征对地表重力观测影响研究”.  41774093
国家自然科学基金青年科学基金项目“红河断裂带北、中段及邻区现今地壳深部变形的重力学研究”.  41604014

Corresponding authors: HE Zhitang (1972-), male, Xi'an City, Shaanxi Province, Senior engineer. Research areas include geodetic surveying. E-mail:547060281@qq.com

Received: 2020-12-29   Revised: 2021-03-05   Online: 2021-06-18

作者简介 About authors

赵丕（1986-），男，陕西西安人，工程师，主要从事重力测量及相关研究工作.E-mail：583954561@qq.com

ZHAOPi(1986-),male,Xi'anCity,ShaanxiProvince,Engineer.Researchareasincludegravitymeasurement.E-mail:583954561@qq.com

摘要

比例因子一直是影响相对重力测量精度的重要因素之一。根据不同方法标定相对重力仪比例因子，对相对重力测量数据进行计算，其结果精度存在一定的不同。利用CG6型相对重力仪比例因子的两种标定结果（重力长基线标定值和测区重力基准点之间标定值），对2019年和2020年中国大陆构造环境监测网络西藏测区相对重力联测数据进行处理，并对结果精度进行比对分析。结果表明，采用在测区重力基准点间标定比例因子计算的成果精度，优于在重力长基线标定比例因子计算的成果精度。

关键词： 相对重力测量 ; 比例因子 ; 重力段差 ; 精度

Abstract

Scale factor is always one of the most important factors which affect the accuracy of relative gravity measurement. The scale factors from different calibration methods are used to calculate the same relative gravity measurement data and therefore the accuracy of the results are different. Based on the different scale factors of CG6 relative gravimeter（Calibration factor calculated by the gravity long baseline or the gravity datum points in the measurement area），the gravity measurement data of Tibet area in Crustal Movement Observation Network of China in 2019 and 2020 were calculated， and then the calculated results is compared and analyzed. The results show that the accuracy calculated by calibrating the scale factor between the gravity datum points in the measurement area is better than that calculated by calibrating the scale factor on the gravity long baseline.

Keywords： Relative gravity measurement ; Scale factor ; Segment difference ; Accuracy.

PDF (2318KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

赵丕, 何志堂, 罗铖, 康胜军, 史志刚. CG6型相对重力仪比例因子两种标定结果比对分析. 地球科学进展[J], 2021, 36(5): 528-535 DOI:10.11867/j.issn.1001-8166.2021.018

ZHAO Pi, HE Zhitang, LUO Cheng, KANG Shengjun, SHI Zhigang. Comparison and Analysis of Two Different Calibration Results of Scale Factor of CG6 Relative Gravimeter. Advances in Earth Science[J], 2021, 36(5): 528-535 DOI:10.11867/j.issn.1001-8166.2021.018

1 引 言

精确的重力测量成果可以广泛地应用于地面沉降［1］、地震监测预报［2~8］、地球动力学［9］、板块地质结构［9，10］和潮汐分析［11，12］等研究以及重力基准建设［13~17］。

显然，比例因子作为相对重力仪的重要参数之一，势必对相对重力测量成果的精确性产生影响。隗寿春等［18］以2015—2016年南天山重力测网重力测量数据为基础，分别采用实测标定的格值系数与基线场的标定结果参与数据平差。结果显示，标定后的重力变化量级明显减小。得出了测网实测格值系数可以有效减弱对整体结果的影响。郝洪涛等［19］利用分测线零漂改正方法和格值系数变化检测方法，对云南2014年2期观测数据进行了处理和分析。结果显示格值系数的改正对于更清楚地反映断裂两侧的差异变化和地震的发震背景有积极作用。梁伟锋等［20］研究了不同类型重力仪一次项较稳定性及其对重力场动态变化的影响。结论显示LCR-G型及Burris型金属弹簧重力仪的一次项较稳定，基本不变，而CG5型石英弹簧重力仪的一次项逐年减小，应每年利用绝对基准进行实测标定。陈晓东等［21］给出了2种（迭代线性回归法和加权主潮波法）实用的重力仪标定方法。

目前工程上常用的比例因子标定方法［22］为基线标定：在2个已知重力基准点之间进行相对重力联测，并将两点之间的已知段差值与实测值进行比较，从而得到实测相对重力仪的比例因子。

CG6型相对重力仪是由加拿大Scintrex公司生产，采用无静电整体熔凝石英弹簧传感器，携带轻便，操作简单，但在零漂率方面与金属弹簧存在一定差距［23］。随着时间的推移，弹簧长时期漂移，测程发生改变，其比例因子会随之变化。然而相对重力仪基线比例因子标定周期一般为3~5年［18］。对于零漂率较大的CG6型仪器来说，长周期标定的比例因子会使距离标定时间较长的重力数据带入较大比例因子变化引起的误差。为了减弱此类误差对数据处理结果的影响，一般利用测区实测资料重新解算比例因子［18，20］，再进行最终处理。

为了进一步研究CG6型相对重力仪基线标定比例因子和测区实测标定比例因子对成果的影响。本文分别利用2种比例因子，对中国大陆构造环境监测网络西藏测区重力资料进行重新处理，并对结果精度进行比对分析。

2 数据来源

中国大陆构造环境监测网络（以下简称“陆态网络”）是覆盖整个中国大陆的整体重力监测网。其目标是获取中国大陆重力场动态变化信息，为中国大陆动力学研究提供重要基础信息［14，16，17］。

本次分析以2019年和2020年陆态网络西藏测区相对重力联测数据为基础。其中2019年重力点38点，测段40条；2020年重力点39点，测段41条。所有测段均采用3台CG6型相对重力仪进行往返对称观测。利用平差软件LGADJ［24］分别采用固定比例因子、实测比例因子对所测区域进行经典平差计算，对最终成果进行比对分析。

2.1　固定比例因子

本文相对重力仪固定比例因子即为仪器定期在标准重力基线上标定的比例因子。采用往返对称观测法。仪器需在已知重力测段上往返观测，获得实际观测值。利用实际观测值与已知值按公式（1）计算仪器比例因子［22］：

C=∆G12/∆g12，

式中：C为重力仪比例因子；∆G12为已知重力测段段差值，单位为10-8 m/s2；∆g12为仪器实际观测值，单位为10-8 m/s2。

2019年参与陆态网络西藏测区相对重力联测的CG6型相对重力仪有：C071、C073和C075。2020年增加仪器有：C074、C076和C077。所有相对重力仪于2018年在长基线西安（2038）—拉萨（2118）间进行比例因子的标定，得到其固定比例因子，具体结果如表1所列。

表1   CG6型相对重力仪固定比例因子表

Table 1  Fixed scale factor of CG6 relative gravimeter

序号仪器型号比例因子精度序号仪器型号比例因子精度
1C0710.999815±0.0000094C0740.999822±0.000010
2C0730.999644±0.0000125C0760.999463±0.000007
3C0750.999547±0.0000096C0771.000062±0.000001

新窗口打开| 下载CSV


2.2　实测比例因子

相对于固定比例因子，根据测区重力基准控制之间的实测结果计算的比例因子称为实测比例因子。基本思路是：以重力网中绝对重力点为基准，对2期观测数据进行平差计算，利用平差后的改后段差与绝对重力点位重力值差计算出新的实测比例因子。

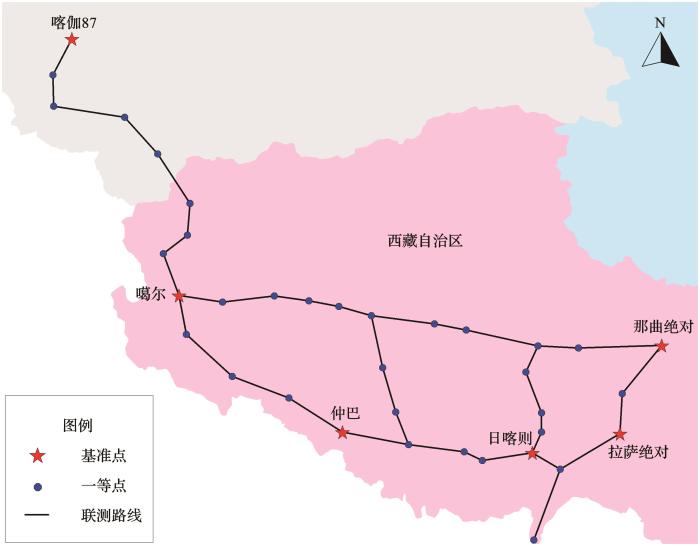
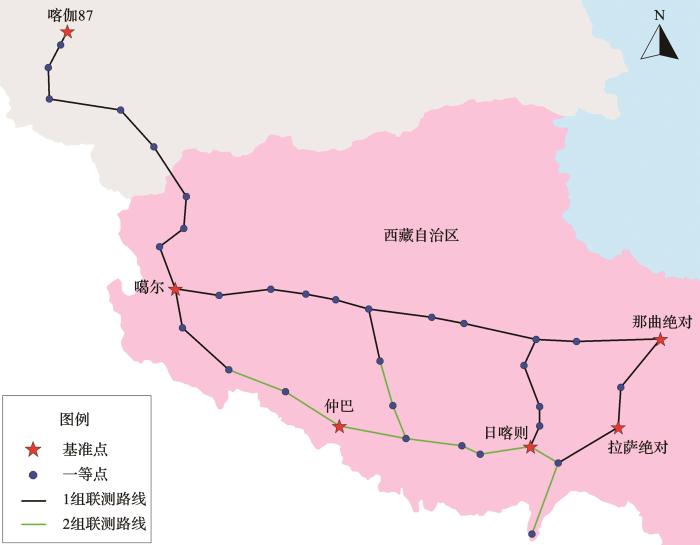
本次实测比例因子计算采用平差软件LGADJ［24，25］，分别对陆态网络西藏测区2019年和2020年相对重力联测数据进行平差计算。其采用间接平差的数学模型，平差的基本元素是重力段差的观测值，平差误差方程是以单程重力段差为观测值建立。平差计算时选取噶尔、拉萨绝对、那曲绝对、日喀则、喀伽87和仲巴6个基准点作为整体控制（具体重力网联测图如图1、2所示）。其中噶尔、拉萨绝对、那曲绝对、日喀则和仲巴5点均利用FG5绝对重力仪观测，预估精度为5×10-8 m/s2。喀伽87点利用A10绝对重力仪观测，预估精度为10×10-8 m/s2。CG6型相对重力仪预估精度为10×10-8 m/s2。每台仪器初始比例因子均设为1.000000。平差模式设置为不等精度绝对重力点经典平差。得到各台重力仪实测比例因子具体如表2所列。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   陆态网络西藏测区重力网2019年联测图

Fig.1   Gravity network in Tibet of CMONOC in 2019


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   陆态网络西藏测区重力网2020年联测图

Fig.2   Gravity network in Tibet of CMONOC in 2020


表2   实测比例因子成果表

Table 2  Measured results of scale factor

序号仪器型号2019年2020年
比例因子精度比例因子精度
1C0710.999944±0.0000110.999983±0.000016
2C0730.999806±0.0000111.000059±0.000017
3C0750.999657±0.0000110.999802±0.000019
4C074/1.000511±0.000045
5C076/1.000083±0.000045
6C077/1.000845±0.000051

注：/表示该仪器未参加2019年项目

新窗口打开| 下载CSV


从表2可知，2019年C071、C073和C075实测比例因子精度均优于2020年，2020年C071、C073和C075实测比例因子精度均优于同年度的C074、C076和C077。主要是由于2019年陆态网络西藏测区相对重力联测由1个作业小组实施，共完成40条测段，所有测段均由C071、C073和C075联测，绝对重力控制点数为6个。2020年度由2个作业小组实施，其中1组利用C071、C073和C075完成31条测段联测，绝对重力控制点数为5个；2组利用C074、C076和C077完成10条测段联测，绝对重力控制点数为2个。显然CG6型相对重力仪联测的重力网中绝对重力控制点数越多时，其相应实测比例因子精度越高。

从表1和2的比例因子成果比对可知，所有参与联测的CG6型相对重力仪比例因子均随时间推移不断增大。2018—2020年变化最小的为C071仪器，比例因子值增大0.000168，变化最大的为C077仪器，增大了0.000783。单从精度来看，固定比例因子精度略优于实测比例因子，但其相比实际变化量而言却很小。因此，对于CG6型相对重力仪而言需首先考虑比例因子随时间变化对重力成果的影响。

3 重力网平差处理

本次重力网平差与2.2小节平差主要区别在于比例因子的应用。2.2小节中各台CG6型相对重力仪均采用初始比例因子1.000000，用于计算每条测段改前段差，进一步计算各台仪器实测比例因子。本次分别将第2节中所获取的各台CG6型相对重力仪固定比例因子、实测比例因子作为实际标定结果纳入网中利用LGADJ进行整网平差。

本次整网平差，所有CG6型相对重力仪比例因子（仪器格值一次项系数）均按照实际获取的设置（按照表1、2设置）。平差控制点位及预估精度、仪器预估精度均按照2.2小节中设置。通过计算得到2019年和2020年2种不同精度平差成果，具体统计如表3所列。

表3   平差后点位精度统计表

Table 3  Statistics of point accuracy after adjustment

序号点号点名2019年精度/（×10-5 m/s2）2020年精度/（×10-5 m/s2）
固定实测固定实测
点值平均精度0.00670.00490.01310.0062
165008700喀伽870.00960.00660.01820.0072
265008701喀伽87-1//0.01970.0078
310508300阿克美其特0.00970.00670.02070.0081
410524600麻扎0.00960.00670.02030.0080
510631200康西瓦0.00950.00660.01960.0077
610237700甜水海0.00910.00630.01880.0074
710128700日土0.00710.00490.01310.0052
810127900噶尔0.00510.00350.00880.0035
910642201狮泉河重力台0.00580.00400.01060.0042
1010234100夏木0.00640.00440.01160.0045
1110234200多玛0.00800.00550.01510.0059
1210632301松西0.00870.00600.01660.0065
1310237400革吉0.00620.00430.01180.0046
1410127200巴嘎0.00640.00440.01160.0045
1510631100盐湖0.00680.00470.01330.0052
1610234000桑木桑0.00590.00410.01060.0042
1710235400达热布0.00710.00490.01400.0055
1810104400改则0.00690.00480.01380.0054
1910129700仲巴0.00480.00330.00850.0033
2010602000洞错0.00630.00440.01250.0049
2110641200措勤新0.00650.00450.01300.0051
2210632200诺仓0.00620.00430.01200.0047
2310641100拉嘎新0.00530.00370.01030.0040
2410213200拉冲0.00660.00460.01270.0050
2510127100昂仁0.00570.00400.01100.0043
2610104900尼玛0.00650.00450.01220.0048
2710601900拉孜0.00550.00380.01010.0040
2820170002申扎县0.00630.00440.01170.0046
2910128000日喀则0.00440.00300.00770.0030
3010106000亚东0.00690.00480.01380.0054
3120170374雄梅镇0.00580.00400.01080.0043
3220170003南木林0.00570.00400.01030.0041
3320170103仁堆乡0.00630.00440.01150.0045
3410233900江孜0.00500.00340.00880.0035
3510104901班戈0.00560.00390.01050.0041
3610642100拉萨绝对0.00440.00310.00780.0030
3710212800当雄0.00510.00350.00940.0037
3810130200那曲气象局0.00660.00460.01190.0047
3910130202那曲绝对0.00460.00320.00820.0032

注：/表示2019年未测该点

新窗口打开| 下载CSV


4 两种比例因子计算结果比对分析

从表3中2019年和2020年点值平均精度比对可知，采用实测比例因子的平差结果精度明显优于采用固定比例因子成果精度。为了直观理解2种比例因子对结果精度的影响，根据表3分别做2019年和2020年2种比例因子计算结果精度统计图（图3，4）。

图3

新窗口打开| 下载原图ZIP| 生成PPT

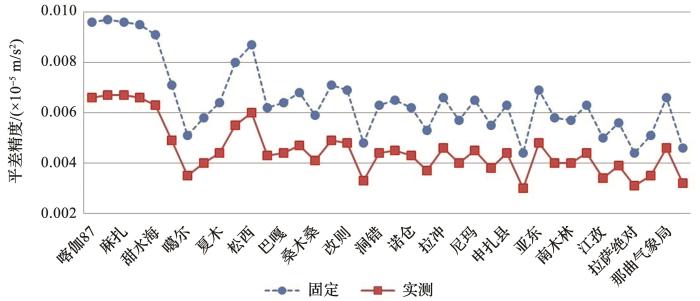
图3   2019年2种比例因子计算平差精度统计

Fig.3   Statistics of adjustment accuracy by using two kinds of scale factors in 2019


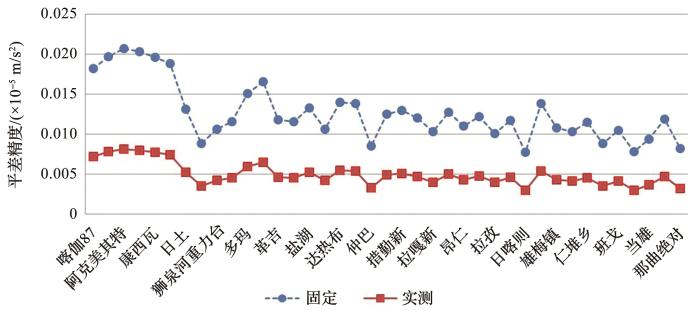
图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   2020年2种比例因子计算平差精度统计

Fig.4   Statistics of adjustment accuracy by using two kinds of scale factors in 2020


从图3和4比对结果可知，实测比例因子参与整网平差的成果精度均优于固定比例因子平差的成果精度。

5 结 论

根据陆态网2019年和2020年数据，采用固定和实测2种不同比例因子进行了计算。对2种结果进行比较得出以下结论：

（1）CG6型相对重力仪观测时间、空间跨度较大时，仪器状态会随时间、空间发生一定变化，其比例因子也会随之发生变化，因此应减短其标定有效期限。

（2）CG6型相对重力仪为石英弹簧重力仪，其联测的区域应首先利用网中绝对基准实测标定比例因子，再进行数据处理，可提高成果精度。

参考文献

CHEN Xiaodong， LI Hang， DENG Mingli，et al.

Experimental study of the surface subsidence in the city using gravity observing techniques

［J］. Chinese Journal of Geophysics，2020，63（8）： 2 882-2 892.

[本文引用: 1]

陈晓东，李航，邓明莉，等.

用重力测量技术观测城市地表下沉的实验研究

［J］.地球物理学报，2020，63（8）：2 882-2 892.

[本文引用: 1]

MAO Jinglun， ZHU Yiqing.

Progress in the application of ground gravity observation data in earthquake prediction

［J］. Advances in Earth Science， 2018， 33（3）： 236-247.

[本文引用: 1]

毛经伦，祝意青.

地面重力观测数据在地震预测中的应用研究与进展

［J］.地球科学进展，2018，33（3）：236-247.

[本文引用: 1]

ZHU Yiqing，LIANG Weifeng，ZHAO Yunfeng， et al.

Gravity changes before the Jiuzhaigou，Sichuan， MS7.0 earthquake of 2017

［J］. Chinese Journal of Geophysics， 2017，60（10）：4 124-4 131.

祝意青，梁伟锋，赵云峰，等.

2017年四川九寨沟MS7.0地震前区域重力场变化

［J］.地球物理学报，2017，60（10）：4 124-4 131.

ZHU Yiqing，LIANG Weifeng，XU Yunma.

Medium-term prediction of MS

8.0 earthquake in Wenchuan，Sichuan by mobile gravity［J］. Recent Developments in World Seismology， 2008（7）：36-39.

祝意青，梁伟锋，徐云马.

重力资料对2008年汶川MS

8.0地震的中期预测［J］.国际地震动态，2008（7）：36-39.

ZHU Yiqing，ZHANG Yong，ZHANG Guoqing，et al.

Gravity variations preceding the large earthquakes in the Qinghai-Tibet Plateau from 21st century

［J］. Chinese Science Bulletin， 2020，65（7）：622-632.

祝意青，张勇，张国庆，等.

21世纪以来青藏高原大震前重力变化

［J］.科学通报，2020，65（7）：622-632.

WANG Qinghua，ZHAO Yunfeng，CHEN Zhaohui， et al.

Gravity field change before the 2018 Mojiang M5.9 earthquake，Yunnan

［J］. Journal of Seismological Research， 2020，43（2）：382-387.

王青华，赵云峰，陈兆辉，等.

2018年云南墨江M5.9地震前的重力变化

［J］.地震研究，2020，43（2）：382-387.

DENG Mingli， SUN Heping， XU Jianqiao， et al.

Theoretical simulation of co-seismic and gravity changes of Lushan Earthquake

［J］. Earth Science， 2014，39（9）：1 373-1 382.

邓明莉，孙和平，徐建桥，等.

芦山地震同震和震后地表形变及重力变化的理论模拟

［J］.地球科学，2014，39（9）：1 373-1 382.

ZHANG Yongzhi，ZHU Guizhi， ZHU Yiqing.

Study on earthquake activities and damage evol ution by using repeated gravity observations

［J］.Crustal Deformation & Earthquake，2001（3）：14-20.

[本文引用: 1]

张永志，朱桂芝，祝意青.

利用重复重力观测资料研究地震活动与地壳的损伤演化过程

［J］.地壳形变与地震，2001（3）：14-20.

[本文引用: 1]

SUN Heping，XU Jianqiao，CUI Xiaoming.

Research progress of the gravity field application in Earth's geodynamics and interior structure

［J］.Acta Geodaetica et Cartographica Sinica， 2017，46（10）：1 290-1 299.

[本文引用: 2]

孙和平，徐建桥，崔小明.

重力场的地球动力学与内部结构应用研究进展

［J］.测绘学报，2017，46（10）：1 290-1 299.

[本文引用: 2]

WANG Jian， SHEN Chongyang， LI Hui， et al.

Gravity inversion for deep crust-mantle interface in Three Gorges region

［J］. Acta Seismologica Sinica， 2014，36（1）： 70-83.

[本文引用: 1]

汪健，申重阳，李辉，等.

三峡地区壳幔深部界面重力反演

［J］.地震学报，2014，36（1）：70-83.

[本文引用: 1]

TIAN Guie， CHEN Xiaodong， WU Shuqing， et al.

Correction of measured gravity tides with FG5 absolute gravimeter observations

［J］. Geomatics and Information Science of Wuhan University， 2020， 45（6）： 870-878.

[本文引用: 1]

田桂娥，陈晓东，吴书清，等.

FG5绝对重力仪观测数据的实测重力潮汐改正

［J］.武汉大学学报：信息科学版，2020，45（6）：870-878.

[本文引用: 1]

SUN Heping， LIU Qingchao， WU Shuqing， et al.

The latest gravity tide results in Beijing and its application in detecting resonant effect of the fluid outer core

［J］. Chinese Journal of Geophysics，2017，60（12）： 4 699-4 708.

[本文引用: 1]

孙和平，刘清超，吴书清，等.

北京地区最新重力潮汐结果及其在检测液核共振效应中的应用

［J］.地球物理学报，2017，60（12）：4 699-4 708.

[本文引用: 1]

HAN Yufei， HE Zhitang， LIU Yang，et al.

Reform and repetition measurement of Lingshan gravity calibration baseline field

［J］. Journal of Geomatics， 2017， 42（4）： 69-72.

[本文引用: 1]

韩宇飞，何志堂，刘阳，等.

灵山重力标定基线场的升级改造与复测

［J］.测绘地理信息，2017，42（4）：69-72.

[本文引用: 1]

HE Zhitang，HAN Yufei，KANG Shengjun，et al.

Initial value measurement and data analysis of Lingshan gravity baseline field in land network

［J］. Geospatial Information，2016，14（5）：100-102，108.

[本文引用: 1]

何志堂，韩宇飞，康胜军，等.

陆态网络灵山重力基线场初值测定与数据分析

［J］.地理空间信息，2016，14（5）：100-102，108.

[本文引用: 1]

Dongchen E， HE Zhitang， WANG Zemin，et al.

Establishment of absolute gravity datum in great wall station，West Antarctica

［J］. Geomatics and Information Science of Wuhan University， 2007， 32（8）： 688-691.

鄂栋臣，何志堂，王泽民，等.

中国南极长城站绝对重力基准的建立

［J］.武汉大学学报：信息科学版，2007， 32（8）：688-691.

XING Lelin，LI Hui，LI Jianguo，et al.

Establishment of absolute gravity datum in CMONOC and its application

［J］. Acta Geodaetica et Cartographica Sinica， 2016，45（5）：538-543.

[本文引用: 1]

邢乐林，李辉，李建国，等.

陆态网络绝对重力基准的建立及应用

［J］.测绘学报，2016，45（5）：538-543.

[本文引用: 1]

HE Zhitang，HAN Yufei，KANG Shengjun， et al.

Analysis of absolute gravity measurements results in the western region of phase Ⅱ China continental tectonics environmental monitoring network

［J］. Journal of Geodesy and Geodynamics， 2015，35（6）：927-930.

[本文引用: 2]

何志堂，韩宇飞，康胜军，等.“

陆态网络”Ⅱ期西部绝对重力测定结果分析

［J］.大地测量与地球动力学，2015，35（6）：927-930.

[本文引用: 2]

WEI Shouchun，ZHU Yiqing，ZHAO Yunfeng，et al.

Impact on gravity data process of scale factor coefficient of CG-5 gravimeter

［J］. Journal of Geodesy and Geodynamics，2019， 39（2）： 210-214.

[本文引用: 3]

隗寿春，祝意青，赵云峰，等.

CG-5重力仪格值系数对重力数据处理的影响

［J］.大地测量与地球动力学，2019，39（2）：210-214.

[本文引用: 3]

HAO Hongtao， LI Hui， SUN Heping， et al.

Application of zero drift correct and detection of scale parameters of CG-5 gravimeter

［J］. Geomatics and Information Science of Wuhan University， 2016， 41（9）： 1 265-1 271.

[本文引用: 1]

郝洪涛，李辉，孙和平，等.

CG-5重力仪零漂改正及格值系数检测应用研究

［J］.武汉大学学报：信息科学版，2016，41（9）：1 265-1 271.

[本文引用: 1]

LIANG Weifeng，LIU Fang，ZHU Yiqing， et al.

Research on the effect of one degree term of chromatic polynomial of gravimeter on gravity dynamic change

［J］. Journal of Geodesy and Geodynamics， 2015，35（5）：882-886.

[本文引用: 2]

梁伟锋，刘芳，祝意青，等.

重力仪一次项系数对重力场动态变化的影响研究

［J］.大地测量与地球动力学，2015，35（5）：882-886.

[本文引用: 2]

CHEN Xiaodong，SUN Heping，XU Jianqiao，et al.

Two applied methods for calibrating the gravimeters

［C］. Chinese Geophysical Society，2011：919.

[本文引用: 1]

陈晓东，孙和平，徐建桥，等.

两种实用的重力仪标定方法

［C］.中国地球物理学会，2011：919.

[本文引用: 1]

Institute of Standardization of MNR. Specifications for the gravimetry control：［S］. Beijing：Standards Press of China，2019.［自然资源部测绘标准化研究所.国家重力控制测量规范： ［S］. 北京：中国标准出版社，2019.］

[本文引用: 2]

XUAN Songbai，WANG Jian，LI Jie， et al.

Performance analysis on a new generation of the CG-6 gravimeter

［J］. Journal of Geodesy and Geodynamics， 2018，38（1）：5-7.

[本文引用: 1]

玄松柏，汪健，李杰，等.

新一代CG-6重力仪性能分析

［J］.大地测量与地球动力学，2018，38（1）：5-7.

[本文引用: 1]

LIU Shaofu，LIU Dongzhi，LI Hui.

Adjustment of high precison gravity measurement and its software

［J］. Earthquake， 1991（4）：57-58.

[本文引用: 2]

刘绍府，刘冬至，李辉.

高精度重力测量平差及其软件

［J］.地震，1991（4）：57-58.

[本文引用: 2]

XING Lelin， BAI Lei， NIU Xiaowei， et al.

A new and high-precision gravity base network in the south of the Tibetan Plateau

［J］. Geodesy and Geodynamics， 2020，11（4）：258-264.

[本文引用: 1]

/

〈 〉

地址：甘肃省兰州市天水中路8号
QQ：114723517
电话：0931-8762293　E-mail：adearth@lzb.ac.cn
陇ICP备2021001824号-5　 甘公网安备62010202000687