ADEARTH

Advances in Earth Science >

2025 , Vol. 40 >Issue 8: 864 - 876

DOI: https://doi.org/10.11867/j.issn.1001-8166.2025.063

Automated Identification of Marine Magnetic Anomaly Stripes Using U-Net Convolutional Neural Networks: A Case Study of Shatsky Rise

  • Dingzhou LIU , 1, 2 ,
  • Hongchen LIU 3 ,
  • Jinchang ZHANG , 1, 4 ,
  • Jiangyang ZHANG 1 ,
  • Pengcheng ZHOU 1 ,
  • Xin GUO 3 ,
  • Lu LI 3 ,
  • Yanming HUANG 3
Expand
  • 1. State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan 430100, China
  • 4. China-Pakistan Joint Research Center on Earth Sciences, Chinese Academy of Sciences-Pakistan Higher Education Council, Islamabad 45320, Pakistan
ZHANG Jinchang, research area includes marine geology and geophysics. E-mail:

Received date: 2025-07-05

  Revised date: 2025-08-01

  Online published: 2025-10-10

Supported by

the National Natural Science Foundation of China(42376071)

Chinese Academy of Sciences Project(Y4SL021)

Development Program of the South China Sea Institute of Oceanology, Chinese Academy of Sciences(SCSIO2024QY02)

Fold

Abstract

The discovery of marine magnetic anomaly stripes (magnetic stripes) represents a pivotal breakthrough in Earth sciences, providing decisive evidence for the theories of seafloor spreading and plate tectonics. The study of magnetic stripes is of significant scientific importance for understanding the formation and evolutionary mechanisms of oceanic lithosphere and dynamic processes within the Earth. However, traditional geological research primarily relies on manual identification of magnetic stripes, and faces several challenges: the complex structure and large volume of magnetic stripe data, the time-consuming and labor-intensive identification process, and the susceptibility of results to subjective factors such as the interpreter's experience, making it difficult to meet the efficiency and accuracy demands of modern Earth science research. To address these challenges, researchers have introduced advanced technologies, such as artificial intelligence and big data, to explore methods for the automatic identification of magnetic stripes. In this study, we targeted magnetic anomalies around the Shatsky Rise, a typical submarine feature in the western Pacific Ocean, and employed U-Net convolutional neural networks to achieve machine-automated identification of magnetic stripes. The approach first integrated marine magnetic survey data and magnetic stripe label data from the Shatsky Rise region to construct a high-quality training dataset. Subsequently, the U-Net convolutional neural network model was trained on this dataset to obtain machine-predicted magnetic stripe distributions, which were then compared and analyzed with manually identified results to validate the reliability and accuracy of the model. The study's primary findings are as follows: The study establishes a method for the automatic identification of marine magnetic anomaly stripes based on the U-Net convolutional neural network, using the Shatsky Rise as a demonstration area. It demonstrates that the U-Net-based method for automatic identification of magnetic stripes significantly improves identification efficiency and accuracy, and reduces subjective errors introduced by manual intervention. This method provides a new technical tool for the quantitative study of marine magnetic anomaly stripes. This research not only offers scientific insights for magnetic stripe identification in the Shatsky Rise region, but also provides technical support and reference models for applications in other similar areas. Thus, the findings are of significance for promoting the intelligent transformation of magnetic stripe interpretation.

Key words： Seafloor spreading; Magnetic anomaly stripes; Shatsky Rise; Artificial intelligence; U-Net.

Cite this article

Dingzhou LIU , Hongchen LIU , Jinchang ZHANG , Jiangyang ZHANG , Pengcheng ZHOU , Xin GUO , Lu LI , Yanming HUANG . Automated Identification of Marine Magnetic Anomaly Stripes Using U-Net Convolutional Neural Networks: A Case Study of Shatsky Rise[J]. Advances in Earth Science, 2025 , 40(8) : 864 -876 . DOI: 10.11867/j.issn.1001-8166.2025.063

1 海底磁异常条带背景介绍

海底磁异常条带（简称磁条带）是洋中脊扩张过程中形成的、记录地球磁场倒转历史的重要地质现象，通常呈现与洋中脊平行、正负极性交替分布的条带形态（图1）。磁条带不仅为海底扩张学说和板块运动理论提供了关键证据［3］，对研究洋壳结构、地球内部动力学过程以及板块构造演化史也具有重要的科学意义。20世纪60年代初，磁条带被首次发现［4-5］，Vine等［6］和李园洁等［7］基于海底扩张学说和地球磁场倒转理论，提出了磁条带的成因模型：在洋中脊扩张过程中，新形成的洋壳（以玄武岩为主，含部分蛇纹石化地幔物质）在冷却过程中记录下地磁极性倒转，从而形成正负磁异常相间的条带结构。20世纪60年代末，“深海钻探计划”（Deep Sea Drilling Project，DSDP）的开展进一步验证了这一模型［8］。近年来，随着超高分辨率磁测技术［如自主水下机器人（Autonomous Underwater Vehicle， AUV）近海底探测］的发展应用，已能有效揭示洋壳的精细结构［9］。同时，机器学习在磁异常自动识别与分类中的应用持续深化［10］，磁条带研究进入新阶段。新技术的发展为探索磁条带形成与演化中的关键科学问题［如洋壳磁性矿物随时间的蚀变效应对磁记录完整性的影响、板块重组过程（如俯冲起始和微板块形成）对古磁条带保存状态的制约作用等］提供了新的视角。
图1 全球海底磁条带识别数据［1-2］

黑线表示板块边界，红框为文中研究区位置。

Fig. 1 Global marine magnetic anomaly stripe identification data［1-2］

The black lines denote plate boundaries， the red box indicates the location of the study area discussed in the text.

2 磁条带识别方法发展动态

传统的磁条带识别方法主要依赖于地质学家的经验分析和人工解释，这一过程不仅耗时费力，还易受识别者经验和状态等主观因素的影响，可能导致地质解释的不一致性和不确定性。因此，学者开始引入大数据和人工智能等先进技术［11-12］，以提高磁条带识别的效率和可靠性。
近年来，研究者们开发了多种算法（如支持向量机、随机森林决策树和神经网络等）以识别磁场反转特征，部分实现了分析过程的自动化并减少了人工偏差［13-16］。然而，这些方法在一定程度上仍依赖于人工先验，且易受到历史解释的影响。此外，随着海洋磁测数据量的急剧增加，传统方法处理数据所耗费的时间显著增加。同时，数据分辨率的差异和数据伪影的存在可能进一步扭曲了对磁异常数据的解释［17］。尽管海洋磁测数据量持续增长，但其作为一种宝贵资源仍未被充分利用，加之先进分析方法的开发相对滞后，亟须发展更加客观、高效且普遍适用的分析技术，以推动相关领域的研究进展。
机器学习方法凭借其数据驱动、受主观因素影响小的优势，为海洋磁异常数据的分析提供了新的途径。近年来，基于机器学习的磁条带识别检测方法已取得了显著进展，提高了检测效率和准确性［10，18-20］。然而，现有方法主要局限于沿单个剖面的磁测数据分析，缺乏平面磁测数据分析；同时，模型训练依赖大量标注数据，而标注数据的稀缺性以及人工标注的耗时性和主观性，使得机器学习与磁条带研究的融合进展较为缓慢。虽然理论上无监督学习方法可用于磁条带预测分析，但实践经验表明，特征提取是获得合理结果的必要条件，直接将磁测数据输入模型进行预测的效果并不理想［10］。

3 沙茨基海隆地质概况

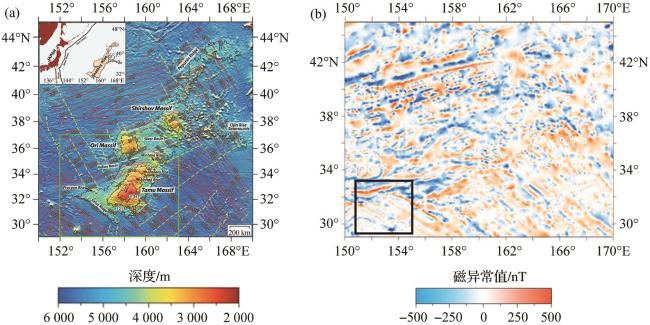
沙茨基海隆（Shatsky Rise）是坐落于西北太平洋的全球第三大洋底高原，其地理位置介于日本海沟和夏威夷岛链之间［21-22］，坐标范围为29°~45°N，150°~170°E，主体部分位于日本以东约1 500 km处［23］，总面积约53万km2（图2）。沙茨基海隆由3个主要的火山构造组成，自西向东依次为大塔穆火山（Tamu Massif）、奥里火山（Ori Massif）和希尔绍夫火山（Shirshov Massif）。其中，大塔穆火山最大、最高，顶部水深约2 000 m，基底埋深约6 500 m，总高度超过4 000 m［28］。火山具有平坦的顶峰，该特征表明火山形成过程中可能伴随广泛的海底溢流玄武岩喷发［22］。沙茨基海隆形成于晚侏罗世—早白垩世（1.45亿~1.25亿年前），与太平洋板块的早期扩张阶段同步［29-33］。沙茨基海隆的形成与中生代板块运动和地幔柱活动密切相关［34-35］，其上磁条带丰富且已经被人工识别完成，这对研究板块构造、地幔动力学、洋壳结构以及海底火山活动都具有重要的科学价值。
图2 沙茨基海隆区域［24-27］

（a）位置图：红线是磁条带，黄色虚线是断裂带，绿色框为沙茨海隆上最大的高地大塔穆火山的分布区域；（b）地磁异常图：黑色框指示图4切割的局部区域所在位置（29°4′~33°20′N，150°40′~154°56′E）。

Fig. 2 Shatsky Rise［24-27］

（a） Location map： the red lines represent magnetic stripes， the yellow dashed lines denote fracture zones， the green box marks the distribution area of the Tamu Massif， the largest edifice within Shatsky Rise； （b） Magnetic anomaly map： the black box indicates the location of Figure 4 （29°4′~33°20′N，150°40′~154°56′E）.

4 数据与方法

本文基于U-Net卷积神经网络的模型框架来实现磁条带自动识别，旨在提升磁条带识别效率、可靠性与客观性。自动识别模型的实现过程包括3个阶段：首先对沙茨基海隆区域的磁异常数据和已有的磁条带标签数据进行网格化处理；其次将网格数据分割后输入U-Net模型进行训练；最后对沙茨基海隆区域进行磁条带预测。
具体而言，本文在已有人工识别区域，通过对比模型预测结果与人工解释结果以验证模型的准确性；随后，在缺乏人工识别区域则利用模型进行预测，提供新的磁条带识别信息；最终使用全区数据训练模型并完成整体预测。

4.1　数据与预处理

本文以西北太平洋沙茨基海隆区域为研究对象（图2）。使用的海洋磁测网格化数据体源自EarthRef.org数据库（ERDA 2423数据集，http：//earthref.org/ERDA/2423/）。该数据体整合了多源观测数据［36］，包括美国国家环境信息中心（NCEI，https：//www.ngdc.noaa.gov/mgg/geodas/）和最新实施的大塔穆火山FK151005航次磁测数据。数据集历时跨度54年，涵盖96个航次共计550万个观测点，其中FK151005航次在大塔穆火山上采用高密度网格化观测方案，获取了17个横断面189万个高精度数据点。该数据体的数据处理流程具体步骤如下［24］：①通过异常值检测算法剔除受仪器噪声和地磁暴干扰的异常数据；②应用国际地磁参考场（International Geomagnetic Reference Field，IGRF）模型进行内源场校正；③基于综合模型第四代（CM4）消除外源场影响；④构建多源数据时空匹配框架，重点校正卫星导航时代前的导航误差：以GPS定位数据为基准框架，采用动态时间规整（Dynamic Time Warping，DTW）算法对历史航迹数据进行空间配准，经检验导航误差引起的交叉点误差平均值由原始数据的±5 nT降低至±1.2 nT。
本研究区域中构建了空间分辨率为1'×1'的磁异常网格数据体（961×1 201网格节点）。为适配U-Net卷积神经网络的输入要求，采用滑动窗口法进行数据分块处理：设置256×256网格的采样窗口，在经纬向分别以10个网格步长（即10'）实施滑动切割（即每次切割均向右平移10'，一行切割完毕后向下移动10'，重复相同方式继续切割）。该方案通过92.5%的窗口重叠率有效保持构造特征的连续性，同时生成9 216个训练样本，为后续模型训练提供了充分的空间特征学习基础和可靠的数据基础。
本文使用的磁条带标签数据来源于全球海底磁异常数据库（http：//www.soest.hawaii.edu/PT/GSFML/），该数据库由夏威夷大学地球物理与行星研究所维护，数据格式参考了该数据库发布的标准规范（http：//www.soest.hawaii.edu/PT/GSFML/contribute.html）。在数据处理过程中，我们基于研究需求对原始数据进行了筛选和提取，主要保留了3个关键参数：磁条带名称、地理坐标（经度和纬度）以及磁异常值。这些核心参数为后续开展磁条带可视化分析和构造解释提供了必要的基础数据支撑。

4.2　 U-Net卷积神经网络架构

U-Net是一种广泛应用于图像分割任务的卷积神经网络架构，以其独特的U型结构而得名［37］。该架构在生物医学影像分割和自然图像分割等领域取得了显著成效。本文采用传统的U-Net神经网络模型，其网络结构具有对称性，主要由编码器和解码器2部分组成。编码器由一系列卷积层和池化层构成。每个卷积层后接ReLU激活函数和归一化处理，用于提取输入图像的特征。池化层通过最大池化操作将特征图的空间维度减半，同时增加特征图的通道数，从而实现降采样。解码器则由一系列反卷积层和卷积层组成，通过上采样逐步恢复特征图的空间分辨率。上采样可通过转置卷积或双线性插值实现，每次上采样后，特征图的空间维度翻倍，最终将特征图还原至与输入图像相同的尺寸。U-Net的核心创新在于其跳跃连接机制［38］，该机制将编码器的输出与解码器的输入相连接，通过特征图拼接实现特征融合。这一设计使解码器能够充分利用编码器提取的高分辨率特征，从而更好地恢复图像的细节信息。
U-Net网络模型采用带权重的负交叉熵损失函数来评估模型预测值与真实值之间的差异。损失函数为非负实值函数，其值越小，表明模型的训练效果越好、预测准确率越高。在监督学习下，损失函数与准确率是评估模型性能的2个核心指标，二者存在以下联系：首先，其目标具有一致性，共同致力于提升模型的泛化性能；其次，当损失函数的值下降时，模型的准确率会上升，即损失函数值的优化与准确率提升之间存在正相关趋势。通过梯度下降等优化算法最小化损失函数的过程，实质上是驱动模型参数朝着预测分布与真实分布差异减小的方向更迭，通过不断调整神经网络的相关参数，使预测结果逐步逼近真实值。
本文采用U-Net网络架构通过逐像素归一化指数函数实现语义概率分布建模［37］，该函数的数学表达式定义如下：
p k x = e a k x ∑ k ' = 1 K e a k ' x
式中： a k ( x ) ∈ R为网络末端第 k个特征通道在像素位置 x处的激活值； a k ' ( x )表示在像素位置x处，所有k个类别通道的激活值集合； K ∈ N +为语义类别总数。该函数将多通道输出映射为具有概率解释的语义分布，其中 p k ( x ) ∈ [ 0,1 ]表征像素 x归属于第 k类别的后验概率。
网络优化采用加权交叉熵损失函数E，其形式化定义为：
E = ∑ x ∈ Ω ω x l o g p l x x
式中： x ∈ Ω表示像素x均位于二维离散图像空间， p l ( x )表示像素 x在其真实类别通道上的预测概率值。本文引入了一个权重项 ω ( x )以优化损失函数的计算。考虑到语义分割任务中物体边界区域对语义区分度的关键性要求，本文提出对这些区域对应的损失函数权重系数进行自适应增强，从而有效提升模型对边缘特征的提取能力。

5 模型训练与预测结果

为了充分评估U-Net模型在有限数据条件下的训练与预测性能，本文根据磁条带区域数据在训练集中的可用程度，设计了3种不同的实验方案：首先，在“完全已知”条件下，预测区域的磁条带数据全部包含在训练集中，模型能够充分利用完整的先验信息进行学习；其次，在“部分已知”条件下，预测区域的磁条带数据仅有50%参与模型训练，理论上这50%的磁条带数据可以随机选取，而此次取自每次分割图像的下半部分区域（只有log_33需预测下半部分，所以取自上半部分），用以评估模型在数据不完备情况下的泛化能力；最后，在“完全未知”条件下，预测区域的磁条带数据完全未参与模型训练，旨在测试模型对全新区域的数据外推能力。这种渐进式的实验设计能够系统性地考察模型在不同数据可用性条件下的表现差异。

5.1　磁条带完全已知的预测模型

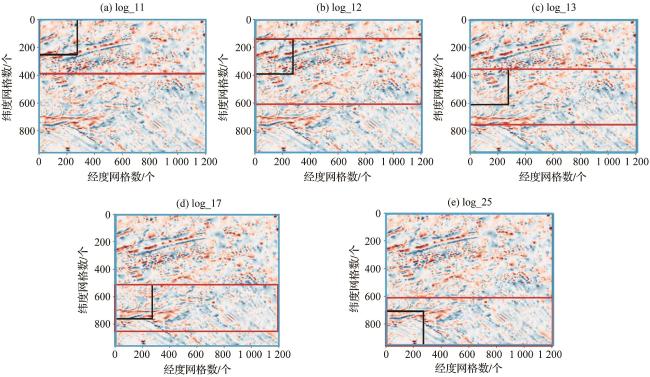
为系统评估模型在磁条带已知区域的预测性能及其泛化能力，本文采用分区训练与预测的方法，将沙茨基海隆整体区域划分为5个相互独立的小区块，分别进行模型训练与预测验证。具体划分方案如下：将整个网格区域沿纬度方向划分为5个子区域，总计70行。其中，第一个子区域选取0~14行，第二个子区域选取15~35行，第三、第四和第五个子区域分别选取；36~48行、49~60行和61~70行作为预测集，其余部分作为训练集（图3）。这种分区设计虽然并非完全均分，但也确保了每个数据点均有机会参与训练与预测过程，从而全面评估模型在不同区域的预测效果及其稳定性。通过这种分区训练与预测方法，本研究不仅能够评估模型在已知区域的预测精度，还能分析模型对局部特征的捕捉能力及其在不同区域的适应性。此外，该方法有效避免了数据泄露问题，确保了评估结果的客观性和可靠性。图4展示了沙茨基海隆局部区域的预测结果，为后续分析提供了直观的参考依据。
图3 磁条带完全已知的数据集分布图

（a）子区域一模型log_11；（b）子区域二模型log_12；（c）子区域三模型log_13；（d）子区域四模型log_17；（e）子区域五模型log_25。蓝框为训练集区域，5个模型的训练集均为沙茨基海隆整体区域，红框为预测集区域，随着子区域的变化，预测集区域在逐渐向下平移，黑框为分割窗口大小，选取不同子区域黑框所在行的模型预测结果整合成最终磁条带预测图，横纵坐标网格单位长度为经纬度的1'。

Fig. 3 Distribution map of the dataset with fully known magnetic stripes

（a） Subregion 1 model log_11； （b） Subregion 2 model log_12； （c） Subregion 3 model log_13； （d） Subregion 4 model log_17； （e） Subregion 5 model log_25. The blue boxes indicate the training set areas—the training set for all five models covers the entire Shatsky Rise region. The red boxes denote the prediction set areas， which shift gradually downward across the subregions. The black boxes represent the segmentation window size. Predictive results from models corresponding to the row in which the black box is located in each subregion are integrated to generate the final magnetic stripe prediction map. The grid units along the horizontal and vertical axes represent 1 arc-minute of latitude and longitude.

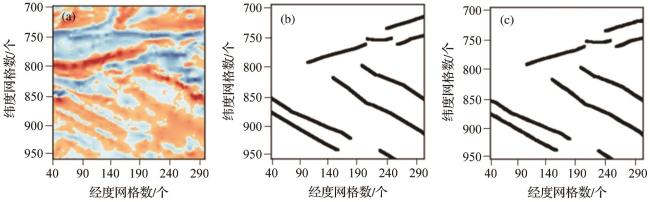
图4 沙茨基海隆局部区域

（a）地磁异常网格图；（b）人工识别磁条带标签；（c）模型log_25预测结果。图（a）具体位置为29°4′~33°20′N，150°40′~154°56′E，与图2（b）中的黑色方框所在区域相对应，横纵坐标的单位长度为经纬度的1'。

Fig. 4 Local area of Shatsky Rise

（a） Gridded magnetic anomaly map； （b） Manually identified magnetic stripe labels； （c） Prediction results from model log_25. The area shown in （a） corresponds to 29°4′~33°20′N，150°40′~154°56′E， marked by the black box in Figure 2（b）. The grid units along both axes represent 1 arc-minute in latitude and longitude.

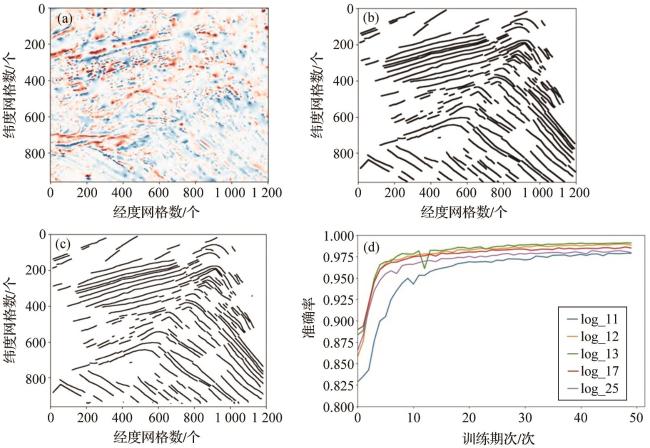
针对研究区［图5（a）］的5个子区域，分别构建了独立的U-Net模型进行训练，并依次命名为log_11、log_12、log_13、log_17和log_25（并无特殊含义，其中训练失败的模型导致命名的数字不连续）。在训练过程中，加入真实标签数据［图5（b）］，且每个模型均经过50次训练期次的迭代优化。实验结果表明，所有模型在训练过程中均呈现出良好的收敛趋势，具体表现为预测准确率逐步提升，损失函数值持续下降。通过对比分析各模型的最终性能指标，发现log_13模型展现出最优的预测性能，其预测准确率达到99.09%，同时损失函数值降至0.026 83，明显优于其他模型。这一结果不仅验证了分区训练策略的有效性，也为后续研究提供了可靠的模型选择依据。
图5 沙茨基海隆磁条带完全已知对比图

（a）地磁异常网格图；（b）人工识别磁条带标签；（c） 模型预测结果；（d）不同模型预测准确率。

Fig. 5 Comparative chart of the fully known magnetic stripes in Shatsky Rise

（a） Gridded magnetic anomaly map； （b） Manually interpreted magnetic stripe labels； （c） Model prediction results； （d） Prediction accuracy of different models.

将U-Net模型预测得到的5个子区域数据进行空间整合，生成了完整的区域预测图［图5（c）］。将预测结果与真实标签数据进行可视化对比分析，得出以下结论：在已知磁条带标签数据的监督学习下，U-Net模型展现出优异的预测性能［图5（d）］。具体而言，模型输出的预测结果与真实标签数据在空间分布和形态特征上均呈现出高度一致性，其预测准确率高。这一结果表明，在训练过程中引入已知区域的标注信息，能够显著提升模型对该区域的预测精度。从模型性能评估的角度来看，U-Net网络架构在磁条带数据预测任务中表现出良好的特征提取能力和空间信息保持能力，验证了该模型在处理此类空间预测问题上的有效性和可靠性。

5.2　磁条带部分已知的预测模型

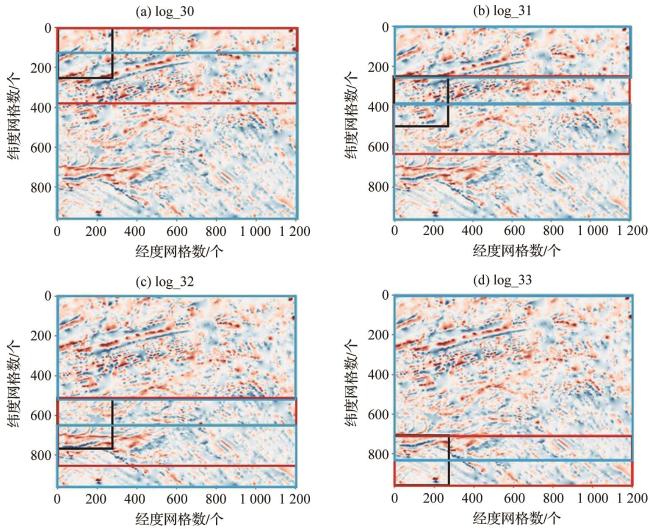
为系统评估模型在磁条带部分已知情况下的预测性能，本文设计并实施了部分已知预测实验。实验采用256×256像素（边长对应经纬度上的一分）的分割图像作为基础单元，在训练过程中仅提供50%的已知标签数据用于模型训练。具体实验设计包含4个部分：第一部分以0~12行为预测区域，12~70行为训练区域；第二部分以25~38行为预测区域，0~1行和38~70行为训练区域；第三部分以50~60行为预测区域，0~30行和66~70行为训练区域；第四部分以69~70行为预测区域，0~56行为训练区域（图6）。
图6 磁条带部分已知的数据集分布图

（a）子区域一模型log_30；（b）子区域二模型log_31；（c）子区域三模型log_32；（d）子区域四模型log_33； 蓝框为训练集区域，红框为预测集区域，黑框为分割窗口大小，选取不同子区域黑框所在行的模型预测结果整合成最终磁条带预测图，横纵坐标网格单位长度为经纬度的1'。

Fig. 6 Distribution map of the dataset with partially known magnetic stripes

（a）Subregion 1 model log_30； （b）Subregion 2 model log_31； （c） Subregion 3 model log_32； （d） Subregion 4 model log_33. The blue boxes indicate the training set areas， the red boxes represent the prediction set areas， and the black boxes denote the segmentation window size. The model prediction results from the row where the black box is located in different subregions are integrated to form the final magnetic stripe prediction map. The grid units along the horizontal and vertical axes represent 1 arc-minute of latitude and longitude.

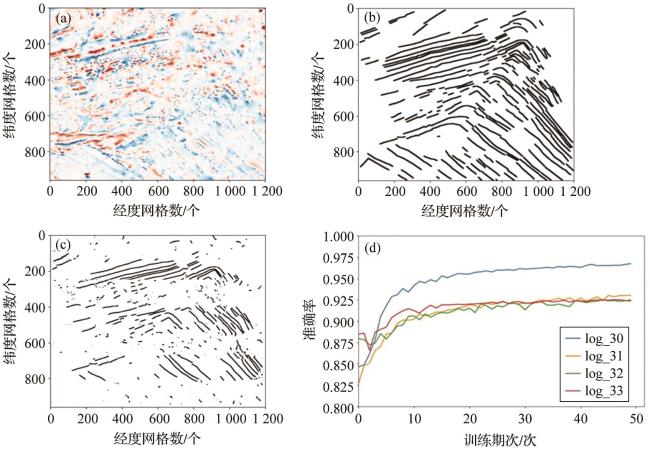
基于上述分区训练策略，本文针对整体区域［图7（a）］的4个子区域分别构建了独立的U-Net模型，依次命名为log_30、log_31、log_32和log_33，每个模型均经过50次训练期次的迭代优化。通过将4个子区域的预测结果进行空间整合，并与真实标签数据进行对比分析［图7（b）和图7（c）］后发现：在提供标签数据的训练区域，模型预测准确率较高；在未提供标签数据的区域，预测结果相对欠佳。定量分析表明，模型在磁条带部分已知情况下的预测准确率随着训练期次的增加而逐步提升［图7（d）］，但在验证集上的损失函数值也在不断升高，表明随着训练进程的推进，在部分已知情况下模型的预测性能可能发生潜在退化。总体而言，沙茨基海隆部分已知预测图呈现出明显的条带状分布特征，其中提供标签数据的3行区域预测效果较好，而其余未提供标签数据的区域预测结果较为稀疏，连续性相对较差。
图7 沙茨基海隆磁条带部分已知对比图

（a）地磁异常网格图；（b）人工识别磁条带标签；（c） 模型预测结果；（d）不同模型预测准确率。

Fig. 7 Comparative chart of the partially known magnetic stripes in Shatsky Rise

（a） Gridded magnetic anomaly map； （b） Manually interpreted magnetic stripe labels； （c） Model prediction results； （d） Prediction accuracy of different models.

值得注意的是，受分割区域大小（256×256像素）的限制，本研究无法将用于模型训练所需的50%标签数据均匀分配至图像的每行每列，这在一定程度上影响了预测结果的整体质量。这一局限性，明确了后续研究的重要改进方向，包括优化标签数据分配策略、探索更有效的半监督学习方法等，这些问题的解决将有助于进一步提升模型在磁条带半已知情况下的预测表现。

5.3　磁条带完全未知的预测模型

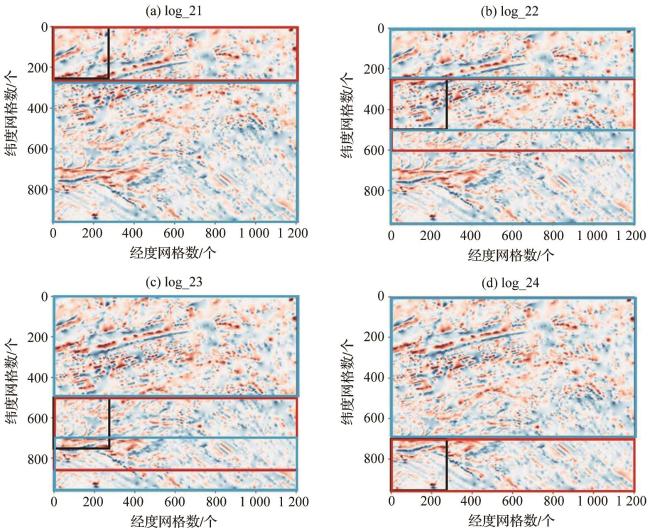
为深入验证模型对磁条带完全未知情况下的预测能力，本文设计并实施了完全未知的预测实验。实验选取4个独立区域进行训练与预测，确保预测区域完全未被标签数据覆盖。具体划分方案如下：第一部分以0~10行为预测区域，25~70行为训练区域；第二部分以25~35行为预测区域，0~1行和50~70行为训练区域；第三部分以50~60行为预测区域，0~25行和69~70行为训练区域；第四部分以69~70行为预测区域，0~45行为训练区域（图8）。
图8 磁条带完全未知的数据集分布图

（a）子区域一模型log_21；（b）子区域二模型log_22；（c）子区域三模型log_23；（d）子区域四模型log_24； 蓝框为训练集区域，红框为预测集区域，黑框为分割窗口大小，选取不同子区域黑框所在行的模型预测结果整合成最终磁条带预测图，横纵坐标网格单位长度为经纬度的1'。

Fig. 8 Distribution map of the dataset with completely unknown magnetic stripes

（a） Subregion 1 model log_21； （b） Subregion 2 model log_22； （c） Subregion 3 model log_23； （d） Subregion 4 model log_24. The blue boxes indicate the training set areas， the red boxes represent the prediction set areas， and the black boxes denote the segmentation window size. The model prediction results from the row where the black box is located in different subregions are integrated to form the final magnetic stripe prediction map. The grid units along the horizontal and vertical axes represent 1 arc-minute of latitude and longitude.

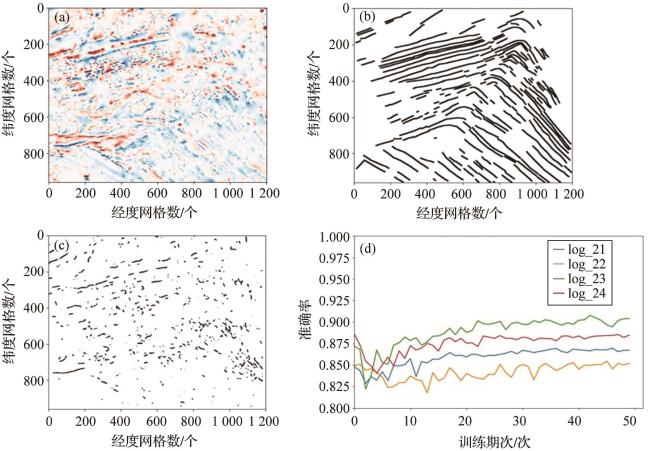
针对上述整体区域［图9（a）］的4个子区域分别构建了独立的U-Net模型，依次命名为log_21、log_22、log_23和log_24，每个模型均经过50次训练期次的迭代优化。我们将整合后的预测结果与真实标签数据［图9（b）和图9（c）］进行对比分析后发现：模型对完全未知区域的预测效果整体较差，仅能预测出磁条带的整体轮廓，且连续性较差，数据分布相对稀疏。虽然这一结果对分析海底地质成因具有一定的借鉴意义，但总体而言未能达到理想效果。
图9 沙茨基海隆磁条带完全未知对比图

（a）地磁异常网格图；（b）人工识别磁条带标签；（c）模型预测结果；（d）不同模型预测准确率。

Fig. 9 Comparative chart of the completely unknown magnetic stripes in Shatsky Rise

（a） Gridded magnetic anomaly map； （b） Manually interpreted magnetic stripe labels； （c） Model prediction results； （d） Prediction accuracy of different models.

观察预测准确率的变化趋势［图9（d）］可以发现：虽然模型对未知区域的预测准确率随着训练期次的增加而逐步提升，但与磁条带完全已知和半已知情况下的预测实验相比，针对未知区域的准确率明显偏低。与预测精度提升形成对比的是，模型在验证集上的损失函数值也在不断升高，该现象表明随着训练进程的推进，模型在磁条带未知区域的预测性能可能发生潜在退化，这与交叉验证中观察到的过拟合特征吻合。这表明在磁条带完全未知的预测任务中，模型性能仍有较大的提升空间。因此，未来工作需进一步优化模型结构，增加磁异常数据及标签数据的数量，以提升模型的预测表现。
值得注意的是，由于分割区域大小（256×256像素）的限制，log_23模型未能完全实现未知预测。然而，由于该模型对第三部分子区域的预测结果与log_24模型预测的第四部分子区域存在重叠，本文舍去了log_23模型预测的重复区域数据，保留了log_24模型预测的重复区域数据，从而确保最终整体区域的预测结果不受影响。

6 讨 论

本文提出的U-Net网络架构能够从磁异常数据中有效识别磁条带，以下将重点讨论可能影响解释结果及其未来应用潜力的关键因素。
在数据预处理阶段，本文采用纬度和经度作为磁异常的空间坐标，用于构建训练数据集并训练神经网络以实现磁条带预测。通过对比分析沙茨基海隆区域3种不同训练模型的预测结果，我们发现模型的预测性能与其训练数据集存在明显的相关性。具体而言，在磁条带已知的训练下，模型对磁条带已知区域的预测准确率可达99.08%；然而，当预测区域的磁条带标签数据未参与训练时，预测效果明显下降，这在沙茨基海隆磁条带半已知预测图中表现得尤为显著。值得注意的是，磁条带完全未知情况下，预测模型的准确率虽然只有85.11%，但该数值包含了对数据空白区域的预测结果，若仅考虑存在磁条带的区域，排除空白区的影响，实际预测准确率将更低。
其次，需要指出的是，本文在数据处理过程中未考虑经度与纬度地理距离的变化，即假设经度（和纬度）之间的间距相等，将数据视为等矩形投影。虽然这种方法可能导致解释方位角的轻微偏差，但我们的分析主要关注相对方向差异而非绝对方位角值。此外，由于我们的分割预测分析是在256×256像素的窗口中进行的，窗口面积约为22.4万km2，在该尺度下，经度间距相等的假设所引入的偏差占窗口面积的0.7%~1.6%，偏差远小于窗口面积，对整体分析的影响微乎其微，因此可以忽略不计。
另外，本文验证了U-Net网络在磁异常数据分割任务中的独特优势，其对称编码器—解码器结构通过跳跃连接实现了局部细节特征与全局语义信息的有效协同，在磁条带已知情况下小窗口分割任务展现出99.08%的预测准确率，明显优于传统阈值分割方法（如边缘检测算法）［39］。这一性能归功于U-Net对局部空间模式的高敏感性，其多尺度特征提取机制能够精准捕捉磁条带的线性延展特征与弱异常信号的空间关联性。然而，U-Net的架构特性也带来以下应用局限：首先，特征表达的区域依赖性导致模型泛化能力受限，当训练数据与预测区域存在明显地磁特征差异时，预测准确率会受到影响，表明其深层语义表征缺乏跨区域的鲁棒性（即模型在面对输入数据的变化，如噪声、分布偏移、异常值或未见过的场景时，缺乏仍能保持稳定性能的能力）；其次，等矩形投影假设下的空间偏差累积效应虽在小尺度窗口（256×256像素）中可忽略，但在大范围拼接预测时会引发方位角系统性偏移；第三，模型对标注数据规模的强依赖性凸显了其在少样本场景中的瓶颈，在磁条带完全未知的情况下，磁条带分割准确率因数据空白区域干扰而存在虚高现象，实际有效预测精度需通过区域加权评估方法进行重新标定。
该模型的未来改进可基于磁异常数据的特殊性进行架构优化：一方面，可引入动态空间注意力模块替代固定跳跃连接，通过自适应特征选择机制缓解区域特征差异导致的泛化衰减［40-41］；另一方面，结合自监督预训练策略挖掘未标注磁条带的隐含规律，可能突破现有模型对磁条带标注数据的依赖。此外，针对球面投影变形问题，开发基于球面卷积的U-Net变体或将成为提升大尺度地质构造解释精度的关键方法［42］。

7 结 论

本文提出了一种基于U-Net卷积神经网络的磁条带自动识别模型，该模型通过整合海洋磁异常数据及其对应的磁条带标签数据，实现了对磁条带的智能化分析预测。然而，基于深度学习的磁条带预测研究面临训练图像需求量大与标签数据稀缺的双重挑战。实验结果表明，当前训练完成的U-Net网络模型在磁条带已知的预测中表现出较高的准确率，但磁条带未知时的预测性能仍有待提升，这凸显了进一步扩充训练数据集的必要性。随着模型训练效果的持续优化，未来有望实现对磁条带未知区域的精确预测，从而为地质解释提供更好的技术支持。本文提出的磁条带自动识别方法具有重新审视全球海洋磁异常图的潜力，可以识别出以往未被发现的特征，为洋壳形成演化研究提供新的见解。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
SETON M， WHITTAKER J M， WESSEL P， et al. Community infrastructure and repository for marine magnetic identifications［J］. Geochemistry， Geophysics， Geosystems， 2014， 15（4）： 1 629-1 641.

[2]
SETON M， MÜLLER R D， ZAHIROVIC S， et al. A global data set of present-day oceanic crustal age and seafloor spreading parameters［J］. Geochemistry， Geophysics， Geosystems， 2020， 21（10）. DOI：10.1029/2020GC009214 .

[3]
VINE F J. Spreading of the ocean floor： new evidence［J］. Science， 1966， 154（3 755）： 1 405-1 415.

[4]
RAFF A D， MASON R G. Magnetic survey off the west coast of North America， 40°N. latitude to 52°N. latitude［J］. Geological Society of America Bulletin， 1961， 72（8）. DOI：10.1130/0016-7606（1961）72 ［1267：MSOTWC］2.0.CO；2.

[5]
MASON R G， RAFF A D. Magnetic survey off the west coast of North America， 32°N. latitude to 42°N. latitude［J］. Geological Society of America Bulletin， 1961， 72（8）. DOI：10.1130/0016-7606（1961）72 ［1259：MSOTWC］2.0.CO；2.

[6]
VINE F J， MATTHEWS D H. Magnetic anomalies over oceanic ridges［J］. Nature， 1963， 199（4 897）： 947-949.

[7]
LI Yuanjie， WEI Dongping. A comprehensive review of marine magnetic anomaly stripes［J］. Progress in Geophysics， 2016， 31（3）： 949-959.

李园洁，魏东平.海底磁异常条带研究综述［J］.地球物理学进展，2016， 31（3）： 949-959.

[8]
BUKRY D， BRAMLETTE M N. Coccolith age determinations leg 3， deep sea drilling project［R］ Initial reports of the deep sea drilling project， 3. U.S. Government Printing Office， 1970.

[9]
HONSHO C， URA T， KIM K， et al. Postcaldera volcanism and hydrothermal activity revealed by autonomous underwater vehicle surveys in Myojin Knoll caldera， Izu-Ogasawara arc［J］. Journal of Geophysical Research： Solid Earth， 2016， 121（6）： 4 085-4 102.

[10]
WU S， THORAM S， SUN J， et al. Characterizing marine magnetic anomalies： a machine learning approach to advancing the understanding of oceanic crust formation［J］. Journal of Geophysical Research： Solid Earth， 2025， 130（2）. DOI： 10.1029/2024JB030682 .

[11]
HARSHVARDHAN G， GOURISARIA M K， PANDEY M， et al. A comprehensive survey and analysis of generative models in machine learning［J］. Computer Science Review， 2020， 38. DOI：10.1016/j.cosrev.2020.100285 .

[12]
LECUN Y， BENGIO Y， HINTON G. Deep learning［J］. Nature， 2015， 521（7 553）： 436-444.

[13]
MENDEL V， MUNSCHY M， SAUTER D. MODMAG， a MATLAB program to model marine magnetic anomalies［J］. Computers & Geosciences， 2005， 31（5）： 589-597.

[14]
SCHETTINO A. Magan： a new approach to the analysis and interpretation of marine magnetic anomalies［J］. Computers & Geosciences， 2012， 39： 135-144.

[15]
IVANOV S A， MERKUR’EV S A. Interpretation of marine magnetic anomalies. part I. a survey of existing methods and analysis of the analytic signal method［J］. Geomagnetism and Aeronomy， 2014， 54（3）： 388-396.

[16]
IVANOV S A， MERKUR’EV S A. Interpretation of marine magnetic anomalies. part II. analysis of the new method and algorithm based on the least squares method［J］. Geomagnetism and Aeronomy， 2014， 54（4）： 530-536.

[17]
MEYER B， CHULLIAT A， SALTUS R. Derivation and error analysis of the Earth magnetic anomaly grid at 2 arc Min resolution version 3 （EMAG2v3）［J］. Geochemistry， Geophysics， Geosystems， 2017， 18（12）： 4 522-4 537.

[18]
DYER L. Identifying marine magnetic anomalies using machine learning［D］. Kent： Kent State University， 2022.

[19]
WANG S G， ZHANG X Y， QIN Y Q， et al. Marine target magnetic anomaly detection based on multitask deep transfer learning［J］. IEEE Geoscience and Remote Sensing Letters， 2023， 20. DOI： 10.1109/LGRS.2023.3273722 .

[20]
WANG C， PENG G， WANG H， et al. Multi-feature fusion and intelligent iterative optimization algorithm based magnetic anomaly detecting method， involves inputting magnetic signal sample into magnetic anomaly detection model to obtain magnetic anomaly detection result ［P］. 2021， CN112633147-A.

[21]
SAGER W W， KIM J， KLAUS A， et al. Bathymetry of shatsky rise， northwest Pacific Ocean： implications for ocean plateau development at a triple junction［J］. Journal of Geophysical Research： Solid Earth， 1999， 104（B4）： 7 557-7 576.

[22]
ZHANG J C， SAGER W W， KORENAGA J. The seismic Moho structure of Shatsky Rise oceanic plateau， northwest Pacific Ocean［J］. Earth and Planetary Science Letters， 2016， 441： 143-154.

[23]
ZHANG Jinchang， LUO Yiming， LI Haiyong， et al. Internal structure and evolutionary mechanisms of west Pacific oceanic plateaus［J］. Science & Technology Review， 2023，41（2）： 65-79.

张锦昌，罗怡鸣，李海勇，等.西太平洋洋底高原内部结构与形成演化［J］.科技导报， 2023， 41（2）： 65-79.

[24]
HUANG Y M， SAGER W， ZHANG J C， et al. Magnetic anomaly map of shatsky rise and its implications for oceanic plateau formation［J］. Journal of Geophysical Research： Solid Earth， 2018. DOI： 10.1029/2019JB019116 .

[25]
THORAM S， SAGER W W， REED W， et al. Improved high-resolution bathymetry map of Tamu massif and southern shatsky rise and its geologic implications［J］. Journal of Geophysical Research： Solid Earth， 2022， 127（11）. DOI： 10.1029/2022JB024304 .

[26]
HUANG Y M， SAGER W W， TOMINAGA M， et al. Magnetic anomaly map of Ori Massif and its implications for oceanic plateau formation［J］. Earth and Planetary Science Letters， 2018， 501： 46-55.

[27]
SAGER W W， HUANG Y M， TOMINAGA M， et al. Oceanic plateau formation by seafloor spreading implied by Tamu Massif magnetic anomalies［J］. Nature Geoscience， 2019， 12： 661-666.

[28]
SAGER W W， ZHANG J C， KORENAGA J， et al. An immense shield volcano within the Shatsky Rise oceanic plateau， northwest Pacific Ocean［J］. Nature Geoscience， 2013， 6（11）： 976-981.

[29]
NAKANISHI M， SAGER W W， KLAUS A. Magnetic lineations within shatsky rise， northwest Pacific Ocean： implications for hot spot-triple junction interaction and oceanic plateau formation［J］. Journal of Geophysical Research： Solid Earth， 1999， 104（B4）： 7 539-7 556.

[30]
NAKANISHI M， TAMAKI K， KOBAYASHI K. Mesozoic magnetic anomaly lineations and seafloor spreading history of the northwestern Pacific［J］. Journal of Geophysical Research： Solid Earth， 1989， 94（B11）： 15 437-15 462.

[31]
NAKANISHI M， TAMAKI K， KOBAYASHI K. Magnetic anomaly lineations from Late Jurassic to Early Cretaceous in the west-central Pacific Ocean［J］. Geophysical Journal International， 1992， 109（3）： 701-719.

[32]
TOMINAGA M， SAGER W W， TIVEY M A， et al. Deep-tow magnetic anomaly study of the Pacific Jurassic Quiet Zone and implications for the geomagnetic polarity reversal timescale and geomagnetic field behavior［J］. Journal of Geophysical Research： Solid Earth， 2008， 113（B7）. DOI： 10.1029/2007JB005527 .

[33]
KOPPERS A A P， STAUDIGEL H， WIJBRANS J R， et al. The Magellan seamount trail： implications for Cretaceous hotspot volcanism and absolute Pacific plate motion［J］. Earth and Planetary Science Letters， 1998， 163（1/2/3/4）： 53-68.

[34]
ZHAO Guochun， ZHANG Guowei. Origin of continents［J］. Acta Geologica Sinica， 2021， 95（1）： 1-19.

赵国春， 张国伟. 大陆的起源［J］. 地质学报， 2021， 95（1）： 1-19.

[35]
ZHANG X B， BROWN E L， ZHANG J C， et al. Magmatism of Shatsky Rise controlled by plume-ridge interaction［J］. Nature Geoscience， 2023， 16（11）： 1 061-1 069.

[36]
MEYER B， SALTUS R， CHULLIAT A. EMAG2v3： Earth magnetic anomaly grid （2-arc-minute resolution） Version 3 ［DS］. NOAA National Centers for Environmental Information， 2017.

[37]
RONNEBERGER O， FISCHER P， BROX T. U-Net： convolutional networks for biomedical image segmentation［M］// Medical image computing and computer-assisted intervention-MICCAI 2015. Cham： Springer International Publishing， 2015： 234-241.

[38]
WANG F， JIANG M Q， QIAN C， et al. Residual attention network for image classification［C］// 2017 IEEE conference on Computer Vision and Pattern Recognition （CVPR）. Honolulu， HI， USA： IEEE， 2017： 6 450-6 458.

[39]
CANNY J. A computational approach to edge detection［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1986， PAMI-8（6）： 679-698.

[40]
BARASH G， CASTILLO-EFFEN M， CHHAYA N， et al. Reports of the Workshops Held at the 2019 AAAI Conference on Artificial Intelligence ［R］. AI Magazine， 2019， 40（3）.

[41]
YANG B， BENDER G， LE Q V， et al. CondConv： conditionally parameterized convolutions for efficient Inference 33rd Conference on Neural Information Processing Systems ［C］. Vancouver， Canada， 2019.

[42]
ESTEVES C， SLOTINE J J， MAKADIA A. Scaling spherical CNNs［C］. 40th International Conference on Machine Learning， 2023.

Options
Outlines

/

〈 〉

Address: No. 8, Tianshui Middle Road, Lanzhou, Gansu
QQ：114723517
Tel：0931-8762293　E-mail：adearth@lzb.ac.cn
陇ICP备2021001824号-5　 甘公网安备62010202000687