

Received date: 2022-01-12
Revised date: 2022-06-16
Online published: 2022-07-21
Supported by
the Chinese Academy 100-Talent Program “Numerical hydrological model”(E0290304);The National Natural Science Foundation of China “The evolution of hydrological cycle and its mechanism under the climate change on the Sanjiangyuan region in China”(41930759);The Open Fund of Qinghai Key Laboratory of Disaster Prevention “Streamflow change and hydrological mechanism in Buha River”(QFZ-2021-Z02)
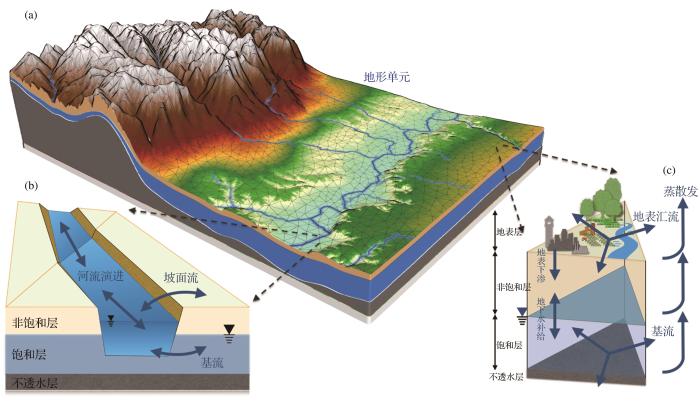
Hydrological models are efficient and economical tools for conducting scientific studies. They are not only useful in validating scientific theories and guiding the deployment of observation networks, but they also play an indispensable role in facilitating decision-making within socioeconomic spheres such disaster prevention and mitigation. Distributed hydrological modelling via numerical methods entail the application of hydrological equations to express the spatial heterogeneity of hydrological parameters at a fine-scale. This fine-scale analysis allows for a detailed characterization of hydrological processes, which is a critical step within the context of developing robust hydrological models. The SHUD model adopts the finite volume method to resolve integrated surface-subsurface hydrological processes. The model uses an irregular triangular network, which can rapidly realize an ultra-high-resolution numerical simulation (i.e., from meters to kilometers). The AutoSHUD automated hydrological simulation system, which consists of the SHUD model, rSHUD tool, and global essential terrestrial data, can facilitate pre- and post-processing of the model and has been applied to several research projects; hence, the validity and applicability of the model have been verified. At present, the exploration, development, and application of distributed hydrological models by numerical methods are limited in our hydrological community, and there is an urgent need for more original research in this field. The global development of new models as well as the validation, promotion, and improvement of existing models is a worthwhile goal.
Key words: Hydrological model; Distributed model; Numerical method; SHUD model
Lele SHU , Yan CHANG , Jian WANG , Hao CHEN , Zhaoguo LI , Lin ZHAO , Xianhong MENG . A Brief Review of Numerical Distributed Hydrological Model SHUD[J]. Advances in Earth Science, 2022 , 37(7) : 680 -691 . DOI: 10.11867/j.issn.1001-8166.2022.025
| 1 | BEVEN K. Rainfall-Runoff modelling: the primer [M]. second edition. Chichester, UK: John Wiley & Sons, Inc., 2012. |
| 2 | XU Zongxue. Hydrological models[M].Beijing:Science Press,2009. |
| 2 | 徐宗学.水文模型[M].北京:科学出版社,2009. |
| 3 | JIA Yangwen, WANG Hao, NI Guangheng. Principle and practice of distributed watershed hydrological model [M]. Beijing:China Water & Power Press,2005. |
| 3 | 贾仰文,王浩,倪广恒.分布式流域水文模型原理与实践[M].北京:中国水利水电出版社,2005. |
| 4 | PEEL M C, MCMAHON T A. Historical development of rainfall-runoff modeling[J]. Wiley Interdisciplinary Reviews: Water, 2020, 7(5): e1471. |
| 5 | CLARK M P, KAVETSKI D, FENICIA F. Pursuing the method of multiple working hypotheses for hydrological modeling[J]. Water Resources Research, 2011, 47(9): W09301. |
| 6 | HRACHOWITZ M, CLARK M P. HESS opinions: the complementary merits of competing modelling philosophies in hydrology[J]. Hydrology and Earth System Sciences, 2017, 21(8): 3 953-3 973. |
| 7 | THOMPSON S E, SIVAPALAN M, HARMAN C J, et al. Developing predictive insight into changing water systems: use-inspired hydrologic science for the Anthropocene[J]. Hydrology and Earth System Sciences, 2013, 17(12): 5 013-5 039. |
| 8 | PANICONI C, PUTTI M. Physically based modeling in catchment hydrology at 50: survey and outlook[J]. Water Resources Research, 2015, 51(9): 7 090-7 129. |
| 9 | MAXWELL R M, CONDON L E, KOLLET S J. A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3[J]. Geoscientific Model Development, 2015, 8(3): 923-937. |
| 10 | VALLIS G K. Geophysical fluid dynamics: whence,whither and why?[J]. Proceedings of the Royal Society A—Mathematical Physical and Engineering Sciences,2016,472(2 192):20160140. |
| 11 | SIVAPALAN M, BL?SCHL G. Time scale interactions and the coevolution of humans and water[J]. Water Resources Research,2015,51(9): 6 988-7 022. |
| 12 | SHEN C P, PHANIKUMAR M S. A process-based,distributed hydrologic model based on a large-scale method for surface-subsurface coupling[J]. Advances in Water Resources,2010,33(12): 1 524-1 541. |
| 13 | HAQUE A, SALAMA A, LO K, et al. Surface and groundwater interactions: a review of coupling strategies in detailed domain models[J]. Hydrology, 2021, 8(1): 35. |
| 14 | FREEZE R A, HARLAN R L. Blueprint for a physically-based, digitally-simulated hydrologic response model[J]. Journal of Hydrology, 1969, 9(3): 237-258. |
| 15 | MAXWELL R M, PUTTI M, MEYERHOFF S, et al. Surface-subsurface model intercomparison: a first set of benchmark results to diagnose integrated hydrology and feedbacks[J]. Water Resources Research, 2014, 50(2): 1 531-1 549. |
| 16 | QU Y Z, DUFFY C J. A semidiscrete finite volume formulation for multiprocess watershed simulation[J]. Water Resources Research, 2007, 43(8): W08419. |
| 17 | BIXIO A C, GAMBOLATI G, PANICONI C, et al. Modeling groundwater-surface water interactions including effects of morphogenetic depressions in the Chernobyl exclusion zone[J]. Environmental Geology, 2002, 42(2/3): 162-177. |
| 18 | AQUANTY I. HydroGeoSphere user manual[R]. Waterloo,Ontario, 2013. |
| 19 | DELFS J O, PARK C H, KOLDITZ O. A sensitivity analysis of Hortonian flow[J]. Advances in Water Resources, 2009, 32(9): 1 386-1 395. |
| 20 | KOLLET S J, MAXWELL R M. Integrated surface-groundwater flow modeling: a free-surface overland flow boundary condition in a parallel groundwater flow model[J]. Advances in Water Resources, 2006, 29(7): 945-958. |
| 21 | IVANOV V Y, VIVONI E R, BRAS R L, et al. Catchment hydrologic response with a fully distributed triangulated irregular network model[J]. Water Resources Research, 2004, 40(11): W11102. |
| 22 | REFSGAARD J C, STORM B. MIKE SHE[G]// Computer models of watershed hydrology. 1995: 809-846. |
| 23 | REFSGAARD J C. Parameterisation, calibration and validation of distributed hydrological models[J]. Journal of Hydrology, 1997, 198(1/2/3/4): 69-97. |
| 24 | SHU L L, ULLRICH P A, DUFFY C J. Simulator for Hydrologic Unstructured Domains (SHUD v1.0): numerical modeling of watershed hydrology with the finite volume method[J]. Geoscientific Model Development, 2020, 13(6): 2 743-2 762. |
| 25 | DUFFY C J. A two-state integral-balance model for soil moisture and groundwater dynamics in complex terrain[J]. Water Resources Research, 1996, 32(8): 2 421-2 434. |
| 26 | COBOURN K M, CAREY C C, BOYLE K J,et al. From concept to practice to policy: modeling coupled natural and human systems in lake catchments[J]. Ecosphere,2018,9(5):e02209. |
| 27 | WARD N K, FITCHETT L, HART J A, et al. Integrating fast and slow processes is essential for simulating human-freshwater interactions[J]. Ambio, 2019, 48(10): 1 169-1 182. |
| 28 | GIL Y, GARIJO D, KHIDER D, et al. Artificial intelligence for modeling complex systems: taming the complexity of expert models to improve decision making[J]. ACM Transactions on Interactive Intelligent Systems, 2021, 11(2): 1-49. |
| 29 | GARIJO D, KHIDER D, RATNAKAR V,et al. An intelligent interface for integrating climate,hydrology,agriculture,and socioeconomic models[C]// Proceedings of the 24th international conference on intelligent user interfaces: companion. New York,NY,USA: Association for Computing Machinery,2019:111-112. |
| 30 | LADWIG R, HANSON P C, DUGAN H A, et al. Lake thermal structure drives interannual variability in summer Gnoxia dynamics in a eutrophic lake over 37 years[J]. Hydrology and Earth System Sciences, 2021, 25(2): 1 009-1 032. |
| 31 | KOLLET S, SULIS M, MAXWELL R M, et al. The integrated hydrologic model intercomparison project, IH-MIP2: a second set of benchmark results to diagnose integrated hydrology and feedbacks[J]. Water Resources Research, 2017, 53(1): 867-890. |
| 32 | BROWN P N, HINDMARSH A C. Reduced storage matrix methods in stiff ODE systems[J]. Applied Mathematics and Computation, 1989, 31: 40-91. |
| 33 | COURANT R, FRIEDRICHS K, LEWY H. über die partiellen differenzengleichungen der mathematischen physik[J]. Mathematische Annalen, 1928, 100(1): 32-74. |
| 34 | ARNOLD J G, FOHRER N. SWAT2000: current capabilities and research opportunities in applied watershed modelling[J]. Hydrological Processes, 2005, 19(3): 563-572. |
| 35 | SHI Y N, DAVIS K J, DUFFY C J, et al. Development of a coupled land surface hydrologic model and evaluation at a critical zone observatory[J]. Journal of Hydrometeorology, 2013, 14(5): 1 401-1 420. |
| 36 | SHI Y N, BALDWIN D C, DAVIS K J, et al. Simulating high-resolution soil moisture patterns in the Shale Hills watershed using a land surface hydrologic model[J]. Hydrological Processes, 2015, 29(21): 4 624-4 637. |
| 37 | BAO C, LI L, SHI Y N, et al. Understanding watershed hydrogeochemistry: 1. development of RT-flux-PIHM[J]. Water Resources Research, 2017, 53(3): 2 328-2 345. |
| 38 | LI L, BAO C, SULLIVAN P L, et al. Understanding watershed hydrogeochemistry: 2. synchronized hydrological and geochemical processes drive stream chemostatic behavior[J]. Water Resources Research, 2017, 53(3): 2 346-2 367. |
| 39 | YU X, XU Z X, MORAETIS D, et al. Capturing hotspots of fresh submarine groundwater discharge using a coupled surface-subsurface model[J]. Journal of Hydrology, 2021, 598: 126356. |
| 40 | ZHANG Y, SLINGERLAND R, DUFFY C. Fully-coupled hydrologic processes for modeling landscape evolution[J]. Environmental Modelling & Software, 2016, 82: 89-107. |
| 41 | SHI Y N, EISSENSTAT D M, HE Y T, et al. Using a spatially-distributed hydrologic biogeochemistry model with a nitrogen transport module to study the spatial variation of carbon processes in a critical zone observatory[J]. Ecological Modelling, 2018, 380: 8-21. |
| 42 | VAUCLIN M, KHANJI D, VACHAUD G. Experimental and numerical study of a transient, two-dimensional unsaturated-saturated water table recharge problem[J]. Water Resources Research, 1979, 15(5): 1 089-1 101. |
| 43 | W?STEN J H M, PACHEPSKY Y A, RAWLS W J. Pedotransfer functions: bridging the gap between available basic soil data and missing soil hydraulic characteristics[J]. Journal of Hydrology, 2001, 251(3/4): 123-150. |
| 44 | HANSEN N, OSTERMEIER A. Adapting arbitrary normal mutation distributions in evolution strategies: the covariance matrix adaptation[C]// Proceedings of IEEE international conference on evolutionary computation. IEEE,1996:312-317. |
| 45 | AUGER A, HANSEN N. A restart CMA evolution strategy with increasing population size[J]. IEEE Congress on Evolutionary Computation, 2005, 2: 1 769-1 776. |
| 46 | SHU L L. Impacts of urbanization and climate change on the hydrological cycle: a study in modern and ancient land use change[D]. Central County: The Pennsylvnia State University,2017. |
| 47 | DUAN S H, ULLRICH P, SHU L L. Using convolutional neural networks for streamflow projection in California[J]. Frontiers in Water, 2020, 2: 28. |
| 48 | KUFFOUR B N O, ENGDAHL N B, WOODWARD C S, et al. Simulating coupled surface-subsurface flows with ParFlow v3.5.0: capabilities, applications, and ongoing development of an open-source, massively parallel, integrated hydrologic model[J]. Geoscientific Model Development, 2020, 13(3): 1 373-1 397. |
| 49 | MAXWELL R M, MILLER N L. Development of a coupled land surface and groundwater model[J]. Journal of Hydrometeorology, 2005, 6(3): 233-247. |
| 50 | GILBERT J M, JEFFERSON J L, CONSTANTINE P G, et al. Global spatial sensitivity of runoff to subsurface permeability using the active subspace method[J]. Advances in Water Resources, 2016, 92: 30-42. |
/
| 〈 |
|
〉 |