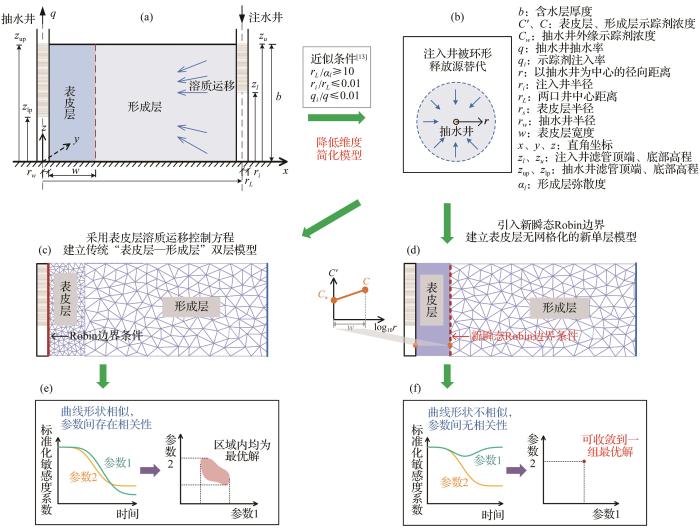
抽水井表皮层溶质运移控制方程受到异参同效的影响，存在参数估计的多解性问题。提出一个新的抽水井表皮层溶质运移方程（新瞬态Robin边界条件），并以径向收敛示踪试验为例构建其溶质运移模型。当抽水井为完整井时，通过拉普拉斯变换和有限傅立叶余弦变换得到模型的解析解；当抽水井为非完整井时，应用有限元法构建数值解。结果表明，表皮层溶质运移控制方程导致所估计的表皮层宽度（w）和形成层垂向弥散度（{\alpha }_z）是在0.5 m≤w≤1.0 m和0.08 m≤{\alpha }_z≤0.10 m范围内的任意组合，偏离实际值。反之，当表皮层佩克莱数（w和表皮层径向弥散度的比值）小于1时，新瞬态Robin边界条件能够准确反映表皮层的影响，消除w与{\alpha }_z的多解性。参数估计值（w=0.31 m、{\alpha }_z=0.17 m）唯一，接近实际值。新模型已成功用于野外试验。

The governing equation of solute transport in the well skin produces multiple parameter estimates because of the equifinality of modeling radially convergent tracer tests. A new transport equation for the skin of an extraction well (i.e., a new transient Robin boundary condition) is proposed. A new analytical model was developed to test a fully penetrating extraction well. The analytical solution of the model was obtained using the Laplace transform and finite Fourier cosine transform. A finite element solution was acquired for the test in a partially penetrating extraction well. Results suggest the skin governing equation produces the estimates of the skin width w and formation vertical dispersivity α_z are arbitrary values chosen from the ranges of 0.5 m≤w≤1 m and 0.08 m≤α_z ≤0.1 m. These ranges exclude the default values. In contrast, the new Robin boundary condition accurately reflects the skin effect when the Peclet number, defined as the ratio of w to the longitudinal dispersivity of the skin, is less than 1. The present solution relying on this boundary condition predicts the single optimal estimates of w and α_z . The estimates (w=0.31 m, α_z =0.17 m) approach their default values. The present solution applies to field tests.