地球科学进展

地球科学进展, 2019, 34(4): 414-423 DOI: 10.11867/j.issn.1001-8166.2019.04.0414

地球化学

水热体系中Na2SO4/K2SO4溶解度的热力学计算

张为,1,2, 周丽,2, 唐红峰2, 李和平2, 王力2,3

1. 贵州师范大学喀斯特生态文明研究中心，贵州 贵阳 550025

2. 中国科学院地球化学研究所地球内部物质高温高压院重点实验室，贵州 贵阳 550002

3. 中国科学院大学，北京 100039

Thermodynamic Calculation of Solubility of Na2SO4/K2SO4 in Hydrothermal Fluids

Zhang Wei,1,2, Zhou Li,2, Tang Hongfeng2, Li Heping2, Wang Li2,3

1. Research Center of Karst Ecological Civilization, Guizhou Normal University, Guiyang 550025, China

2. Key Laboratory of High-Temperature and High-Pressure Study of the Earth’s Interior, Institute of Geochemistry, Chinese Academy of Sciences, Guiyang 550002, China

3. University of Chinese Academy of Sciences, Beijing 100039, China

通讯作者: 周丽（1980-），男，湖北潜江人，副研究员，主要从事高温高压实验地球化学研究. E-mail：zhouli@vip.gyig.ac.cn

收稿日期: 2018-11-08   修回日期: 2019-03-19   网络出版日期: 2019-05-22

基金资助: 国家自然科学基金项目“独居石和磷钇矿在热液中溶解行为的实验研究：对U-Th-Pb年龄有效性以及稀土元素成矿的约束”.  编号：41773058
贵州省科技厅—贵州师范大学联合基金项目“石阡县地热资源可持续利用研究”.  编号：黔科合LH字[2017]7339号

Corresponding authors: Zhou Li (1980-), male, Qianjiang City, Hubei Province, Associate professor. Research areas include experimental geochemistry at high-temperature and high pressure. E-mail：zhouli@vip.gyig.ac.cn

Received: 2018-11-08   Revised: 2019-03-19   Online: 2019-05-22

作者简介 About authors

张为（1988-），男，湖北武汉人，讲师，主要从事水—岩反应相关的地球化学研究.E-mail：zhangwei@gznu.edu.cn

ZhangWei(1988-),male,WuhanCity,HubeiProvince,Lecturer.Researchareasincludeexperimentalandcomputationalgeochemistryonwater-rockreactions.E-mail:zhangwei@gznu.edu.cn

摘要

硫酸盐流体是自然界中的常见热液，其盐度可以为成矿流体演化、成矿元素的迁移富集和矿床类型的划分等提供重要信息。但是现有文献报道的Na2SO4和K2SO4溶解度多是在饱和蒸气压条件或超临界条件下，而对于低温成矿热液体系的实验研究较少。热力学计算是研究流体性质的重要手段，特别是在实验结果较少的温压范围内起着重要作用，但是利用热力学模型来计算硫酸盐溶解度的工作却少有开展。使用Pitzer模型，利用Na2SO4和K2SO4溶液高温高压条件下的密度数据，使用非线性最小二乘法拟合，获得了压力对Na2SO4和K2SO4的活度系数及其溶解过程中的标准偏摩尔体积影响的模型参数，评价了压力对其活度系数和标准偏摩尔体积的影响。结合文献中饱和蒸气压下的相关参数，构建了温度范围为0~250 oC，压力范围为0.1~40.0 MPa，Na2SO4和K2SO4溶解度的热力学计算模型。模型计算结果与文献数据吻合较好。计算结果还显示，压力对Na2SO4和K2SO4的平均活度系数和溶度积都有正向的促进作用，但是由于平均活度系数随压力的变化更大，导致Na2SO4和K2SO4的溶解度随压力的增大而降低，并且随着温度的升高这种降低的程度变得更大。

关键词： 硫酸盐流体包裹体 ; 溶解度 ; 热力学计算 ; Pitzer模型

Abstract

Sulfate fluids are common fluids in nature, and their salinity studies can provide important information for the evolution of ore-forming fluids, migration and enrichment of ore-forming elements, and the classification of deposit types. Considerable research has been carried out to investigate the solubility of Na2SO4 and K2SO4 in hydrothermal fluids, however most of the literature reported experimental data were under saturated vapor pressure or the water supercritical region. A few data have been reported for the low temperature hydrothermal mineralization region. Thermodynamic model is a useful method to study the properties of hydrothermal geofluids, especially for mineral solubility. Pitzer interaction model is one of the most widely used model to calculate the thermodynamic properties of hydrothermal fluids, but few work have ever been carried out to calculate the solubility of sulfate at high temperature and pressure. With Pitzer specific interaction model, using the literature reported density data of Na2SO4 and K2SO4 solutions at high temperature and pressure, the pressure effect on Pitzer activity coefficient of sulfate and the standard partial molar volume change during sulfate dissolution process were evaluated and related parameters were obtained. The standard partial molar volumes of Na2SO4 and K2SO4 calculated with these parameters agreed well with those reported in the literature. Combined with the relevant parameters in the literature under saturated vapor pressure, a thermodynamic model for Na2SO4 and K2SO4 solubility calculation with temperature up to 250 ℃ and pressure up to 40 MPa was developed. The model gave very good agreement with the experimental solubility data. With this model, Na2SO4 and K2SO4 solubility was calculated at high temperature and pressure. The calculation results showed that pressure had a positive effect on both the average activity coefficient and solubility product of Na2SO4 and K2SO4, but the solubility of Na2SO4 and K2SO4 decreased with pressure due to the larger change of the average activity coefficient with pressure. And as the temperature increased, the degree of such reduction became larger. The results herein can provide instructions for the compositional analysis of sulfate fluid inclusions.

Keywords： Sulfate fluids inclusion ; Solubility ; Thermodynamic model ; Pitzer model.

PDF (1599KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张为, 周丽, 唐红峰, 李和平, 王力. 水热体系中Na2SO4/K2SO4溶解度的热力学计算. 地球科学进展[J], 2019, 34(4): 414-423 DOI:10.11867/j.issn.1001-8166.2019.04.0414

Zhang Wei, Zhou Li, Tang Hongfeng, Li Heping, Wang Li. Thermodynamic Calculation of Solubility of Na2SO4/K2SO4 in Hydrothermal Fluids. Advances in Earth Science[J], 2019, 34(4): 414-423 DOI:10.11867/j.issn.1001-8166.2019.04.0414

1 引 言

硫酸盐流体是地质流体的一个重要类型，在海陆相各环境中广泛存在[1]，在四川冕宁木落稀土矿床[2]、兰坪金顶超大型铅锌矿床[3]和河南省大河沟锑矿[4]都有发现。流体包裹体是圈闭在矿物晶格缺陷，或其窝穴中保存下来的古流体，是成岩成矿流体的最直观体现[5]。流体包裹体的一项重要研究内容是包裹体盐度的确定[6,7,8,9]，成矿热液中硫酸盐（Na2SO4/K2SO4）溶解度的研究，对反映成矿流体演化过程[10]、矿床类型的划分[11]、流体的氧化还原状态[12]和成矿元素的迁移富集规律[13]具有重要的指示意义。

水热体系中Na2SO4/K2SO4溶解度的研究已经取得了很多非常重要的成果，但是大部分实验数据的温度范围都是在100 oC以内[14]，温度在100 oC以上的数据也多是在饱和蒸汽压条件下[15,16]。另外，由于Na2SO4/K2SO4等无机超临界流体的特殊性质，化学家们研究了超临界条件下（温度≥374 oC、压力≥22 MPa）Na2SO4和K2SO4的溶解度，并给出了计算其溶解度的相关经验模型[17,18,19]。但是对于温度≤250 oC的低温热液矿床内的硫酸盐流体性质的研究很少。

热力学计算是模拟物质迁移转化、成矿流体演化，及成矿流体热力学性质最常用也是最强有力的工具之一[20,21,22,23]，特别是在实验结果较少的温压范围内起着重要的作用，且在H2O，NaCl-H2O以及NaCl-H2O-CO2流体热力学性质方面已经取得了丰硕的成果[24,25]。Greenberg等[26]和Pabalan等[27]总结了文献中Na2SO4和K2SO4体系的溶解度等热力学数据，利用Pitzer模型建立了0~250 oC，饱和蒸汽压下Na2SO4和K2SO4溶解度计算模型，但是对于更高压力条件下硫酸盐溶解度的研究还很少。因此，本文拟通过热力学计算研究低温热液水热体系中Na2SO4和K2SO4的溶解度，力图为低温成矿热液中硫酸盐流体包裹体盐度的研究提供一定的指导。

2 理论背景及计算方法

水热体系中Na2SO4和K2SO4的溶解过程可表示为：

Na2SO4(s)↔2Na++SO42- ，
K2SO4(s)↔2K++SO42- ，

与之对应的溶解平衡反应为：

KNa2SO4=aNa+2∙aSO42-=mNaγNa2∙(mSO42-γSO42-) ，
KK2SO4=aK+2∙aSO42-=mKγK2∙(mSO42-γSO42-) ，

式中：KNa2SO4（或KK2SO4）表示硫酸盐的溶解平衡常数；ai，mi和γi（i表示Na+，K+和SO42-）分别表示溶液中物种的活度、质量摩尔浓度和活度系数。为了描述水热体系中Na2SO4和K2SO4的溶解度，就需要同时获得矿物溶解的溶解平衡常数（Ksp）和相关物种的活度系数（γ）。

Pitzer[28]模型被广泛应用于水热体系中物质活度系数的计算[29]，被PHREEQC[30]，GEM-Selektor[31]和ScaleSoftPitzer[32]等世界知名的地球化学计算软件所采用。Greenberg等[26]利用Pitzer模型建立了0~250 oC，饱和蒸气压下Na2SO4和K2SO4的溶解度计算模型。但是，Shi等[33]发现不考虑压力情况下重晶石的溶解度要比实验结果低27%，为了准确描述矿物在高温高压下的溶解度就必须考虑压力对活度系数和溶解平衡常数的影响[34]。

2.1　压力对溶解平衡常数和活度系数的影响

溶解平衡常数随压力的变化可表示为[35,36,37]：

lnKspT,P=lnKspT,P0-∆rV0RTP-P0 ，

式中：KspT,P和KspT,P0分别为目标温度压力下和参考压力下的溶解平衡常数；P和T分别表示体系的压力和温度，P0表示参考压力，当温度低于100 oC时，P0=0.1 MPa；当温度高于100 oC时，P0表示水的饱和蒸汽压；R为理想气体常数；∆rV0是溶解反应过程中偏摩尔体积的变化。对于Na2SO4（或K2SO4）而言：

∆rV0=V0Na2SO4,aq-V0(Na2SO4,s) ，

式中：V0Na2SO4,aq是溶解反应生成物Na+和SO42-的标准偏摩尔体积之和，V0(Na2SO4,s)是固体Na2SO4（或K2SO4）的标准偏摩尔体积。25 oC和0.1 MPa时，Na2SO4和K2SO4的标准偏摩尔体积分别为53.33和65.5 cm3/mol [38]，且可以不考虑固体矿物的体积随温度压力的变化[37]。

依据Pitzer模型，高压下溶质的活度系数可依据饱和蒸汽压时的活度系数计算[39,40]：

lnγP=lnγPsat-AϕP-AϕPsat×I1+bI+2bln(1+bI)+2mβ0v+β1v(2/α2I)1-1+αI×exp-αIP-Psat+3m2Cv(P-Psat) ,

式中：γ(P)和γ(Psat)分别为目标压力和饱和蒸汽压下的活度系数；P和Psat分别为目标压力和饱和蒸汽压力；Aϕ是Debye-Hückel系数；m为溶质的质量摩尔浓度，I为溶液的离子强度；β0v，β1v和Cv分别表示Pitzer模型参数β0，β1和Cφ对压力的导数；α =2 kg1/2 ⋅ mol1/2， b = 1.2 kg1/2。

2.2　高温高压下溶解平衡常数和活度系数的计算

Pitzer模型表示的是物种的吉布斯自由能，经过适当的微分可以得到焓、热容和体积（密度）等性质。相反也可以利用热容、焓和密度等数据来评价温度、压力对模型参数的影响[41]。电解质溶液的密度可以用来计算压力对电解质的偏摩尔体积和Pitzer模型表示的溶质的活度系数的影响[20,40]。

电解质的表观摩尔体积可以表示为[36]：

V∅=1m(1000+mMsρsol-1000ρ0) ，

式中:V∅表示电解质的表观摩尔体积（apparent molar volume，cm3/mol）；m是电解质的质量摩尔浓度(mol/kg H2O)；Ms是电解质的摩尔质量(g/mol)；ρsol和ρ0分别为目标温度压力下溶液和纯水的密度(g/cm3)；其中纯水的密度依据IAPWS97方程来计算[42]。

结合Pitzer模型，电解质的表观摩尔体积可表示为：

V∅=V∅0+v|z+z-|Avln1+bI/2b+2v+v-mRT(Bv+v+z+mCv) ，
Bv=β0v+β1v(2/α2I)1-1+αI×exp-αI ，

式中：V∅0是电解质在无限稀溶液中的表观摩尔体积，即电解质的标准偏摩尔体积；Bv，β0v，β1v和Cv分别表示Pitzer参数模型参数压力的参数，且一般可以不考虑压力对β1v的影响[43]。z+和z-分别是阳离子和阴离子的电价，v+和v-分别是阳离子和阴离子的化学计量数，v = v+ + v-。Av是体积Debye-Hückel斜率，依据Bradley等[44]的工作计算得出。I是溶液的离子强度，R = 8.314 cm3·MPa/（K·mol）。

由于电解质的标准偏摩尔体积V∅0随温度快速变化，因此一般采用参考浓度法间接确定其随温度压力的变化情况[45,46]。

依据公式（9），参考浓度为mr时溶质的表观摩尔体积为：

V∅,mr=V∅0+v|z+z-|Avln1+bImr/2b+2v+v-mrRT(β0v+v+z+mrCv) 。

将公式（9）减去公式（11），就可以用参考浓度为mr时的表观摩尔体积表示任意浓度下溶液的表观摩尔体积：

V∅,m=V∅,mr+v|z+z-|Avln1+bIm/2b-ln1+bImr/2b+2v+v-RTβ0vm-mr+z+v+Cvm2-mr2 。

将公式（8）代入到公式（12）中，则：

1000+mMsmρsol-1000mρ0
=Vmrmr-1000mrρ0+v|z+z-|Avln1+bIm/2b
-ln1+bImr/2b+2v+v-RTβ0vm-mr
+z+v+Cvm2-mr2 ，

式中：参考浓度mr一般选用参与参数拟合的实验数据中浓度的上限值，V(mr)，β0v和Cv是温度和压力的函数；ρsol和ρ0分别为目标温度压力下溶液和纯水的密度；Av，b，β0v等表示的意义如以上所述。同时，利用公式（11）可以反向计算电解质溶液的标准偏摩尔体积：

V∅0=Vmrmr-1000mrρ0-v|z+z-|Avln1+bImr/2b-2v+v-mrRT(β0v+v+z+mrCv) ，

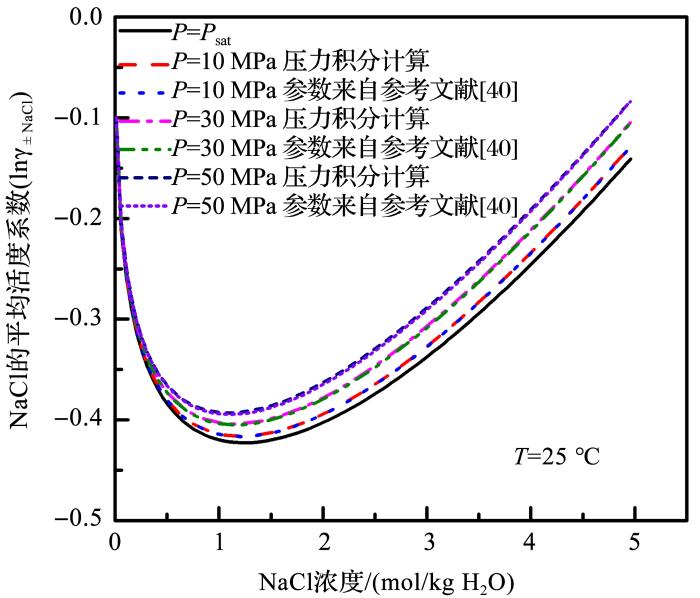
通过以上过程，利用水热体系中电解质溶液的密度数据，可以拟合获得V(mr)，β0v和Cv等参数，依据公式（7）可以评价压力对溶质活度系数的影响，利用公式（14）计算的溶质标准偏摩尔体积和公式（5）可以计算溶质的溶解反应平衡常数随压力的变化，进而依据公式（3）和（4）计算得到水热体系中电解质的溶解度。

Pitzer等[40]利用水热体系中NaCl溶液的热容和焓等热力学数据确定了0~300 oC，0.1~100.0 MPa，0~6 m范围内NaCl活度系数。Møller[47]确定了0~250 oC，饱和蒸气压下NaCl的活度系数参数；Mao等[25]利用Pitzer模型确定了水热体系中NaCl标准偏摩尔体积和压力对Pitzer参数影响的参数，将二者结合利用公式（7），我们计算了水热体系中NaCl的平均活度系数（图1）。从图1可看出，结合饱和蒸汽压下参数与压力积分项计算出来的不同浓度下NaCl的平均活度系数和Pitzer等[40]完整模型参数计算出来的结果吻合得很好，证明了该方法和计算过程的可行性。从图1还可看出，在NaCl溶液体系中，压力对活度系数有较大的影响，活度系数随着压力的升高而增大。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   25 oC不同压力下，模型计算的NaCl的平均活度系数随浓度的变化

Fig. 1   The model calculated NaCl mean activity coefficient at 25 oC as a function of concentration under different pressure


3 高温高压条件下Na2SO4和K2SO4溶解度的计算

对于水热条件下Na2SO4体系的密度实验数据文献已有全面而详实的报道，超过1 000个实验数据跨越温度0~300.0 oC，压力0.1~80.0 MPa（表1）。关于K2SO4体系的密度数据相对较少（表2）。Obšil等[48]和Azizov[58]实验研究了20.0~300.0 oC，10.0~30.0 MPa条件下K2SO4溶液的密度；Ellis[53]和Saluja等[54]研究获得了0~200.0 oC，0.1~2.0 MPa条件下K2SO4溶液的密度。不同来源的K2SO4体系密度数据之间具有较好的一致性，其密度数据的跨度范围为0~300.0 oC，0.1~40.0 MPa。

表1   Na2SO4-H2O体系密度实验数据

Table 1  Summary of density data of Na2SO4-H2O system

温度范围/oC压力范围/MPa参考文献
25.0~300.09.0~30.0[48]
25.0~200.01.1~68.6[49]
5.0~60.00.1[50]
20.0~200.02.0~10.0[51]
0~50.00.1~80.0[52]
50.0~200.02.0[53]
25.0~100.00.6[54]
25.0~250.00.1~40[55]
30.0~300.02.4~39.8[56]
5.0~100.00.1[57]

新窗口打开| 下载CSV


表2   K2SO4-H2O体系密度的实验数据

Table 2  Summary of density data of K2SO4-H2O system

温度范围/oC压力范围/MPa参考文献
25.0~300.09.0~30.0[48]
50.0~200.02.0[53]
25.0~100.00.6[54]
0~90.00.1[57]
20.0~300.05.0~40.0[58]

新窗口打开| 下载CSV


对于Na2SO4和K2SO4体系，公式（9）和公式（14）转化为：

V∅=V∅0+6Avln1+bI/2b+4mRT(β0v+2mCv) ，
V∅0=V(mr)mr-1000mrρ0-6Avln1+bImr/2b-4RT(mrβ0v+2Cvmr2) 。

其中，参考浓度下的摩尔体积和Pitzer模型压力参数计算如下：

V(mr)=a1+a2T+a3T2+a4T3+(a5+a6T+a7T2)P ，
β0v=a8+a9T-227+a10T ，
Cv=a11+a12T-227+a13T ，

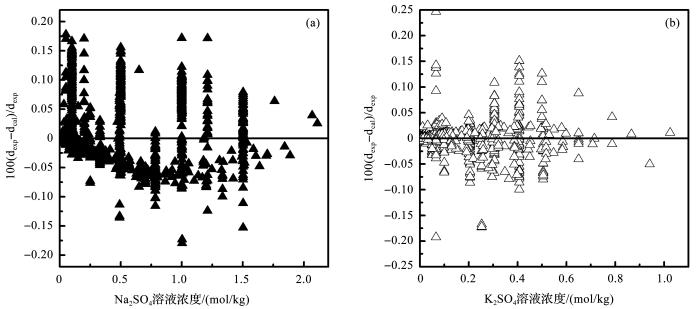
式中：T为开尔文温度；P表示体系的压力，单位为MPa；ai表示模型计算的参数。对于Na2SO4和K2SO4体系，利用表1和表2所列溶液的密度数据，采用非线性最小二乘法，同时拟合获得公式（17）~（19）的参数（表3）。拟合结果显示，在全部温度压力范围内，模型计算的溶液密度和实验结果的平均偏差分别是0.057%（Na2SO4）和0.047%（K2SO4），绝大部分实验数据和模型计算的偏差都在0.1%以内（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   水热体系中模型计算的Na2SO4溶液密度（a）和K2SO4溶液密度（b）与实验数据的对比

Fig.2   Plot of density deviations between model calculation and literature data of Na2SO4 + H2O (a)and K2SO4 + H2O (b) system


表3   Na2SO4和K2SO4体积性质计算的参数

Table 3  Parameters for the volumetric properties calculation of Na2SO4 and K2SO4

参数Na2SO4K2SO4
mr1.51.0
a19.69382688×1021.10686112×103
a22.83105828×10-1-5.98247606×10-1
a3-9.00393580×10-45.96259241×10-4
a42.57624184×10-62.39804594×10-6
a5-1.43199512×100-2.71085716×100
a67.37402186×10-31.41493666×10-2
a7-1.17539062×10-5-2.08587301×10-5
a8-4.86834961×10-45.43596750×10-3
a98.87142143×10-24.61245819×10-3
a102.75966178×10-7-1.21299746×10-5
a112.13350752×10-4-5.55380818×10-3
a12-1.36823713×10-26.41685688×10-2
a13-2.95936943×10-71.44544684×10-5

新窗口打开| 下载CSV


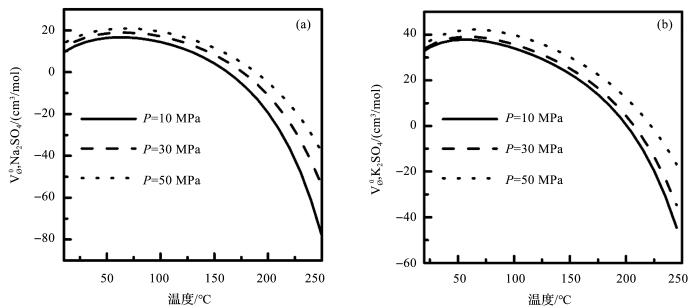
依据公式（16）和表3中的参数，我们计算不同温度压力条件下Na2SO4和K2SO4的标准偏摩尔体积。计算结果显示，25 ℃和0.1 MPa时，模型计算的Na2SO4和K2SO4的标准偏摩尔体积分别为12.26和33.42 cm3/mol，与实验测得的Na2SO4（12.09 cm3/mol）和K2SO4（33.70 cm3/mol）[59]的结果吻合得很好。与此同时，我们还计算了Na2SO4和K2SO4的标准偏摩尔体积随温度压力的变化（图3）。从图3可看出，Na2SO4和K2SO4的标准偏摩尔体积随温度强烈的变化，在整个温度范围内，随温度的升高而降低，随压力的增大而增大。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   Na2SO4（a）和K2SO4（b）标准偏摩尔体积随温度的变化

Fig.3   The standard partial molar volumes of Na2SO4(a) and K2SO4(b)against temperature and pressure


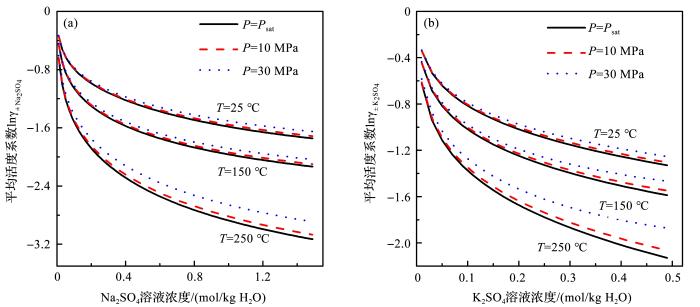
Greenberg等[26]确定了温度0~250 oC，饱和蒸汽压下Na2SO4和K2SO4活度系数随温度变化的参数。依据公式（7）和以上获得的参数，我们可以评价压力对Na2SO4和K2SO4活度系数的影响（图4）。从图4中可以看出，压力的增大会导致Na2SO4和K2SO4的平均活度系数的增大，并且随着溶液浓度的增大和温度的增高，这种增加的趋势更明显。对于Na2SO4体系，250 oC和30 MPa，1.5 m时Na2SO4的平均活度系数比相同温度浓度下，饱和蒸汽压时增加了0.02（图4a）；K2SO4体系中，250 oC和30 MPa， 0.5 m时的平均活度系数比饱和蒸汽压时增加了0.03（图4b）。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同温度压力下模型计算的Na2SO4（a）和K2SO4（b）平均活度系数随浓度的变化

Fig. 4   The model calculated Na2SO4(a) and K2SO4(b) mean activity coefficient as a function of concentration at different temperature and pressure


获得了压力对Na2SO4和K2SO4的标准摩尔体积和活度系数的影响之后，依据公式（4）和公式（5）计算了水热体系中Na2SO4和K2SO4的溶度积和溶解度。从表4可以看出，模型计算的结果和实验测得的溶解度之间吻合较好。对于Na2SO4体系，Voisin等[60]研究了压力为25 MPa时，水热体系中Na2SO4溶解度随温度的变化，并给出了计算Na2SO4溶解度的经验公式。从表4我们发现，本文模型计算的Na2SO4溶解度与Voisin等[60]经验公式计算的结果吻合较好。但是对于K2SO4体系，高压的实验数据基本都是在超临界条件以上，只能和饱和蒸汽压的实验室数据对比。

表4   模型计算的Na2SO4和K2SO4溶解度和实验结果的对比

Table 4  Comparison between model calculated Na2SO4 and K2SO4 with experimental data

温度/oC实验结果/（mol/kg）模型计算/（mol/kg）参考文献

Na2SO4

P=Psat

60.03.153.34[16,27]
100.02.993.04
120.02.952.94
140.72.962.89
200.73.153.16

K2SO4

P=Psat

50.000.950.94[15]
80.001.231.20
100.01.401.33
150.01.691.57
190.01.971.71

Na2SO4

P= 25 MPa

50.03.533.19[60]
100.02.342.74
150.02.332.53
180.02.392.48
200.02.412.46
220.02.372.40

新窗口打开| 下载CSV


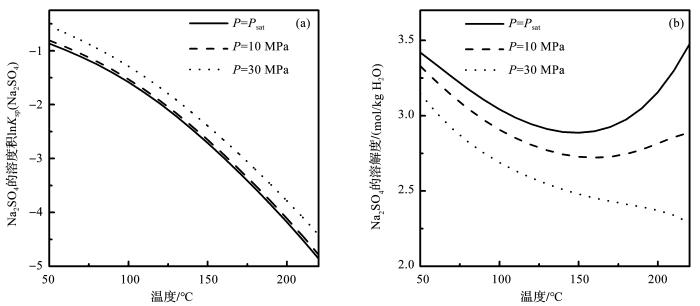
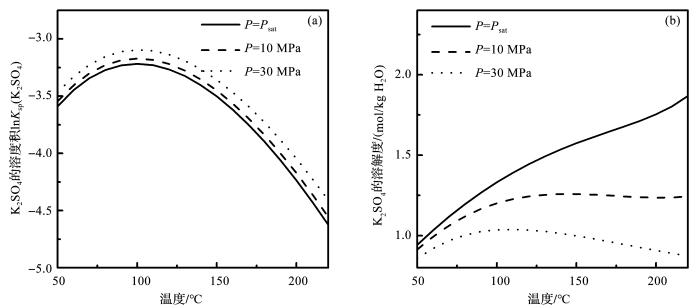
图5和图6分别表示水热体系模型计算的Na2SO4和K2SO4的溶度积的自然对数和溶解度。从图5a中可以看出，压力能够促进电解质溶解平衡常数的增加，在150 oC，压力为饱和蒸气压，10 MPa和30 MPa时，Na2SO4溶解平衡常数的自然对数分别为-2.71，-2.65和-2.55；相同条件下K2SO4溶度积的自然对数分别为-3.50，-3.45和-3.36（图6a）。但是压力对电解质溶解度的影响，却恰好与之相反。从图5b中可以看出，随着压力的增大，电解质的溶解度却迅速降低。150 oC时，随着压力的增加，Na2SO4的溶解度从饱和蒸气压的2.89 mol/kg降低到10 MPa的2.73 mol/kg，最后降低到30 MPa的2.48 mol/kg。在相同温压条件下，K2SO4的溶解度分别为1.57，1.26和1.00 mol/kg。随着温度的升高，溶解度的减少量更大（图6b）。这是因为压力对Na2SO4和K2SO4的溶度积和平均活度系数都有正向的促进作用，但是压力对Na2SO4和K2SO4平均活度系数的影响更明显，结果就导致了Na2SO4和K2SO4溶解度的降低。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   Na2SO4溶解平衡常数的自然对数（a）和溶解度（b）随温度压力的变化

Fig.5   The natural logarithm of Na2SO4 solubility product (a) and solubility (b) at different temperature and pressure


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   K2SO4溶解平衡常数的自然对数（a）和溶解度（b）随温度压力的变化

Fig.6   The natural logarithm of K2SO4 solubility product (a) and solubility (b) at different temperature and pressure


4 结 论

本文使用Pitzer模型，利用水热体系中Na2SO4和K2SO4溶液的密度数据，使用非线性最小二乘法拟合，获得了Pitzer模型表示的Na2SO4和K2SO4的活度系数以及Na2SO4(aq)和K2SO4(aq)的标准偏摩尔体积随压力变化的模型参数，评价了压力对Na2SO4和K2SO4的溶度积和活度系数的影响，结果显示压力对Na2SO4和K2SO4的平均活度系数和溶度积都有正向的促进作用，但是压力对活度系数的影响更大。在此基础上构建了温度到250 oC，压力到40 MPa的Na2SO4和K2SO4溶解度计算模型。模型计算的Na2SO4和K2SO4溶解度与已发表文献中的实验数据吻合较好。计算结果显示，Na2SO4和K2SO4的溶解度随压力的增大而降低，并且随着温度的升高降低的程度也变得更大。

参考文献

Xiao Rongge , Zhang Zongheng , Chen Huiquan , et al .

Types of geological fluids and ore-forming fluid

[J]. Earth Science Frontiers, 2001, 8(4): 245-251.

[本文引用: 1]

肖荣阁, 张宗恒, 陈卉泉, 等 .

地质流体自然类型与成矿流体类型

[J]. 地学前缘, 2001, 8(4): 245-251.

[本文引用: 1]

Xie Yuling , Tian Shihong , Hou Zengqian , et al .

Discussion of migration and precipitation mechanics in Muluo REE deposit Miannong country, west Sichuan Province: Evidence from fluid inclusion in bastnaeite

[J]. Acta Petrologica Sinica, 2008, 24(3):555-561.

[本文引用: 1]

谢玉玲, 田世洪, 侯增谦, 等 .

四川冕宁木落稀土矿床稀土元素迁移与沉淀机制: 来自稀土矿物中流体包裹体的证据

[J]. 2008, 24(3):555-561.

[本文引用: 1]

Li Yongqiang .

The Coexistence and Symbiosis Relation Research of Jinding Large-Scale Lead Zinc and the Sulfate Ore Deposit

[D]. Xi'an:Changan University, 2006.

[本文引用: 1]

李永强 .

兰坪金顶超大型铅锌矿床与硫酸盐矿床共存共生关系研究

[D]. 西安：长安大学, 2006.

[本文引用: 1]

Xu Jinhong , Zhang Zhengwei , Yang Xiaoyong , et al .

The low-temperature mineralization of structurally-controlled fluids in Dahegou antimony ore deposit, Henan Province

[J]. Acta Geologica Sinica, 2017, 91(12): 2 739-2 756.

[本文引用: 1]

徐进鸿, 张正伟, 杨晓勇, 等 .

河南省大河沟锑矿床构造—流体与低温成矿

[J]. 地质学报, 2017, 91(12): 2 739-2 756.

[本文引用: 1]

Lu Huanzhang , Fan Hongrui , Ni Pei , et al .

Fluind inclusion

[M]. Beijing:Science Press, 2004.

[本文引用: 1]

卢焕章, 范宏瑞, 倪培, 等 .

流体包裹体

[M]. 北京：科学出版社, 2004.

[本文引用: 1]

Frezzotti M L , Tecce F , Casagli A .

Raman spectroscopy for fluid inclusion analysis

[J]. Journal of Geochemical Exploration, 2012, 112(1): 1-20.

[本文引用: 1]

Li Xiaochun , Fan Hongrui , Hu Fangfang , et al .

An analysis of the invidual fluid inclusion by LA-ICP-MS and its application to ore deposit

[J]. Mineral Deposit, 2010, 29(6): 1 017- 1 028.

[本文引用: 1]

李晓春, 范宏瑞, 胡芳芳, 等 .

单个流体包裹体LA-ICP-MS成分分析及在矿床学中的应用

[J]. 矿床地质, 2010, 29(6): 1 017-1 028.

[本文引用: 1]

Sun He , Xiao Yilin .

Fluid inclusion: Latest development, geological application and prospect

[J]. Advances in Earth Science, 2009, 24(10): 1 105-1 121.

[本文引用: 1]

孙贺, 肖益林 .

流体包裹体研究：进展、地质应用及展望

[J]. 地球科学进展, 2009, 24(10): 1 105-1 121.

[本文引用: 1]

Yao Ying , Sun Qiang .

Raman quantitative measurements for carbon isotopic composition in CO2-rich fluid inclusion: A preliminary study

[J]. Advances in Earth Science, 2016, 31(10): 1 032-1 040.

[本文引用: 1]

药瑛, 孙樯 .

应用于流体包裹体CO2碳同位素组成的拉曼光谱定量研究探讨

[J]. 地球科学进展, 2016, 31(10): 1 032-1 040.

[本文引用: 1]

Wei Qing , Fan Hongrui , Lan Tingguang , et al .

Genesis of Sizhuang gold deposit, Jiaodong peninsula: Evidences from fluid inclusion and quartz solubility modeling

[J]. Acta Petrologica Sinica, 2015, 31(4):1 049-1 062.

[本文引用: 1]

卫清, 范宏瑞, 蓝廷广, 等 .

胶东寺庄金矿床成因: 流体包裹体与石英溶解度证据

[J]. 岩石学报, 2015, 31(4): 1 049-1 062.

[本文引用: 1]

Chi Guoxiang , Lai Jianqing .

Roles of fluid inclusion in study of mineral deposit

[J]. Mineral Deposit, 2009, 28(6): 850-855.

[本文引用: 1]

池国祥, 赖健清 .

流体包裹体在矿床研究中的作用

[J]. 矿床地质, 2009, 28(6): 850-855.

[本文引用: 1]

Xu Wengang , Fan Hongrui .

Ore-forming fluids of the oxidized and reduced porphyry deposits

[J]. Earth Science Frontiers, 2011, 18(5): 103-120.

[本文引用: 1]

徐文刚, 范宏瑞 .

氧化性和还原性斑岩型矿床流体成矿特征分析

[J]. 地学前缘, 2011, 18(5): 103-120.

[本文引用: 1]

Xie Yuling , Hou Zengqian , Yin Shuping , et al .

Continuous carbonatitic melt-fluid evolution of a REE mineralization system: Evidence from inclusions in the Maoniuping REE deposit, Western Sichuan, China

[J]. Ore Geology Reviews, 2009, 36(1): 90-105.

[本文引用: 1]

Linke W F .

Solubilities of Inorganic and Metalorganic Compounds (4th ed)

[M]. Washington:American Chemical Society, 1965.

[本文引用: 1]

Eysseltová J , Bouaziz R .

IUPAC-NIST solubility data series. 93. Potassium sulfate in water

[J]. Journal of Physical and Chemical Reference Data, 2012, 41(1): 0131031. DOI: 10.1002/chin.201340220.

[本文引用: 2]

Schroeder W C , Gabriel A , Partridge E P .

Solubility equilibria of sodium sulfate at temperatures of 150 to 350 °C. I. Effect of sodium hydroxide and sodium chloride

[J]. Journal of the American Chemical Society, 1935, 57(9): 1 539-1 546.

[本文引用: 2]

Ding X , Zhang T , Zhang S , et al .

Experimental determination and modelling of the solubilities of sodium sulfate and potassium sulfate in sub-and supercritical water

[J]. Fluid Phase Equilibria, 2019, 483: 31-51.

[本文引用: 1]

Dipippo M M , Sako K , Tester J W .

Ternary phase equilibria for the sodium chloride-sodium sulfate-water system at 200 and 250 bar up to 400 °C

[J]. Fluid Phase Equilibria, 1999, 157(2): 229-255.

[本文引用: 1]

Leusbrock I , Metz S J , Rexwinkel G , et al .

Quantitative approaches for the description of solubilities of inorganic compounds in near-critical and supercritical water

[J]. The Journal of Supercritical Fluids, 2008, 47(2): 117-127.

[本文引用: 1]

Mao S , Peng Q , Wang M , et al .

The PVTx properties of aqueous electrolyte solutions containing Li+, Na+, K+, Mg2+, Ca2+, Cl− and SO 4 2 - under conditions of CO2 capture and sequestration

[J]. Applied Geochemistry, 2017, 86: 105-120.

[本文引用: 2]

Duan Zhenhao .

State equation of geological fluid

[J]. Science in China(Series D), 2010, 40(4): 393-413.

[本文引用: 1]

段振豪 .

地质流体状态方程

[J]. 中国科学: D辑, 2010, 40(4): 393-413.

[本文引用: 1]

Zhong R , Brugger J , Tomkins A G , et al .

Fate of gold and base metals during metamorphic devolatilization of a pelite

[J]. Geochimica et Cosmochimica Acta, 2015, 171: 338-352.

[本文引用: 1]

Pan Aoran , Shan Huimei , Peng Sanxi , et al .

Thermodynamic modeling of thioarsenic species distribution in high As groundwater in Hetao Plain

[J]. Advances in Earth Science, 2018, 33(11): 1 169-1 180.

[本文引用: 1]

潘敖然, 单慧媚, 彭三曦, 等 .

基于热力学模拟河套平原高砷地下水中硫代砷形态分布特征

[J]. 地球科学进展, 2018, 33(11): 1 169-1 180.

[本文引用: 1]

Hu Q C , Guo H R , Lu X B , et al .

Determination of P-V-T-x properties of the CO2-H2O system up to 573.15 K and 120 MPa-experiments and model

[J]. Chemical Geology, 2016, 424: 60-72.

[本文引用: 1]

Mao S , Duan Z .

The P, V, T,x properties of binary aqueous chloride solutions up to T = 573 K and 100 MPa

[J]. The Journal of Chemical Thermodynamics, 2008, 40(7): 1 046-1 063.

[本文引用: 2]

Greenberg J P , Møller N .

The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-K-Ca-Cl-SO4-H2O system to high concentration from 0 to 250 °C

[J]. Geochimica et Cosmochimica Acta, 1989, 53(10): 2 503-2 518.

[本文引用: 3]

Pabalan R T , Pitzer K S .

Thermodynamics of concentrated electrolyte mixtures and the prediction of mineral solubilities to high temperatures for mixtures in the system Na-K-Mg-Cl-SO4-OH-H2O

[J]. Geochimica et Cosmochimica Acta, 1987, 51(9): 2 429-2 443.

[本文引用: 2]

Pitzer K S .

Thermodynamics of electrolytes. I. Theoretical basis and general equations

[J]. The Journal of Physical Chemistry, 1973, 77(2): 268-277.

[本文引用: 1]

Wang L , Zhang W , Yang B , et al .

Solubility measurements in Na-F-CO3-HCO3-H2O system at (308.15 and 323.15) K and development of a Pitzer-based equilibrium model for the Na-F-Cl-SO4-CO3-HCO3-H2O system

[J]. The Journal of Chemical Thermodynamics, 2019, 131: 88-96.

[本文引用: 1]

Parkhurst D L , Appelo C A J .

Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation

Batch-Reaction, Transport One-Dimensional , and

Inverse Geochemical Calculations

[R]. U.S. Geological Survey, 2013.

[本文引用: 1]

Kulik D A , Wagner T , Dmytrieva S V , et al .

GEM-Selektor geochemical modeling package: Revised algorithm and GEMS3K numerical kernel for coupled simulation codes

[J]. Computational Geosciences, 2013, 17(1): 1-24.

[本文引用: 1]

Dai Z , Kan A , Zhang F , et al .

A thermodynamic model for the solubility prediction of barite, calcite, gypsum, and anhydrite, and the association constant sstimation of CaSO4 (0) ion pair up to 250 °C and 22000 psi

[J]. Journal of Chemical and Engineering Data, 2015, 60(3): 766-774.

[本文引用: 1]

Shi W , Kan A , Fan C , et al .

Solubility of barite up to 250 °C and 1500 bar in up to 6 m NaCl solution

[J]. Industrial and Engineering Chemistry Research, 2012, 51(7): 3 119-3 128.

[本文引用: 1]

Dai Z , Kan A , Shi W , et al .

Calcite and barite solubility measurements in mixed electrolyte solutions and development of a comprehensive model for water-mineral-gas equilibrium of the Na-K-Mg-Ca-Ba-Sr-Cl-SO4-CO3-HCO3-CO2(aq)-H2O System up to 250 °C and 1500 bar

[J]. Industrial and Engineering Chemistry Research, 2017, 56 (23): 6 548-6 561.

[本文引用: 1]

Millero F J .

The effect of pressure on the solubility of minerals in water and seawater

[J]. Geochimica et Cosmochimica Acta, 1982, 46(1): 11-22.

[本文引用: 1]

Appelo C A J , Parkhurst D L , Post V E A .

Equations for calculating hydrogeochemical reactions of minerals and gases such as CO2 at high pressures and temperatures

[J]. Geochimica et Cosmochimica Acta, 2014, 125: 49-67.

[本文引用: 2]

Monnin C .

A thermodynamic model for the solubility of barite and celestite in electrolyte solutions and seawater to 200 °C and to 1 kbar

[J]. Chemical Geology, 1999, 153(1/4): 187-209.

[本文引用: 2]

Robie R A , Hemmingway B , Fisher J R .

Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 bar (10⁵ pascals) Pressure and at Higher Temperature

[R]. Denver,CO: U.S. Geological Survey, 1978.

[本文引用: 1]

Rogers P S Z , Pitzer K S .

Volumetric properties of aqueous sodium vhloride solutions

[J]. Journal of Physical and Chemical Reference Data, 1982, 11(1): 15-81.

[本文引用: 1]

Pitzer K S , Peiper J C , Busey R H .

Thermodynamic properties of aqueous sodium chloride solutions

[J]. Journal of Physical and Chemical Reference Data, 1984, 13(1): 1-102.

[本文引用: 4]

Königsberger E , Eriksson G , May P M , et al .

Comprehensive model of synthetic Bayer liquors. Part 1. Overview

[J]. Industrial and Engineering Chemistry Research, 2005, 44(15):5 805-5 814.

[本文引用: 1]

Wagner W , Kruse A , Kurtzschmar H J .

Properties of Water and steam: The Industrial Standard IAPWS-IF97 for the Thermodynamic Properties and Supplementary Equations for Other Properties: Tables Based on These Equations

[M]. Berlin:Springer-Verlag Berlin, 1998.

[本文引用: 1]

Pabalan R T , Pitzer K S .

Thermodynamics of NaOH(aq) in hydrothermal solutions

[J]. Geochimica et Cosmochimica Acta, 1987, 51(4): 829-837.

[本文引用: 1]

Bradley D J , Pitzer K S .

Thermodynamics of electrolytes. 12. Dielectric properties of water and Debye-Hückel parameters to 350 °C and 1 kbar

[J]. Journal of Physical Chemistry, 1979, 83(12): 1 599-1 603.

[本文引用: 1]

Archer D G .

Thermodynamic properties of the KCl+H2O system

[J]. Journal of Physical and Chemical Reference Data, 1999, 28(1): 1-17.

[本文引用: 1]

Rowland D , May P M .

A Pitzer-based characterization of aqueous magnesium chloride, calcium chloride and potassium iodide solution densities to high temperature and pressure

[J]. Fluid Phase Equilibria, 2013, 338: 54-62.

[本文引用: 1]

Møller N .

The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-Ca-Cl-SO4-H2O system, to high temperature and concentration

[J]. Geochimica et Cosmochimica Acta, 1988, 52(4): 821-837.

[本文引用: 1]

Obšil M , Majer V , Hefter G T , et al .

Densities and apparent molar volumes of Na2SO4(aq) and K2SO4(aq) at temperatures from 298 K to 573 K and at pressures up to 30 MPa

[J]. Journal of Chemical and Engineering Data, 1997, 42(1): 137-142.

[本文引用: 3]

Al Ghafri S Z , Maitland G C , Trusler J P M .

Densities of SrCl2(aq), Na2SO4(aq), NaHCO3(aq), and two synthetic reservoir brines at temperatures between (298 and 473) K, pressures up to 68.5 MPa, and molalities up to 3 mol·kg-1

[J]. Journal of Chemical and Engineering Data, 2013, 58(2): 402-412.

[本文引用: 1]

Apelblat A , Manzurola E , Orekhova Z .

Thermodynamic properties of aqueous electrolyte solutions. volumetric and compressibility studies in 0.1 mol.kg-1, 0.5 mol·kg-1, and 1.0 mol·kg-1 sodium carbonate and sodium sulfate solutions at temperatures from 278.15 K to 323.15 K

[J]. Journal of Chemical and Engineering Data, 2009, 54(9): 2 550-2 561.

[本文引用: 1]

Saluja P P S , Pitzer K S , Phutela R C .

High-temperature thermodynamic properties of several 1∶1 electrolytes

[J]. Canadian Journal of Chemistry, 1986, 64(7): 1 328-1 335.

[本文引用: 1]

Chen C T , Emmet R T , Millero F J .

The apparent molal volumes of aqueous solutions of sodium chloride, potassium chloride, magnesium chloride, sodium sulfate, and magnesium sulfate from 0 to 1000 bars at 0, 25, and 50 °C

[J]. Journal of Chemical and Engineering Data, 1977, 22(2): 201-207.

[本文引用: 1]

Ellis A J .

Partial molal volumes in high-temperature water. Part III. halide and oxyanion salts

[J]. Journal of the Chemical Society A: Inorganic, Physical, Theoretical, 1968. DOI:10.1039/j19680001138.

[本文引用: 3]

Saluja P P S , Lemire R J , Leblanc J C .

High-temperature thermodynamics of aqueous alkali-metal salts

[J]. The Journal of Chemical Thermodynamics, 1992, 24(2): 181-203.

[本文引用: 3]

Zezin D , Driesner T , Sanchez-Valle C .

Volumetric properties of Na2SO4-H2O and Na2SO4-NaCl-H2O solutions to 523.15 K, 70 MPa

[J]. Journal of Chemical and Engineering Data, 2015, 60(4): 1 181-1 192.

[本文引用: 1]

Azizov N D , Akhundov T S .

The bulk properties of the Na2SO4-H2O system in a wide range of the parameters of state

[J]. High Temperature, 2000, 38(2): 203-209.

[本文引用: 1]

Laliberté M .

A model for calculating the heat capacity of aqueous solutions, with updated density and viscosity Data

[J]. Journal of Chemical and Engineering Data, 2009, 54(6): 1 725-1 760.

[本文引用: 2]

Azizov N D .

The density and partial properties of K2SO4-H2O solutions from room temperature to 573 K

[J]. Zhurnal Neorganicheskoi Khimii, 1998, 43(2): 323-327.

[本文引用: 2]

Pearce J N , Eckstrom H C .

Vapor pressures and partial molal volumes of aqueous solutions of the alkali sulfates at 25°

[J]. Journal of the American Chemical Society, 1937, 59(12): 2 689-2 691.

[本文引用: 1]

Voisin T , Erriguible A , Philippot G , et al .

Investigation of the precipitation of Na2SO4 in supercritical water

[J]. Chemical Engineering Science, 2017, 174: 268-276.

[本文引用: 3]

/

〈 〉

地址：甘肃省兰州市天水中路8号
QQ：114723517
电话：0931-8762293　E-mail：adearth@lzb.ac.cn
陇ICP备2021001824号-5　 甘公网安备62010202000687