1 引 言
由于重力固体潮信号包括日波、半日波和年波、月波谐波分量,日波和半日波分量能量相对强,年波和月波分量能量相对较弱[1],所以年波、月波信号很容易被湮没。为了更好地对重力固体潮信号进行分析,必须对重力固体潮信号进行分解,将强弱信号进行分离。本文依据重力固体潮信号的产生机理,采用一种重力固体潮三维正交分解模型,应用独立成分分析(Independent Component Analysis,ICA)对信号进行加性分解,再对正交的独立成分分量进行基于互相关的谱分析,凸显弱的潮汐谐波分量,并分析潮汐谐波间的乘性调制关系。
利用ICA分解出多路信号,有利于后续对分解后的独立分量做基于互相关的谱相关分析,避免一路信号只能做自相关,强信号屏蔽弱信号的问题。
在对独立成分分量的谱相关分析中,自相关运算会使强的分量更强,弱的分量更弱,针对这一问题,本文采用独立成分间的互相关谱,实现更高分辨率的谱相关分析,来揭示重力固体潮,谐波分量的调制关系。
2 重力固体潮正交分解模型
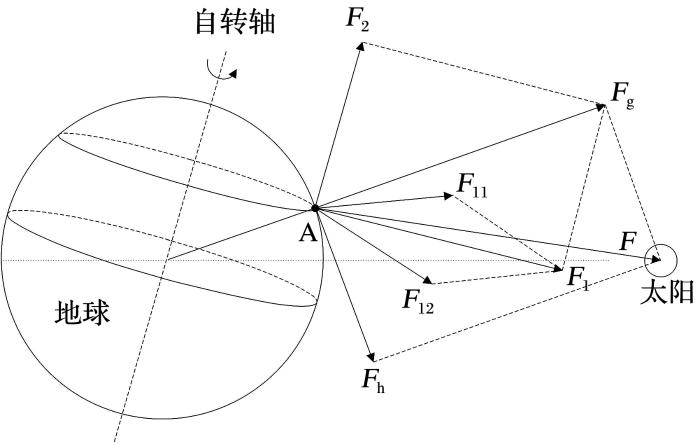
根据重力固体潮信号的产生机理,本文以地球受到的太阳的引潮力为例进行分析,地球受到的月球的引潮力与此类似。当地球围绕太阳旋转时,两者之间的距离会发生改变,反映了地球受到的太阳的引力,即太阳的引力潮[1]。本文的重力固体潮信号分解模型如图1所示。在地球观测点A处受到的太阳的潮汐力,可以被正交分解为重力固体潮信号
图1
图1
重力固体潮正交分解模型
Fig. 1
The orthogonal decomposition model of Gravity Earth Tide signal
3 基于一种新型智能优化算法的ICA
由于地球、月球和太阳共同形成的重力固体潮信号,本文采用ICA对混合信号进行分解。
图2中,
去均值和白化利用的是经典的特征值算法。求解解混矩阵
图2
4 基于互相关的谱相关分析
设
式中:
若
式中:
式中:
式中:
式中:
5 基于ICA的引潮力互相关谱分析
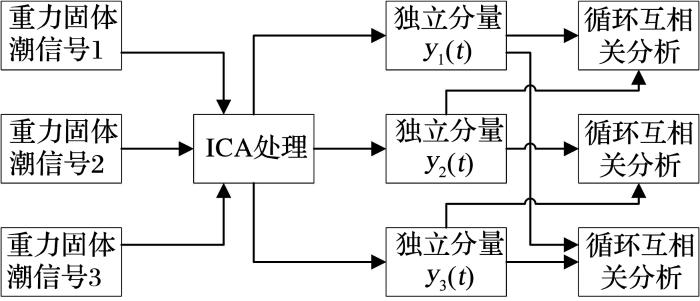
本方法主要是ICA算法与互相关谱分析,包括4个步骤,流程图如图3所示。
(1)获取观测点处的重力固体潮信号。为了便于计算,本文选取同一经度、不同纬度的3路重力固体潮信号。
(2)
(3)对解混输出信号
(4)读取重力固体潮信号中相应的物理信息,并结合潮汐谐波理论计算值[17]进行对比分析(详见下文),进而求出各谐波分量间的调制关系。
图3
图3
ICA与互相关谱分析流程图
Fig. 3
Flow chart of ICA and cross-correlation spectral analysis
6 实验结果分析
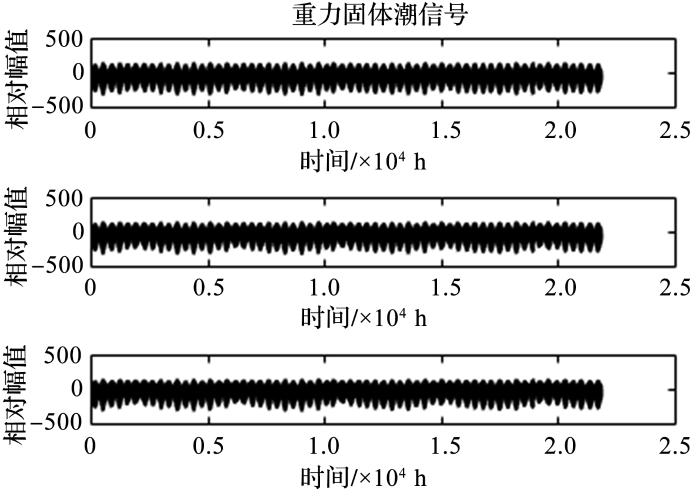
在采样频率为每小时一个样本点,采样长度为2年半的情况下,测得昆明地区的重力固体潮信号如图4所示。
图4
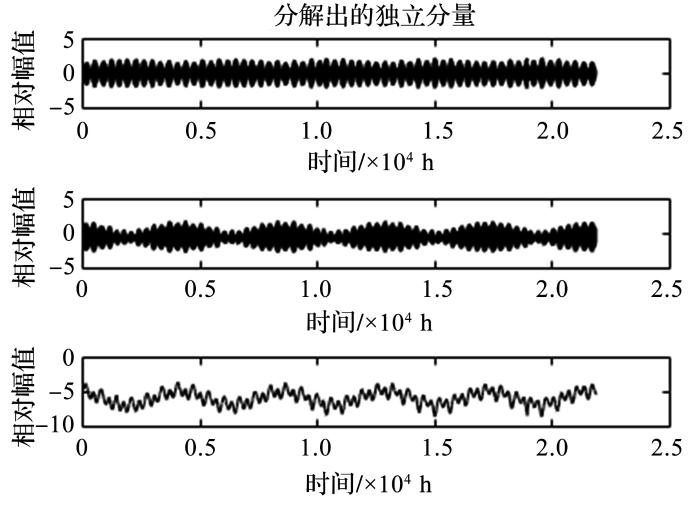
通过本文的基于单形邻域与多角色进化策略的智能优化算法得到的独立分量为
由图5可知,通过ICA算法可以将重力固体潮信号分解成3路独立分量信号,对其频谱进行分析,可知
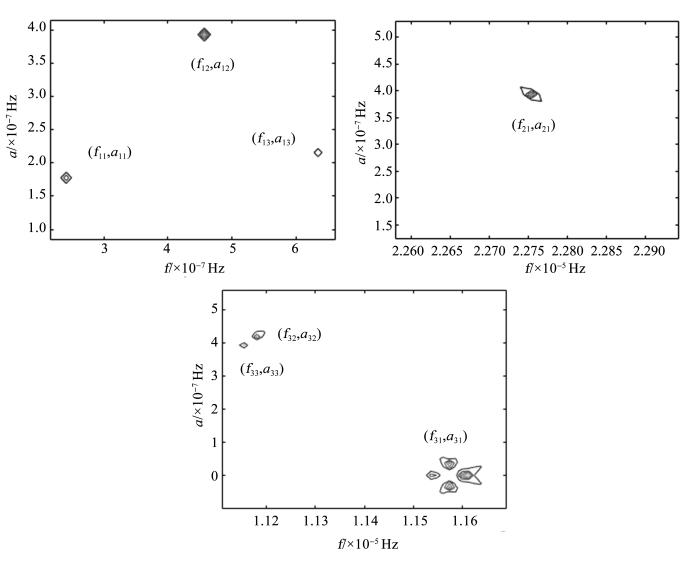
图5
图6
图6
y1(t) ,y2(t)和y3(t)的自相关谱
Fig.6
Autocorrelation spectrum of y1(t),y2(t) and y3(t)
表1 y1(t) ,y2(t)和y3(t)的自相关谱分析
Table 1
| 乘性调制频率/Hz | 解调对应的潮汐谐波频率/Hz | 潮汐谐波频率理论计算值/Hz |
|---|---|---|
图7
图7
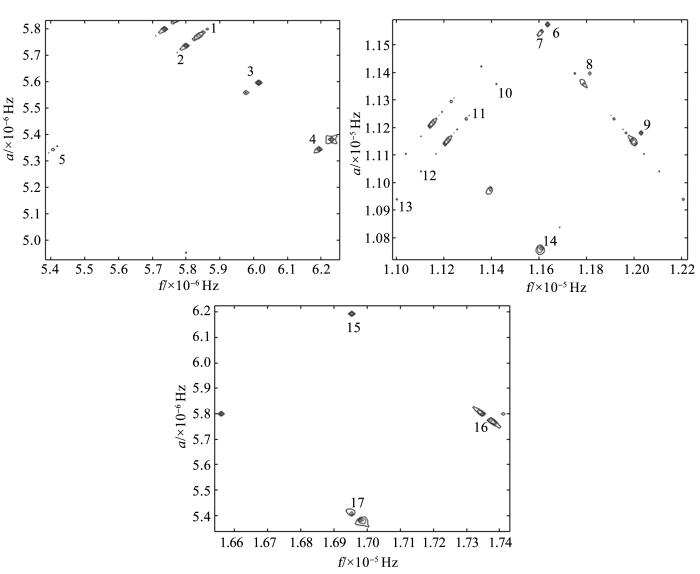
y1(t),y2(t)和y3(t)的互相关谱
Fig.7
Cross-correlation spectrum of y1(t),y2(t) and y3(t)
表2 y1(t),y2(t)和y3(t)的互相关谱峰点
Table 2
| 互相关谱峰点 | ||
|---|---|---|
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | |
表3 y1(t),y2(t)和y3(t)的互相关谱分析
Table 3
| 潮汐谐波理论计算值/Hz | 对应于乘性调制谱相关点 | 对应于线性差频谱相关点 | 对应于线性和频谱相关点 | |
|---|---|---|---|---|
| 长周期波 | ||||
| 1,2,5,6,7,10,11,12,13 | ||||
| 3,8 | ||||
| 4,9,14 | ||||
| 日波 | ||||
| 14 | 15 | 5 | ||
| 9 | ||||
| 8 | 2 | |||
| 7 | 17 | 4 | ||
| 6 | ||||
| 7,14 | 16 | 3 | ||
| 6 | ||||
| 8 | 1 | |||
| 9 | ||||
| 半日波 | ||||
| 13 | ||||
| 12 | ||||
| 14,17 | ||||
| 11 | ||||
| 10 | ||||
| 7,15,16 | ||||
| 6,8,9 | ||||
图8
图8
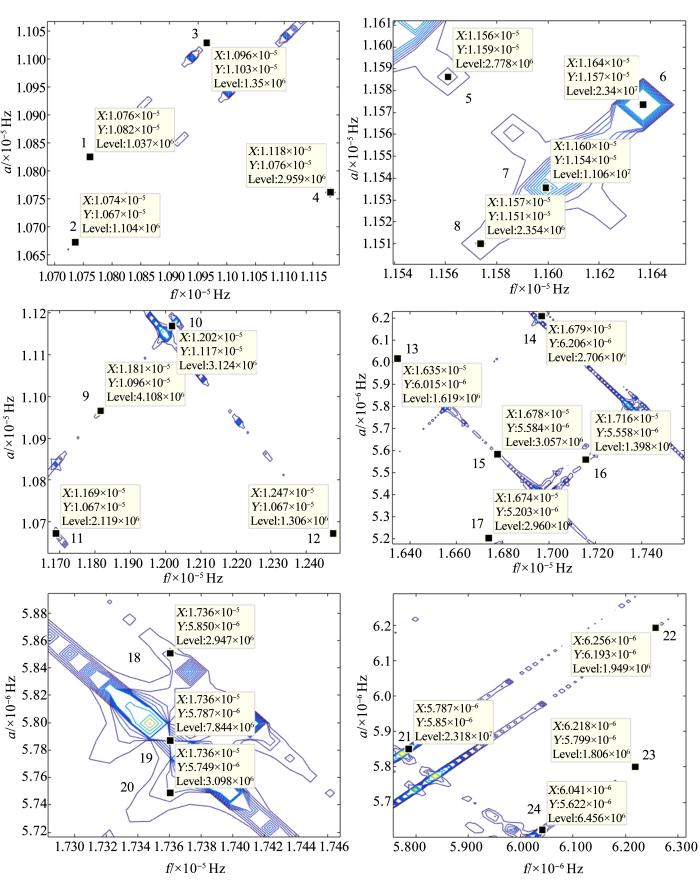
y1(t),y2(t)和y3(t)的部分互相关谱
Fig. 8
Partial cross-correlation spectrum of y1(t),y2(t) and y3(t)
表4 y1(t),y2(t)和y3(t)的部分互相关谱分析
Table 4
| 潮汐谐波理论计算值/Hz | 对应于乘性调制谱相关点 | 对应于线性差频谱相关点 | 对应于线性和频谱相关点 | |
|---|---|---|---|---|
| 长周期波 | 5 | |||
| 1,2,3,21,22 | ||||
| 23,24 | ||||
| 9, | ||||
| 日波 | 13 | |||
| 4,11,12 | 14 | |||
| 4,10 | 15 | |||
| 8 | 18 | |||
| 7 | 17 | |||
| 6,8 | 19 | |||
| 7 | 16,20 | |||
| 6 | 21 | |||
| 11 | 24 | |||
| 10 | 23 | |||
| 12 | 22 | |||
| 半日波 | 2 | |||
| 1 | ||||
| 17 | ||||
| 3 | ||||
| 13,15 | ||||
| 16 | ||||
| 9 | ||||
| 20 | ||||
| 5,19 | ||||
| 14 | ||||
| 18 | ||||
由此可知,通过ICA和互相关谱分析,证明谐波分量间具有明显的直接或间接乘性调制关系。
7 结 论
在实验中,成功将重力固体潮信号分解为3路独立谐波分量:半日波谐波分量、日波谐波分量和长周期波谐波分量,并且分别对应于本文所采用的重力固体潮信号正交分解模型,长周期波分量对应于平行地球自转轴方向的分量,日波和半日波谐波分量对应于平行赤道平面的2个分量,说明各独立信号是通过正交线性叠加形成的重力固体潮信号。
在对分解得到的3路独立成分做互相关谱分析,相对于做自相关运算,可以得到更多的独立谐波分量的谱相关点,大大提高谱相关分析的分辨率。再通过和潮汐谐波频率理论计算值进行比较分析,发现潮汐谐波分量之间普遍存在直接或间接乘性调制的关系,由此证明了本文提出的算法,不但从加性分解的角度有效分离了重力固体潮信号中强度差异比较大的独立成分,而且基于互相关谱,揭示了相应潮汐谐波间乘性调制的关系,揭示出在重力固体潮信号中,潮汐谐波分量之间的叠加与调制方式。
参考文献
Solid Earth Tide
[M].
固体地球潮汐
[M].
Analysis of influence of Earth tide on vertical deformation and gravity change in the Three Gorges area
[J].
固体潮对三峡地区地壳垂直形变和重力变化的影响分析
[J].
Quality assessment of land gravity data in the latest global gravity database V23
[J].
最新全球重力数据库V23中陆域重力资料质量评估
[J].
Spectral correlation analysis of EMD modal components and demodulation analysis of gravity solid tide signals
[J].
EMD模态分量的谱相关分析法及其对重力固体潮信号的解调分析
[J].
Strain and stress tide in Earth
[J].
地球内部应变与应力固体潮
[J].
Seismic precursor information of gravity solid tides extracted by HHT
[J].
基于HHT提取重力固体潮的地震前兆信息
[J].
Identification and extraction of seismic precursor information in tidal deformation data
[J].
潮汐形变资料中地震前兆信息的识别与提取
[J].
The tidal harmonic extraction of gravity solid tide signal based on ICA
[J].
基于ICA的重力固体潮信号的潮汐谐波提取
[J].
Development and application of blind source separation technology
[J].
盲源分离技术的发展及应用浅谈
[J].
Theory and Application of Blind Source Separation
[M].
盲源分离理论与应用
[M].
Independent component analysis using an extended infomax algorithm for mixed sub-Gaussian and super-Gaussian sources
[J].
Blind signal separation
[J].
盲信号分离
[J].
A surface-simplex dwarm rvolution slgorithm
[J].
Non-stationary Signal Analysis and Processing
[M].
非平稳信号分析与处理
[M].
Cyclic and Stationary Signal Processing and Application
[M].
循环平稳信号处理及应用
[M].
Non-stationary Signal Analysis Method Based on Cyclostationary Characteristics
[D].
基于循环平稳特征的非平稳信号分析方法研究
[D].
Gravity and Solid Tide Course
[M].
重力与固体潮教程
[M].
Simulation implementation of global gravity solid tide
[J].
全球重力固体潮的仿真实现
[J].
The calculation of theoretical values of solid tide waves based on laplace series expansion method
[J].
基于拉普拉斯级数展开法的固体潮波类理论值计算
[J].
The calculation of theoretical value of gravity solid tide based on MATLAB
[J].
基于MATLAB的重力固体潮理论值计算
[J].
The computer deduction of the tide level of solid tide
[J].
固体潮引潮位的计算机演绎展开
[J].
The closed formula of the theoretical derivative of gravity tides
[J].
重力固体潮理论值导数的封闭公式
[J].







 甘公网安备62010202000687
甘公网安备62010202000687