作者简介:孙晓敏(1986-),男,内蒙古通辽人,博士研究生,主要从事低渗透介质耦合流的研究.E-mail:sxm.0213@gmail.com
化学渗透现象引起的“耦合流”研究,已广泛应用于地球科学、环境科学和土木工程等多个领域。回顾了自20世纪50年代以来化学渗透以及黏土半透膜效应的研究进展。分别从理论基础、试验研究和数值模型等3个方面综述了黏土岩土的化学渗透效应的理论及其研究进展,重点阐述了化学渗透现象及其黏土半透膜效应的室内试验、场地试验及野外证据以及化学渗透“耦合流”的不连续模型和连续模型。指出今后应重点研究黏性土化学渗透效应对地下水流及溶质运移的影响研究。这将有利于我国进一步开展考虑化学渗透效应的地下水数值模拟研究。
First author:Sun Xiaomin (1986-), male, Tongliao City, Inner Mongolia, Ph.D student. Research areas include coupled flow phenomenon in clayey sediment.E-mail:sxm.0213@gmail.com
*Corresponding author:Wu Jianfeng (1971-), male, Jiujiang City, Jiangxi Province, Professor. Research areas include numerical simulation of groundwater.E-mail:jfwu@nju.edu.cn
Osmotic phenomena refer to water and solute transport processes that occur when transport of solute molecules or ions is restricted by the porous medium relative to that of water molecules. Chemical osmosis and reverse osmosis/ultrafiltration are osmotic phenomena. The studies of “coupled flow” caused by chemical osmosis have been widely applied in many fields, such as earth science, environmental science and civil engineering. This paper provided a review of the considerable advances in the field of chemical osmosis and clay semipermeable membrane since the 1950s. We summarized the research progress of chemical osmosis in clayey sediments into three aspects: theoretical basis, experimental research and numerical model. In particular, the laboratory equipment and measurement methods of the chemico-osmotic efficiency coefficient σ were described,. The existing discontinuous models based on the ‘diffusive double layer’ theory were summerized, as well as the various control factors of σ. It increases with Cation Exchange Capacity (CEC), compaction pressure and decreases by the increasing of porosity and solution concentration. This paper also summerized the contimuum models based on non-equilibrium thermodynamics, which are used to explain and predict anomalies of hydraulic head pressure and salinity in clayey environments. For the future development of this discipline, it is critical to find a reliable method to confirm the σ value. It is also critical to emphasize the research on chemical osmosis in complex conditions and the influence of chemical osmosis on groundwater flow and solute transpotation. China has just stepped into this research area and more efforts should be made if significant progress is desired. This review will be helpful to further research on groundwater numerical simulation integrated with chemical osmosis in China.
富含黏土矿物的沉积物或页岩由于渗透系数很低, 因此, 在地下水流运动、溶质运移的研究中, 常被认为是不透水或弱透水的。在此基础上建立地下水流及其溶质运移模型时, 对流项是被忽视掉的, 而弥散作用在溶质运移中占主导地位。然而, 研究者发现黏土并不是完全隔水的, 因此在水头梯度下会发生越流现象。一些学者也从不同尺度的试验中得到了黏土的渗透系数、弥散度等参数并成功应用在其提出的对流— 弥散模型中[1]。模型中, 在水头梯度下的水流运动以及在浓度梯度下的溶质运移分别遵循Darcy定律和Fick定律。在20世纪中期, 随着化学渗透现象以及半透膜性质的发现表明:在一些低渗透的黏土介质中, 黏土可以表现出类似于生物半透膜的选择性渗透的性质。在此情况下, 浓度梯度也可产生相应的渗透压力, 发生化学渗透现象以及超滤现象, 这种由不同梯度所驱动水流流动的现象称之为“ 耦合流” 现象[2]。由化学梯度所产生的渗透压力会很大程度的影响地下水流运动甚至会远远超过水头压力而成为影响地下水流动的主要因素。因而, 用传统的Darcy定律来刻画地下水流动往往是欠妥的。
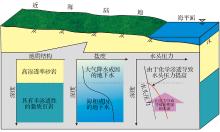
化学渗透现象这种由水头梯度及浓度梯度共同驱动的耦合流的现象最初被用来解释沉积盆地异常的水头压力及其异常的盐度情况[3~6](图1)。近几十年来, 低渗透性的黏土或页岩中的化学渗透在地球物理方面[7~10](如地下水在不饱和多孔介质中的运移; 二氧化碳的地质封存; 沉积盆地的水文地质环境演化过程等)、环境科学[11~14](如污染土壤的修复; 污染物在黏土屏障中的运移和污染物填埋以及核废料储存等)或土木工程[15](如斜坡稳定性的处理; 建筑材料的耐久性研究等)等研究中被考虑进来。另外, 化学渗透现象在石油工业(钻井的稳定性研究)等方面也有所应用[16~18]。因此, 开展黏土的膜性能以及化学渗透等耦合流现象的研究具有重要的理论意义以及实际应用价值。
随着对黏土半透膜性质以及化学渗透现象认识的加深, 越来越多的研究得以开展。在中国, 关于黏土半透膜的化学渗透现象仅有少量研究[19, 20]。根据其研究目的的不同, 研究方法也各有不同, 本文拟从以下3个方面介绍关于黏土半透膜性质及其化学渗透现象的研究现状:①理论基础介绍, 包括化学渗透现象和黏土的半透膜性质; ②试验研究, 依据尺度的区别包括室内试验和场地试验; ③数值模型, 包括不连续模型和连续模型。
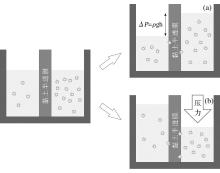
如果2种不同浓度的溶液隔以半透膜时, 水分子或其他溶剂可以从水势高(浓度低)的溶液通过半透膜进入水势低(浓度高)的溶液中, 这种现象称之为“ 渗透现象” (osmosis)。该词语来自于希腊语“ ω σ μ σ ω ” , 意为:“ 推” 。通常来说, 我们所指的渗透现象是指非水头驱动水流的现象。化学渗透(或反渗透、超滤)是由化学梯度(即浓度梯度)为驱动力的一种渗透现象(图2a)。
化学渗透压是由于半透膜两端的化学势能差导致, 渗透压π (kPa)的计算公式如下[21]:
式中:R为热力学常数, 其值为8.314 J/(mol· K); T为热力学温度(K); V为水的摩尔体积(m3/mol);
或:
式中:v是解离常数(对于NaCl来说, v=2); Δ C为半透膜两端的浓度差(mol/L)。以0.1 mol/L的NaCl溶液为例, 在25 ℃下, 由此公式可以计算得出半透膜两端理论的渗透压力差为495.5 kPa, 接近于50 m的水头压力。
反渗透又称作超滤, 是指高浓度一端的溶液受到一个高于渗透压力的水头压力时, 溶剂会逆着自然渗透的方向作反向渗透。由于半透膜的选择性渗透特征, 溶剂分子会被选择性地截留在高浓度端, 从而在半透膜的低压端得到透过的溶剂, 即渗透液; 高压端得到浓缩的溶液, 即浓缩液(图2b)。
与传统的生物半透膜相比, 黏土或黏质页岩的半透膜性质主要归因于黏土颗粒表面的“ 双电层” 性质。在透水性好的含水层中, 多数孔隙水溶液中的离子不会被“ 双电层” 所影响而自由通过。相反的, 在富含黏土物质的沉积物中, 当黏土受到充分的、足够大的压力时, 黏土颗粒的间距减小而使“ 双电层” 重叠, 溶液中的带电粒子由于电荷排斥而难以通过黏土介质。相反的, 水作为不带电的分子, 可以不受排斥而通过。
黏土作为天然的“ 半透膜” , 约束溶质迁移但容许溶剂迁移的能力可以用化学渗透率系数ω [22]或反射率系数σ [2]来表示, 在国内的相关文献中采用了化学渗透效率系数 σ 来表征该能力[19, 20], 本文采用国内相应说法进行论述。
Katchalsky等[23]提出了化学渗透率系数 σ 为半透膜两端达到平衡时的化学渗透导致的水头压力(Δ P)与理想的渗透压的比值:
式中:J为通过半透膜的渗流速度(m/s), Δ P和Δ π 分别为水头压力差与理想渗透压的变化值。
化学渗透率系数 σ 的取值为0~1, 对于无选择通过的介质, σ =0, 此时, 化学渗透作用不存在, 溶液在介质中只存在对流— 弥散现象。对于完全限制溶质通过的黏土介质, σ =1。目前, 只有人工制备的有机高分子半透膜是理想的半透膜。在自然条件下的黏土半透膜都是非理想的半透膜, 化学渗透率系数介于这2种极限之间。
黏土的膜性能及化学渗透(反渗透或超滤)现象最初被用来解释观察到的传统水文地质理论难以解释的异常水头压力或异常的水质浓度等现象。Hanshaw等[5]认为在美国西南部San Juan盆地的白垩层的上部与Paradox盆地的古生代地层组成了一个典型的化学渗透系统(图2a)。Paradox盆地的含水层中的孔隙水由于矿化度较高而使San Juan盆地白垩层中的地下水流入其中, 由于2层相对封闭, 因此异常的水头值可以持续保持。Wood[24]通过分析取自Saginaw构造层位与Glacial含水层中的将近300个水样和60个溪流水样发现, 地下水系统中会发生反渗透现象而影响地下水中的离子分布。
然而, 除了化学渗透现象以外, 引起地下水系统产生异常压力以及盐度情况的原因多种多样, 如何确定其原因是否是由于化学渗透现象以及化学渗透现象可以引起多大的异常压力, 就需要通过试验来确定黏土的膜性能能力的大小, 试验方式依据尺度类型分为室内试验和场地试验。
关于黏土、黏质页岩的化学渗透现象, 研究者们在很多室内试验中(黏土样品厚度在10 mm左右)得到证明, 试验装置大同小异, 类似于渗透仪, 分为刚性壁与柔性壁渗透仪2种。
由于黏土样品处于与其孔隙水浓度不同的试验溶液中会发生膨胀(孔隙水浓度较高时)或收缩(孔隙水浓度较低时), 在硬壁式渗透仪中, 黏土样品的这种性质可能会在膨胀时发生挤压变形或在收缩时使黏土样本与渗透仪边壁分离而产生渗漏。而柔性壁渗透仪边壁可以随土样的变形而变形。另外, 柔性壁渗透仪具有更加方便的改变围压环境以模拟样品的埋藏深度等优点。因此, 近年来, 越来越多的研究者开始采用柔性壁渗透仪来进行渗透试验[6, 25, 26]。
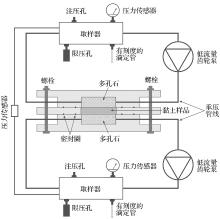
图3为1个典型渗透试验装置[20], 整套装置包括:1个渗透仪用来装配黏土样品; 2个取样器以及相应的测量装置用来改变试验溶液和测量试验结果; 齿轮泵用来循环加入取样器中的试验溶液; 以及连接各个装置的可以承受一定压力的管线、阀门等。另外, 可以根据试验目的增加1套增压装置以进行反渗透(超滤)试验。
在进行化学渗透试验之前, 通常会对黏土样品的渗透系数进行测定, 测定方法为在与黏土样品的两端相连的取样器中加入相同浓度的溶液, 样品两端的浓度差Δ Cs=0, 则由van’ t Hoff关系式可知样品两端的渗透压Δ π =0。在一端的取样器中施加一定的水头压力Δ P, 则渗透系数可以通过Darcy定律计算得出:
式中:Jw为测量得到的水流量(m3/s), K为渗透系数(m/s), A为黏土样品的面积(m2), x为黏土样品的厚度(m)。
渗透系数测定之后, 改变某一端的取样器中的溶液浓度, 土样两端存在一个固定的浓度梯度Δ Cs, 化学渗透率系数σ 通常可以通过以下几种方法测量所得:
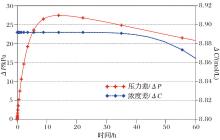
(1) 直接测量黏土样品两端的压力差(图4), 通过公式3计算可以得出σ 。
(2) 将黏土样品两端容器敞开, 黏土样品两端的流量交换量J可以通过安装在容器上的带刻度的滴管测量得出, 则σ 可以通过类似于Darcy定律计算得出:
(3) 通过反渗透(超滤)试验来测量化学渗透率系数, 即通过评估黏土的阻盐能力来评估黏土的膜性能。化学渗透率系数σ 通过以下公式计算而来:
式中:CL与CH分别为淡水端容器与咸水端容器中的溶液浓度(mol/L)。
(4) 通过对土样的力学性质的测量, 如孔隙度n, 阳离子交换容量(Cation Exchange Capacity, CEC), 黏土的比表面积As等, 利用Bresler[27]和Marine等[28]提出的不连续模型, 可以计算出σ 。本文在下一节对主要的不连续模型有专门介绍。
图4为化学渗透试验典型的压力差以及浓度差随时间变化示意图, 黏土两端存在浓度梯度后, 由浓度梯度产生的渗透压力会随着时间的增长而迅速变大。由于黏土所表现出的半透膜性质是不理想的, 不能完全阻隔溶质通过黏土样品, 在试验过程中, 较高浓度的离子由于弥散作用渐渐通过样品进入低浓度的取样器中, 使得样品两端的浓度差逐渐降低, 因此, 压力差达到峰值后, 由浓度差引起的化学压力差会减小。
自1960s以来, 研究者们本着不同的目的, 对不同类型的黏土用以上方法进行了大量的试验, 以观察黏土的半透膜性质。受限于技术原因和经济原因, 相对于室内试验, 关于黏土的膜性能的场地尺度的试验较少。Neuzil[29]在美国中部Dakota页岩中进行的黏土膜性能试验第一次为黏土的膜性能及化学渗透现象提供了最直接的证明。研究者在当地的白垩纪页岩中钻了4个孔, 向其中2个钻孔中加入10倍于页岩孔隙水浓度(35 g/L)的NaCl溶液, 1个钻孔加入去离子水, 1个钻孔加入与页岩孔隙水浓度相当的溶液(复制水)作为参照。在9年时间内监测各孔内的水位变化及水化学成分, 分析结果表明:在高浓度溶液的钻孔中, 化学渗透使页岩中的孔隙水被吸出, 井内的水位在9年时间里较注入复制水的钻孔水位高出约2 m。同时, 加入去离子水的井内也由于化学渗透作用使孔内的矿化度增高。Neuzil[29]通过其提出的计算式计算得出当地页岩的化学渗透率系数分别为0.04(高浓度的咸水)和0.14(去离子水)。
类似的, Noy等[30]在瑞士中部的侏罗纪的Opalinus黏土中进行的场地试验同样提供了化学渗透现象的野外证据。该试验基地属于法国核废料存储基地。试验者们在该地进行了一系列的水文地质调查。化学渗透试验属于其中一部分, 试验者对取自当地的黏土样品进行了化学渗透率效率的实验室测定及其场地试验, 在场地试验中, 试验者将钻孔密封, 通过突然改变钻孔内的液体浓度(去离子水或盐卤水)来观察孔内的水头变化, 结果发现:由于化学渗透作用的存在, 孔内水位会随着液体浓度的变化而变化, 当加入盐水时, 孔内水位会明显升高, 并可以持续很长时间, 可以认为达到了渗透平衡。
近年来, 随着技术的进步, 研究者们陆续对化学渗透现象开展了场地试验[31, 32], 试验目的与方法大同小异, 在此不做赘述。
综上所述, 通过直接测定、间接测定(反渗透)和场地试验等方法进行化学渗透率系数的测定, 试验方法不同、取材不同与评估方法不同所测定化学渗透率系数差异也很大。测得的化学渗透率系数为0.00002~0.99。另外, 也有少量试验所测定的渗透率系数为负。天然黏土的化学渗透率系数的量级大约为0.02[33]。前人一系列的试验研究表明, 黏土的化学渗透率系数与许多因素有关, 包括黏土的应力状态、类型、矿物组成、孔隙水中溶质的种类和浓度等。一般的, 随着黏土中有效应力、黏土的阳离子交换能力的增加而增加; 随着孔隙度的、溶质浓度等的增加而减小(黏土半透膜膜性能能力的详尽性质如表1所示)。
| 表1 化学渗透试验中不同参数对黏土膜性能能力的影响 Table 1 Experimental determined factors affecting the ideality of natural clayey membranes |
第一个考虑低渗透黏土介质中的化学渗透的耦合流模型是20世纪50年代末提出的, 包括不可逆热力学模型、质量传输模型和Mason-Lonsdale模型等[43], 到70年代已趋于成熟。理论模型包括不连续模型和连续模型。
关于化学渗透现象的不连续模型主要是根据黏土半透膜两端的浓度差和压力差来评估膜性能, 这种方法已经被广泛运用于实验室中计算平均膜性能。另外, 一些研究者通过理论分析来确定黏土的孔隙度、黏土颗粒的排列方式、黏土颗粒与孔隙水离子的交互性质(如黏土的阳离子交换能力等)、黏土的排盐作用及双电层厚度、黏土的孔隙水浓度等参数与黏土膜性能之间的关系。以上研究大部分基于Donnan膜平衡理论、Teorell-Meyer-Siever理论和Gouy-Chapman双电层理论, 表2中对各种不连续模型进行了总结。
为确定各模型的适用性, 对取自华北平原的原状土进行的化学渗透试验结果[20]与各不连续模型的计算结果进行了比较, 对比结果可知, 简单模型[33]、KC模型[23]以及FM模型[39]计算出的σ 较化学渗透试验的测量结果高出许多, Bresler模型[27]、均质模型[44]、Bolt模型[45, 46]以及三层模型[47, 48]的计算结果与实验室测定的结果较为相近, 是较为合理的不连续模型。相较于其他模型而言, Bresler模型只需黏土的双电层水膜厚度和试验溶液浓度即可计算出σ , 是一种较为实用且可信的不连续模型。
| 表2 主要的不连续模型概述 Table 2 Summary of the discontinuous models for chemical osmosis |
不连续模型仅能根据半透膜两端稳定时的状态来衡量膜性能能力, 不能很好地解释渗透现象的压力和浓度随时间变化的情况。因此, 建立合理的连续模型可以对压力和浓度的瞬时状态进行模拟。
Greenberg等[49]通过一维模型验证了美国加州的Oxnard盆地的地面沉降是由化学渗透而导致黏土层固结所引起的, 进而引起海水入侵。类似的, 运用该模型模拟了化学渗透引起的黏土半透膜的压缩固结。Noy等[30]改进了该模型对其在瑞士的Opalinus黏土的室内试验以及场地试验结果进行了拟合, 得到了比较好的效果。
Sherwood等[50]假设一个理想的解离系数ν =2的离子溶液, 穿过黏土半透膜的溶液浓度变化可以忽略, 通过Kedem-Katchalsky模型[51, 52]可以得到一个由3个系数(k, D和1-σ )控制的瞬流模型来解释膜性能试验结果, 该模型在简化了化学渗透模型的情况下可以对试验结果进行很好地拟合。但是, 当溶液的离子组分变得复杂时会使未知系数增多, 比如溶液中的离子组分包括1种阳离子和2种阴离子时, 会产生6个未知的系数, 当溶液的离子组分包括2种阳离子与2种阴离子时, 未知系数会增加到13种, 从而使模型失效。有时, 将离子组分近似为单一的阳离子与阴离子可以对化学渗透试验的结果进行粗略模拟。
Malusis等[53]提出了一种复合的迁移模型, 模型中考虑了多种的离子种类以及阴阳离子的交换。在模型中, 研究者使用的测量值以及一些经验系数作为不可逆热力学公式的唯象系数。模拟结果较传统的对流— 弥散模型相比更加符合试验结果。但是模型只考虑化学渗透率系数为零时的情况, 未能反映出化学渗透效率由浓度之间的关系。
Bader等[14], Kooi等[54]和Garavito等[55]提出了一个Spiegler-Kedem模型[26]的一般化模型, 模型中, 液体密度ρ 是由压力与溶液浓度共同决定的, 黏土介质的孔隙度n是由压力决定的:
ρ =ρ 0
n=1-(1-n0)e-α P (8)
式中:ρ 0为纯水的密度(kg/m3); α , β 分别为固体骨架和液体的压缩系数(Pa-1); n0为固体骨架的初始孔隙度。
由不可逆热力学导出的水流Jv(m/s)及溶质流
式中:k为黏土的渗透率(m2), μ 为液体的动力黏度(kg/ms), Ñ C为半透膜两端的浓度差(mol/L)。
由公式(9)和(10)可知, 当σ =0时, 黏土不具有膜性能, 公式(9)即为Darcy方程, 公式(10)简化为传统的对流— 弥散方程; 当σ =1时, Js=0。说明, 当黏土呈现理想的半透膜性质时, 溶质运移会被完全阻止。
对溶液及溶质的质量守恒方程可知:
将公式(9), (10)代入公式(11), (12)可以得到半透膜两端的压力以及浓度随时间变化的一般微分方程。
Bader等[14]利用此模型, 对室内试验结果进行了模拟, 利用试验测得参数值和合理的经验值, 模拟结果跟试验结果得到了很好地拟合。Garavito等[55]利用该模型对Neuzil[29]在美国中部的Dakota的Pierre页岩中关于化学渗透的场地试验结果进行了数值模拟。该模型可以很好地匹配钻孔内的水头压力, 但盐水井内的矿化度较模拟结果更早的达到了最小值, 研究者认为, 由于加入盐水浓度较高而使部分芒硝析出, 从而使井水的矿化度过早达到最小值, 浓度曲线在后期拟合较好。同样, Garavito等[31]也对比利时的地下实验室(Underground Research Laboratory, URL)进行的场地试验进行了数值模拟, 由此可知, 该模型对室内试验以及场地试验均有很好的适用性。此外, 也有研究者利用此模型对试验数据进行了模拟分析[6, 32, 56]。
另外, 一些研究者在考虑化学渗透对地下水流影响的同时也考虑了电渗透、热渗透等驱动力。Soler[12]在研究放射性核素迁移时, 将对流、化学渗透、超滤、化学扩散、热等因素考虑到其一维模型中。Koniorczyk等[57]提出一种复杂的数值模型来模拟水泥灰浆中的盐分在非等温情况下的运移情况。该模型包括5个平衡方程:空气的质量平衡方程, 液体以及蒸汽的质量守恒方程, 溶于水中的液体离子的质量守恒方程, 多相介质的熵平衡和介质的动量守恒方程。作者通过模拟认为, 在建筑物中的材料具有一定的膜性能(σ =0.4), 在处理建筑物稳定等问题时应该将化学渗透现象考虑进去。
一系列的研究工作表明, 化学渗透与反渗透现象对低渗透黏土地下水流动和溶质运移等有显著影响。国外关于化学渗透现象的研究, 无论是室内试验、场地试验以及数值模型上均取得了相当的成果。开展黏土膜性能和化学渗透现象的研究, 对沿海地区的海水入侵、污染物填埋和核废料储存等, 具有非常重要的理论意义和实际的应用价值。根据以上对黏土膜性能和化学渗透现象的研究进展的评述, 以及我国在本学科的研究现状, 对该学科的研究做了以下展望:
(1) 随着对化学渗透现象研究的深入, 出现了多种评估黏土膜性能能力的方法, 包括试验方法和不连续模型等方法, 相同的黏土样品的膜性能能力由于评估方法的不同而呈现出相当大的差异。因此, 需要确定一种比较可信的评估手段, 以精确量化化学渗透对地下水流及溶质运移的影响程度。
(2) 在化学渗透的研究中, 通常只考虑到单种溶质而忽略了黏土介质对不同离子的排斥作用的差异。另外, 在一些特殊的情况下, 渗透现象可以由其他驱动势能导致, 如电渗或热渗, 在处理诸如核废料存储等问题时, 可以将此类渗透现象考虑进来。在今后的研究中, 应该增加对复杂条件下的化学渗透现象的研究。
(3) 在以往的连续模型中, 在确定了黏土膜性能能力之后, σ 通常被认为是一个常量。而实际上, σ 是一个随着化学渗透过程的进行而不断变化的变量。同时, 目前关于地下水的研究中还仍未将化学渗透现象考虑在传统的地下水数值模型之中, 在今后的研究中, 可以考虑将化学渗透现象与传统的地下水数值模型相耦合以对比当存在化学渗透现象时的模拟结果(流场以及浓度分布)的不同。
(4) 与国外相对成熟的研究成果相比, 国内研究相对较少, 目前, 仅见有少量的室内试验方面的研究, 场地试验等方面的研究仍处于空白阶段。我国幅员辽阔, 存在很多类似的天然的化学渗透系统, 如华北平原典型咸淡水区域, 近海区域等, 在今后的研究中, 应将黏性土化学渗透效应对地下水流及溶质运移的影响考虑进来。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|