EMD模态分量的谱相关分析法及其对重力固体潮信号的解调分析

引用本文

全海燕, 刘艳. EMD模态分量的谱相关分析法及其对重力固体潮信号的解调分析. 地球科学进展, 2016, 31(9): 919-925
Quan Haiyan, Liu Yan. The Cyclic Spectrum Analysis of IMFs of EMD and Its Application to Gravity Tide. Advances in Earth Science, 2016, 31(9): 919-925 复制到剪切板

Doi:10.11867/j.issn.1001-8166.2016.09.0919
Permissions

EMD模态分量的谱相关分析法及其对重力固体潮信号的解调分析

全海燕, 刘艳^*

昆明理工大学信息工程与自动化学院, 云南昆明 650500

*通信作者:刘艳(1988-),女,安徽宿州人,硕士研究生,主要从事信号处理研究.E-mail:liuyan8785@163.com

作者简介:全海燕(1970-),男,云南石屏人,副教授,主要从事信号处理、智能优化研究.E-mail:quanhaiyan@163.com

基金:国家自然科学基金项目“提取重力固体潮信号中地球物理信息和地震前兆信息的关键信号处理算法研究”(编号:41364002)资助

摘要

EMD方法分解得到的模态信号分量一般为调频调幅波。提出利用循环相关谱对EMD分解的模态分量进行解调,以分解出模态分量中的载波成分和被调制成分,从而实现对信号的加性分解和乘性解调,揭示信号中各成分分量的物理意义。在应用实验中,将该方法用于重力固体潮信号分析,完整提取出半日波分量、日波分量和半月波分量,并揭示出:在重力固体潮信号中,日波和半日波是加性叠加关系,半月波以乘性调制方式被同时调制到半日波分量和日波分量中,而且,它们之间的调制方式为抑制载波调制方式。

关键词: EMD; 循环谱; 解调; 重力固体潮

中图分类号:P312.4 文献标志码:A 文章编号:1001-8166(2016)09-0919-07

The Cyclic Spectrum Analysis of IMFs of EMD and Its Application to Gravity Tide

Quan Haiyan, Liu Yan

Kunming University of Science and Technology, Faculty of Information Engineering and Automation, Kunming 650500,China

Corresponding author:Liu Yan(1988-), female, Suzhou City, Anhui Province, Master student. Research areas include signal processing.E-mail:liuyan8785@163.com

First author:Quan Haiyan(1970-), male, Shiping County, Yunnan Province, Associate Professor. Research areas include signal processing, intelligent optimization algorithm.E-mail:quanhaiyan@163.com

Fund:Project supported by the National Natural Science Foundation of China“Research of algorithms of extracting both the geophysical information and the seismic precursory information from Gavity Tide” (No.41364002)

Abstract

IMFs sifted out by EMD are the FM-AM components. In the paper, by the cyclic spectrum analysis, IMFs are demodulated as the two periodic components which are identical to the intrinsic physical concepts. Using the method, the half-day-tide M₂, the day-tide O₁, and the half-month-tide M_f are extracted from the gravity tide signal, and a conclusion is drawn that the half-day-tide M₂ and the day-tide O₁ are primary components of gravity tide signal, and the half-month-tide M_f is modulated in the half-day-tide M₂ and the day-tide O₁.

Keyword: EMD; Cyclic spectrum; Demodulation; Gravity tide.

Show Figures

1 引言

在太阳、月亮等天体的潮汐引力作用下, 地球会产生沾弹性形变现象, 反映这种现象的可观测地球物理信号是重力固体潮信号^[1]。这种重力潮汐的变化可以影响地壳应力的变化, 积累大量的能量在地壳岩层中, 以致触发地震^[2]。同时, 重力固体潮信号反映了太阳、月亮等天体潮汐引力的周期变化, 若能从重力固体潮信号中单独分离出各个天体的潮汐引力分量, 揭示各分量间的叠加关系, 将能更深刻的理解天体间重力作用规律^[3]。所以, 重力固体潮信号的分析是地球物理与地震研究的重要方面。从重力固体潮信号的产生机理可以看出, 它是一个多周期的合成信号^[4]。为了反映这些分量之间的关系, 文献^[4]中, 引入EMD(empirical mode decomposition:经验模式分解)方法分析重力固体潮信号, 得到了日波与半日波分量。但由于EMD分解所得的模态分量一般为调频调幅波^[5~9], 所以, EMD分解所得的模态分量并未揭示重力固体潮信号中的乘性调制关系。在循环平稳分析理论中^[10~15], 循环相关谱描述了信号频谱间的乘性调制关系, 据此, 本文提出如下的信号分解方案:首先用EMD对信号进行加性分解, 然后通过循环相关谱分析EMD模态分量的乘性调制关系, 从而清晰揭示信号中各分量间的关系。用该方案对重力固体潮信号进行分析, 结果成功解调出半日波分量、日波分量和半月波分量, 并揭示出:半日波和日波分量间的谱关系是加性叠加关系。半月波分量与半日波分量、半月波与日波分量间均是乘性调制关系, 从而完整给出了重力固体潮信号中, 各分量间的谱关系。

2 EMD方法

通过Hilbert变换可以求取单基频信号的瞬时频率和瞬时幅值。为了实现信号高分辨率的时频分析, Nordeng等引入EMD筛选方法^[5~9]。利用该方法, 可将信号分解为一系列瞬时单基频的模态分量。再通过Hilbert变换, 即可求得这些模态分量的瞬时时频分布和时能分布, 从而实现对信号的时频分析。EMD筛选方法的步骤如下:

(1) 对要分析的信号s(t), 首先找出其全部极值点, 然后将其所有极大值点用3次样条插值法构造出上包络, 同样将其所有极小值点用3次样条插值法构造出下包络, 并求出这2条包络线的平均值m(t)。之后用s(t)减去m(t)得到第一次筛选出的分量h(t), 即:

$\begin{matrix} h (t) = s (t) - m (t) \end{matrix}$ (1)

(2) 将h(t)作为新的s(t), 重复步骤(1), 直到h(t)满足下面的模态信号定义条件:

a:h(t)曲线的上下2条包络线关于时间轴局部对称。若h(t)的上下包络线分别为a1(t)和a2(t), 则对任意的t, 有:a1(t)+a2(t)=0。

b:h(t)曲线的零点和极点交替出现, 即零点数和极点数相等或至多相差1。所得h(t)即为一个模态分量, 记为c₁(t)。

(3) 得到第一个经验模态分量(Intrinsic Mode Function, IMF)后, 可进一步求取残余函数r₁(t)为:

$\begin{matrix} r_{1} (t) = s (t) - c_{1} (t) \end{matrix}$ (2)

将残余函数r₁(t)视为新的s(t), 据此重复步骤(1)和(2), 依次得到第二个模态分量c₂(t), 第三个模态分量c₃(t), ……。直到残余函数r_n(t)为单调函数或足够小为止。

通过上面的3步, 可得到s(t)的分解式为:

$\begin{matrix} s (t) = \overset{n}{\sum_{i = 1}} c_{i} (t) + r (t) \end{matrix}$ (3)

式中:s(t)为分解信号; c_i(t)为EMD分解得到各个模态分量; r(t)为最终残余函数, 表示信号的趋势项, 应单调。

根据步骤(2)中模态分量的定义, EMD方法分解得到的模态分量一般为调频调幅波, 显然, 其载波和被调制波为乘性关系。在实际应用中, 将调频调幅波解相关为载波分量和被调制分量, 对其进行独立分析, 更能得到与实际物理意义相一致的结果。在本文中, 利用谱相关对EMD分解得到的模态分量进行循环平稳分析, 实现对模态分量的解调。

3 二阶循环平稳理论与谱相关

对于随机信号, 可根据其统计量是否随时间变化, 分为平稳随机信号和非平稳随机信号。平稳随机信号由于其统计量的平稳特性, 已建立了完善的分析方法。非平稳随机信号的统计量是随时间变化的, 所以, 对该类信号的分析变得复杂许多。有一类特殊的非平稳信号, 其统计特性随时间周期性的变化, 即其统计特性是周期平稳的, 称其为循环平稳信号, 为了分析这类信号, 建立了循环平稳理论^[10~15]。

设{x(t)}为一循环平稳信号, 根据时间遍历特性, 可以定义信号的二阶循环统计特性— — 循环自相关函数:

$\begin{matrix} \begin{matrix} R_{x} (t, τ) = \lim_{x \to \infty} \frac{1}{2 N + 1} \overset{N}{\sum_{n = - N}} x (t + τ / 2 + n T_{0}) \\ \times x^{*} (t - \frac{τ}{2} + n T_{0}) \end{matrix} \end{matrix}$ (4)

式中:t为时间, τ 为时移, T₀是循环基频周期, n为循环频率谐波次数, N为循环频率谐波次数上界, R_x(t, τ )是循环自相关函数, 以T₀为周期, 将其展开为Fourier级数:

$\begin{matrix} \{\begin{matrix} R_{x} (t, τ) = \overset{\infty}{\sum_{n = - \infty}} R_{x}^{n / T_{0}} e^{j 2 πtn / T_{0}} = \sum_{α} R_{x}^{α} e^{j 2 παt} \\ R_{x}^{α} (τ) = R_{x}^{n / T_{0}} (τ) \\ = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} x (t + τ / 2) x^{*} \times (t - τ / 2) e^{- j 2 παt} dt \\ \leq x (t + τ / 2) x^{*} \times (t - τ / 2) e^{- j 2 παt} > t \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} R_{x}^{n / T_{0}} \end{matrix}$ 和 $\begin{matrix} R_{x}^{α} \end{matrix}$ 为离散化循环频率的自相关函数, α =n/T₀, 称为二阶循环频率, T为原信号x(t)的周期, 其他变量定义与公式(4)相同。公式(5)说明, 循环自相关函数可分解为一系列频率为α 的基函数, 只要在循环频率α 处, R_x(t, τ )≠ 0, 则x(t)在此频率处是二阶循环平稳的。

根据循环自相关函数, 可定义信号的循环谱 $\begin{matrix} S_{x}^{α} \end{matrix}$ (f)为循环自相关函数的Fourier变换, 即:

$\begin{matrix} S_{x}^{α} (f) = \int_{-\infty}^{\infty} R_{x}^{α} (τ) e^{- j 2 πfτ} dτ (6) \end{matrix}$ (6)

式中: $\begin{matrix} S_{x}^{α} \end{matrix}$ (f)为循环谱, $\begin{matrix} R_{x}^{α} \end{matrix}$ (τ )为循环自相关函数, τ 为时移, f为时移对应频率。它描述了被调制到循环频率α 上的信号的功率谱分布, 所以, 信号的载频和被调制分量频率通过相关谱的a~f分布被揭示出来。

4 谱相关对调幅信号的解调分析

对于一个调幅信号x(t), 定义其模型为:

$\begin{matrix} x (t) = A (1 + Bcos (2 π f_{b} t)) \cos (2 π f_{a} t + θ) \end{matrix}$ (7)

式中:A为载波幅值, B为调制系数, f_b为调幅频率, f_a为载波频率, θ 为载波初相位, t为时间。根据循环自相关函数的定义(5), 可得x(t)的循环自相关函数:

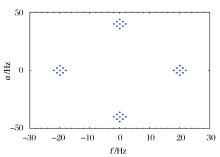
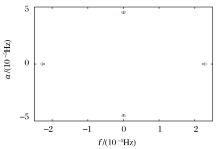
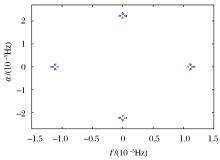
$\begin{matrix} R_{x}^{α} \end{matrix}$ (τ )= $\begin{matrix} \{\begin{matrix} \frac{A}{2} \cos (2 π f_{a} τ) |1 + \frac{B^{2}}{2} \cos (2 π f_{b} τ)|, α = 0 \\ \frac{A^{2} B}{2} \cos (2 π f_{a} τ) \cos (π f_{b} τ), α = \pm f_{b} \\ \frac{{(AB)}^{2}}{8} \cos (2 π f_{a} τ), α = \pm 2 f_{b} \\ \frac{A^{2}}{4} e^{\pm jθ} |1 + \frac{B^{2}}{2} \cos (2 π f_{b} τ)|, α = \pm 2 f_{a} \\ \frac{A^{2} B}{2} e^{\pm j 2 θ} \cos (π f_{b} τ), α = \pm (2 f_{a} \pm f_{b}) \\ \frac{{(AB)}^{2}}{16} e^{\pm j 2 θ}, α = \pm (2 f_{a} \pm 2 f_{b}) \end{matrix} \end{matrix}$ (8)

式中各个变量的含义与公式(7)相同。针对公式(7)描述的x(t)模型, 给定各参数如下:A=1, B=1, f_a=20 Hz, f_b=2 Hz, θ =0, 可得其相关谱如图1所示。

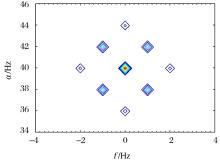
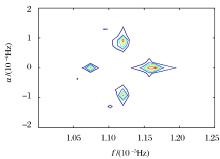
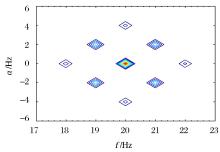
	Figure Option View Download New Window
	图1 调幅信号x(t)的循环谱Fig.1 The cyclic spectrum of x(t) modulated signal

从图1可以看出, x(t)的循环谱分布有4组谱点。由于循环相关谱的对称性, 仅分析其在正频部分的分布。首先选取循环频率α =0, ± f_b, ± 2f_b的功率谱分布放大(图2)。图2清晰显示出:当α =0时, 存在3个谱点, 频率f分别为:f_a, f_a + f_b, f_a-f_b, 对应于公式(8)中第一项; 当α =± f_b时, 存在2个谱点, 频率f分别为:(f_a + f_b)/2, (f_a- f_b)/2, 对应于公式(8)中第二项; 当α =± 2f_b时, 存在1个谱点, 频率f为:f_a, 对应于公式(8)中第三项。同样, 选取循环频率α =2f_a, 2f_a± f_b, 2f_a± 2f_b处的循环谱分布放大(图3)。图3清晰显示出:当α =2f_a时, 存在3个谱点, 频率f分别为:0, f_b, - f_b, 对应于公式(8)中第四项; 当α =2f_a± f_b时, 存在2个谱点, 频率f分别为:f_b /2, -f_b/2, 对应于公式(8)中第五项; 当α =2f_a± 2f_b时, 存在1个谱点, 频率f为0, 对应于公式(8)中第六项。

可见, 信号的循环相关谱清晰揭示出乘性调制信号的调制关系, 从循环相关谱还可以提取出载波频率和被调制波频率, 实现对乘性调制信号的解调。

	Figure Option View Download New Window
	图2 α =0, ± f_b, ± 2f_b处的循环谱分布放大图Fig.2 The distribution of the circular spectrum distribution at a=0, ± f_b, ± 2f_b

	Figure Option View Download New Window
	图3 α =2f_a, 2f_a± f_b, 2f_a± 2f_b处的循环谱分布放大图Fig.3 The distribution of the circular spectrum distribution at α =2f_a, 2f_a± f_b, 2f_a± 2f_b

5 基于EMD的循环平稳分析及其对重力固体潮信号的解调

EMD方法可以将信号自适应地分解为调频调幅波分量。为了对被分解出的调频调幅波实现乘性解调, 可对它们进行循环谱分析, 从而更清晰地揭示信号特征, 提取相关的特征参数。

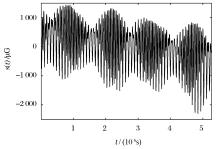
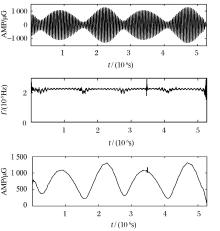
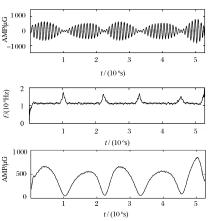
图4是一段在昆明地区测得的重力固体潮信号s(t), 该信号的采样频率为每小时一个样本点, 采样的时间长度为2个月。通过EMD分解, 得到2个主要模态分量(Instrinsic Mode Function)IMF1和IMF2, 其时频分布和时能分布分别如图5和6所示。由图5的时频分布可知, IMF1的调制频率为2.2352× 10^-5 Hz, 与重力固体潮的半日波(月亮主波)频率2.2364× 10^-5 Hz^[4]是一致的, 说明半日波分量已完整筛分到IMF1中, 同时, 由时能分布可知:在该半日波分量上调制有一个信号分量。同理, 由图6的时频分布可知, IMF2的调制频率为1.1584× 10^-5 Hz, 与重力固体潮的日波(太阳主波)频率1.1542× 10^-5 Hz^[4]是一致的, 说明日波分量已完整筛分到IMF2中, 同时, 由时能分布可知:在该半日波分量上也调制有一个信号分量。

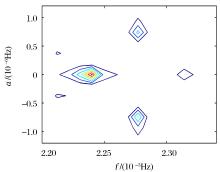
	Figure Option View Download New Window
	图4 重力固体潮信号Fig.4 Gravity solid tidal signal

为了解调出IMF1和IMF2中被调制的信号分量, 根据循环平稳分析理论的公式(5), 得到IMF1的循环相关谱如图7所示, 从图7中可知, IMF1的循环相谱对称分布有4个谱点, 为了清晰分析这些谱点的分布特性, 并考虑到其对称性, 选取其正频部分的分布放大如图8和图9所示。

在图8中, 首先分析在循环频率α =0上的分布(即IMF1的功率谱分布), 可以看出, IMF1在f=2.235× 10^-5 Hz和f=2.315× 10^-5 Hz处存在2个频点, 两频点间的间隔△ f=8.267× 10^-7 Hz, 与半月波(月亮赤纬波)频率:(8.472× 10^-7 Hz^[4])一致。同时可以看出, 在循环频率α =8.267× 10^-7 Hz上, 存在f=2.275× 10^-5 Hz的一个频点, 与半日波(月亮主波)频率:(2.315× 10^-5 Hz^[4])一致。

	Figure Option View Download New Window
	图5 信号IMF1及其时频分布、时能分布Fig.5 Signal IMF1 and time frequency distribution

	Figure Option View Download New Window
	图6 IMF2及其时频分布、时能分布Fig.6 Signal IMF2 and time frequency distribution

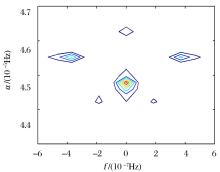
在图9中, 分析在频率f=0上的分布, 可以看出, IMF1在α =4.4× 10^-5 Hz和f=4.64× 10^-5 Hz处存在2个频点, 两频点间的间隔△ f= 16.534× 10^-7 Hz, 与2倍半月波(月亮赤纬波)频率一致, 同时可以看出, 在循环频率α =4.56× 10^-5 Hz(与2倍半日波频率一致)上, 分别存在f=± 4.134× 10^-8 Hz的2个频点, 与半月波(月亮赤纬波)频率的一半一致。

所以, 在IMF1分量中, 半月波(月亮赤纬波)频率为8.267× 10^-7 Hz, 被乘性调制到半日波(月亮主波)上, 基于半日波(月亮主波)频率2.275× 10^-5 Hz循环平稳。

IMF2的循环相关谱如图10所示, 从图10可知, IMF2的循环相关谱对称分布有4个谱点, 为了清晰分析这些谱点的分布特性, 并考虑到其对称性, 选取其正频部分的分布放大如图11和图12所示。同样的分析可知:在IMF2分量中, 半月波(月亮赤纬波)频率为8.267× 10^-7 Hz, 被乘性调制到日波(太阳主波)上, 基于日波(太阳主波)频率1.16× 10^-5 Hz循环平稳。

IMF1和IMF2在a~f域的这种分布同时说明:IMF1中, 半日波(月亮主波)分量和半月波(月亮赤纬波)分量的乘性调制是一种抑制载波的调制方式, 同样, IMF2中, 日波(太阳主波)分量和半月波(月亮赤纬波)分量的乘性调制也是一种抑制载波的调制方式。

	Figure Option View Download New Window
	图7 IMF1的循环相关谱Fig.7 Cyclic correlation spectra of IMF1

	Figure Option View Download New Window
	图8 IMF1的循环相关谱在α =0 Hz处分布Fig.8 The cyclic correlation spectra of IMF1 are distributed at α =0 Hz

	Figure Option View Download New Window
	图9 IMF1的循环相关谱在α =4.56× 10^-5 HzFig.9 Cyclic correlation spectrum of IMF1 at α =4.56× 10^-5 Hz

	Figure Option View Download New Window
	图10 IMF2的循环相关谱Fig.10 Cyclic correlation spectrum signal of IMF2

	Figure Option View Download New Window
	图11 IMF2的循环相关谱在α =0 Hz处分布Fig.11 Cyclic correlation spectrum of IMF2 at α =0 Hz

	Figure Option View Download New Window
	图12 IMF2的循环相关谱在α =2.24× 10^-5 Hz处分布Fig.12 Cyclic correlation spectrum of IMF2 at α =2.24× 10^-5 Hz

6 结论

EMD是一种实现信号自适应分解的信号分析方法, 但其分解得到的模态分量一般为调频调幅波, 为了从模态分量中解调出被调制分量和载波分量, 本文利用循环平稳的分析方法对EMD分解出的模态分量进行解调。仿真信号的分析结果显示:循环相关谱能揭示调制信号中调制分量和被调制分量的频率参数。将上述方法用于重力固体潮信号的分析, 完整提取出模态分量中的半日波分量、日波分量, 半月波分量频率参数。并揭示出:重力固体潮信号中, 半月波分量同时被调制到半日波和日波分量上。而且, 它们之间的调制方式体现为抑制载波的调制方式。以上结果说明:

(1) 通过对EMD模态分量的循环相关谱分析, EMD方法对信号的分解能力进一步提高, 既实现了对信号的加性分解, 也实现了对信号的乘性分解, 为信号的分析提供了一个完整的实现方案。

(2) 在重力固体潮信号中, 半日波分量和日波分量是加性叠加关系, 半月波分量与半日波分量之间、半月波分量与日波分量之间均是乘性调制关系, 这为深入理解重力固体潮信号中蕴含的物理信息具有参考意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Xu Houze. The Tides of the Solid Earth[M]. Wuhan: Hubei Science and Technology Press, 2010. 许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010. ] [本文引用:1]
[2]	Cui Yueju, Li Jing, Wang Yanyan, et al. Application of gas remote sensing technique to earthquake monitoring[J]. Advances in Earth Science, 2015, 30(12): 284-294. [崔月菊, 李静, 王燕艳, 等. 遥感气体探测技术在地震监测中的应用[J]. 地球科学进展, 2015, 30(12): 284-294. ] [本文引用:1]
[3]	Wu Qingchang, Zhou Zhi, Liang Hong, et al. AM-FM model of gravity tide IMF and its non-linear data fitting[J]. Computer Engineering and Applications, 2009, 45(30): 138-142. [吴庆畅, 周挚, 梁虹, 等. 重力固体潮IMF的AM-FM模型及其非线性拟合[J]. 计算机工程与应用, 2009, 45(30): 138-142. ] [本文引用:1]
[4]	Zhou Zhi, Shan Xiuming, Zhang Li, et al. The gravity tide of Kunming & Xiaguan based on the HHT[J]. Chinese Journal of Geophysics, 2008, 51(3): 836-844. [周挚, 山秀明, 张立, 等. 基于HHT提取昆明、下关重力固体潮的地震前兆信息[J]. 地球物理学报, 2008, 51(3): 836-844. ] [本文引用:6]
[5]	Huang N E, Zheng Shen, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society, 1998, 454: 903-995, doi: DOI:10.1098/rspa.1998.0193. [本文引用:2]
[6]	Zhao Hua, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society, 2004, 460(2 046): 1 594-1 611. [本文引用:1]
[7]	Huang N E, Man-Li C Wu, Long S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society, 2003, 459: 2 317-2 345, doi: DOI:10.1098/rcpa.2003.1123. [本文引用:1]
[8]	Huang N E, Shen Z, Long S R, et al. A new view of nonlinear water waves: The Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1993, 31: 417-457. [本文引用:1]
[9]	Zhao Jinping, Huang Daji. Mirror extend and circular spline function for empirical mode decomposition Method[J]. Journal of Zhejiang University (Science), 2001, 2(3): 247-252. [本文引用:2]
[10]	Gardner W A. Statistical Spectral Analysis: A Non-probabilistic Theory[M]. New Jersey: Prentice-Hall, 1987. [本文引用:2]
[11]	Garden W A. Spectral correlation of modulated signals: Part 1-analog modulation[J]. IEEE Transactions on Communication, 1987, 35(6): 584-594. [本文引用:1]
[12]	Garden W A. Exploitation of spectral redundancy in cyclostationary signals[J]. IEEE Signal Processing Magazine, 1991, 8(2): 14-36. [本文引用:1]
[13]	Gardner W A. The spectral correlation theory of cyclostaionary time-series[J]. Signal Processing, 1986, 11(1): 13-16. [本文引用:1]
[14]	Huang Zhitao. The Processing and Application of Cyclic Stationary Signals[M]. Beijing: Science Press, 2006: 23-26. [黄知涛. 循环平稳信号处理及应用[M]. 北京: 科学出版社, 2006: 23-26. ] [本文引用:1]
[15]	Gardner W A. Introduction to Rand om Processing with Applications to Signals and Systems(Second Edition)[M]. New York: McGraw-Hill, 1990. [本文引用:2]

2010

0.0

... 1 引言在太阳、月亮等天体的潮汐引力作用下,地球会产生沾弹性形变现象,反映这种现象的可观测地球物理信号是重力固体潮信号^[1] ...

2015

0.0

. 2015, 30(12):284-294 DOI:doi:10.11867/j.issn.1001-8166.2015.02.0284

Application of gas remote sensing technique to earthquake monitoring

遥感气体探测技术在地震监测中的应用

Cui Yueju , Li Jing , Wang Yanyan

崔月菊, 李静, 王燕艳

The principle of satellite hyperspectral remote sensing technique for atmosphere detection, development of the satellite atmospheric infrared sensors and the retrieval method of gaseous components with hyperspectral remote sensing data were briefly reviewed. The application of hyperspectral remote sensing gas-geochemistry in earthquake monitoring was emphasized, which can be divided into two aspects: ①Degassing from the seismic fracture zone was indirectly retrieved with the thermal infrared sensor; ②Gas-geochemical anomaly associated with the earthquake was directly detected by the atmospheric gas sensors. Gas-geochemical anomalies were obtained by correlating the physical and chemical anomalies caused by gas emission from the underground with the seismic activities. The possible mechanism of anomalies was discussed by analyzing the gas-geochemical anomalies related to the typical earthquake cases. Additionally, the developing aspects in seismic remote-sensing for gas-geochemistry were proposed.

扼要介绍了卫星高光谱红外大气遥感的原理,气体组分探测技术、反演技术和研究应用的发展历程,着重介绍了该技术在地震监测中的研究应用。遥感气体地球化学在地震监测方面的应用大致可以分为间接观测和直接观测2个方面：①利用卫星红外遥感间接监测地震断裂带脱气;②利用卫星探测大气成分的传感器直接监测地震前后的气体地球化学异常。通过分析地下气体逸散引起的物理化学异常与地震活动的关系,提取地震气体地球化学信息。介绍了典型震例的气体地球化学异常特征及其可能的形成机理,提出了存在的问题以及未来的研究重点。

... 这种重力潮汐的变化可以影响地壳应力的变化,积累大量的能量在地壳岩层中,以致触发地震^[2] ...

2009

0.0

. 2009, 45(30):138-142 DOI:doi:10.3778/j.issn.1002-8331.2009.30.043

AM-FM model of gravity tide IMF and its non-linear data fitting

重力固体潮IMF的AM-FM模型及其非线性拟合

Wu Qingchang , Zhou Zhi , Liang Hong

吴庆畅, 周挚, 梁虹

In this paper，the non-linear least squares data fitting method for the AM-FM model of the the gravity tide IMF signal is proposed.Firstly，the AM-FM model is decomposed amplitude modulation signal and frequency modulation signal which is fitted by using the non-linear least squares method separately.The fitting number is determined by the correlation coefficient.Then the IMF signal of the gravity tide is fitted by the AM-FM model.The experimental results show that the gravity tide IMF signal can be well described by the AM-FM signal.A foundation is established for further discussion its characteristic such as the cyclostationarity.

首先建立AM-FM数学模型，用多个相近载波的调幅信号组合描述它。利用最小二乘法对幅度调制和频率调制两个部分分别进行非线性拟合；拟合以相关系数满足一定条件为精度控制原则，拟合项数以相邻相关系数不再显著变化为判定条件。有效性检验证明该方法切实可行。重力固体潮IMF的拟合结果表明，AM-FM数学模型可以很好地刻画重力固体潮IMF；重力固体潮是多个AM-FM信号合成的复合信号。为后续深入研究重力固体潮的AM-FM信号特征、循环平稳信号特征等性质建立了良好的数学基础。

... 同时,重力固体潮信号反映了太阳、月亮等天体潮汐引力的周期变化,若能从重力固体潮信号中单独分离出各个天体的潮汐引力分量,揭示各分量间的叠加关系,将能更深刻的理解天体间重力作用规律^[3] ...

2008

0.0

. 2008, 51(3):836-844 DOI:doi:10.3321/j.issn:0001-5733.2008.03.024

The gravity tide of Kunming #cod#x00026; Xiaguan based on the HHT

基于HHT提取昆明、下关重力固体潮的地震前兆信息

Zhou Zhi , Shan Xiuming , Zhang Li

周挚, 山秀明, 张立

HHT time-frequency method is introduced in new analysis of gravity tide. Based on superiority of HHT, the character of gravity tide and nonstationary processes of earthquake, we design characteristic parameters of instantaneous frequency of gravity tide. And we refer to corresponding theoretical values of gravity tide in the course of earthquakes analysis. The results of Kunming and Xiaguan show that there are some premonitory changes in the characteristic parameters of instantaneous frequency before earthquakes, which bear short-term and synchronization characters. The characteristic parameters of instantaneous frequency have clear physical significance. These premonitory changes express that the nonstationary processes of earthquake influenced the observation of stationary processes of gravity tide.

在重力固体潮地震前兆分析中引入HHT时频分析新方法.结合HHT的优越性、固体潮的特点和地震的非平稳过程特性，设计重力固体潮地震前兆分析的瞬时频率特征参数；以相应理论计算值作为参照背景，研究固体潮的震前变化特征.昆明、下关的震例分析表明, 的确存在瞬时频率特征参数的震前变化，且具短期、同步正异常特征；瞬时频率特征参数具有明确的物理意义，其震前变化反映了地震非平稳过程对理论重力固体潮的影响.

... 从重力固体潮信号的产生机理可以看出,它是一个多周期的合成信号^[4] ...

... 为了反映这些分量之间的关系,文献^[4]中,引入EMD(empirical mode decomposition:经验模式分解)方法分析重力固体潮信号,得到了日波与半日波分量 ...

... 10^-5 Hz^[4]是一致的,说明半日波分量已完整筛分到IMF1中,同时,由时能分布可知:在该半日波分量上调制有一个信号分量 ...

... 10^-5 Hz^[4]是一致的,说明日波分量已完整筛分到IMF2中,同时,由时能分布可知:在该半日波分量上也调制有一个信号分量 ...

... 10^-7 Hz^[4])一致 ...

... 10^-5 Hz^[4])一致 ...

1998

0.0

... 但由于EMD分解所得的模态分量一般为调频调幅波^[5~9],所以,EMD分解所得的模态分量并未揭示重力固体潮信号中的乘性调制关系 ...

... 为了实现信号高分辨率的时频分析,Nordeng等引入EMD筛选方法^[5~9] ...

2004

0.0

2003

0.0

1993

0.0

2001

0.0

... 但由于EMD分解所得的模态分量一般为调频调幅波^[5~9],所以,EMD分解所得的模态分量并未揭示重力固体潮信号中的乘性调制关系 ...

... 为了实现信号高分辨率的时频分析,Nordeng等引入EMD筛选方法^[5~9] ...

1987

0.0

... 在循环平稳分析理论中^[10~15],循环相关谱描述了信号频谱间的乘性调制关系,据此,本文提出如下的信号分解方案:首先用EMD对信号进行加性分解,然后通过循环相关谱分析EMD模态分量的乘性调制关系,从而清晰揭示信号中各分量间的关系 ...

... 有一类特殊的非平稳信号,其统计特性随时间周期性的变化,即其统计特性是周期平稳的,称其为循环平稳信号,为了分析这类信号,建立了循环平稳理论^[10~15] ...

1987

0.0

1991

0.0

1986

0.0

2006

0.0

1990

0.0