作者简介:王磊(1991-),男,山东滨州人,硕士研究生,主要从事流域降水分布研究.E-mail:sdwanglei@lzb.ac.cn
高山区降水主要集中在湿季(5~9月),湿季小时降水的概率分布统计特征是研究山区降水分布的重要基础。选择祁连山中段典型流域为研究区,使用葫芦沟流域6个观测点2015年5~9月半小时降水数据,采用极大似然法对影响Γ分布函数的形状参数 α和尺度参数 β进行估计,并且对不同强度降水概率密度分布、累计概率密度以及降水概率与海拔和降水量关系进行分析。结果表明:形状参数 α和尺度参数 β呈明显负相关,形状参数α与小时平均降水量分布大致相同;在葫芦沟流域,除海拔因素外,局地地形也是影响降水再分配和降水概率分布的重要因素;在该流域,除降水事件增加外, 1~3 mm/h强度降水概率随着海拔增加而增加也是降水量随海拔增加而增加的主要原因。
The probability distribution of the wet season hourly precipitation is the important basis for the study of the precipitation distribution, especially in mountainous areas. Hulu watershed is the study area located in the upper reaches of Heihe River, Qilian Mountains. By adopting the maximum likelihood estimation, the shape parameter α and scale parameter β of 6 stations were obtained with observed wet season (May to September) half hourly data, and different intensity precipitation probability density distribution, cumulative probability density and probability of precipitation and elevation and precipitation relationship were analyzed. The shape parameter α and scale parameter β is significantly negatively correlated, shape parameter α and average hourly precipitation distribution is consistent. Local topography is also an important factor to affect the precipitation redistribution and the probability distribution of precipitation in Hulu watershed. In addition to the increase of precipitation events, the probability of 1~3 mm mm/h precipitation increases with the altitude, which is the main reason for the increase of precipitation with altitude.
降水是水循环中的重要环节, 决定着一个地区的水热状况, 是流域水量平衡、水分循环、区域水资源评价、分布式水文模型的重要输入参数[1, 2]。我国西北干旱区径流的主要来源是山区降水, 但复杂的山区地形和局地小气候形成了复杂多变的降水时空分布格局[3], 使得山区降水在短时间尺度上没有明显的统计规律, 成为获取山区高精度降水资料的瓶颈。因此, 短时间尺度上的降水量概率统计特征成为解决该问题的关键, 成了学者研究的热点话题[4, 5]。国内外学者通过多种方法对降水量概率统计特征进行了研究, 特别是Γ 函数在降水量概率统计中取得不少成果。Vlĉ ek等[6]证明了Γ 函数基本上可以模拟区域日降水量概率的分布特征。Watterson等[7]利用Γ 函数的形状参数和尺度参数变化规律对全球日降水和极端降水概率进行分析, 指出大强度降水多发生在热带地区, 小强度降水多发生在副热带地区, 且预测副热带地区平均日降水量到2071— 2100年将增加约7%。丁裕国[8]利用20多个观测站的月降水量概率和Γ 函数、正态分布、Weibull分布、Kappa分布模拟比较, 证明了Γ 函数对降水量概率分布研究具有普遍适用性。田付友等[9]对我国极端降水事件进行预估并指出四川盆地西南地区降水强度主要集中在5 mm/h以下; 而华南沿海、海南西北部、鲁豫皖交界处短时强降水发生较多, 降水强度超过10 mm/h的概率超过10%。吴洪宝等[10]对广西6, 7月最大日降水量进行了概率统计, 研究表明Γ 函数克服了用样本频率代替概率不可避免的随机振荡, 用于拟合10和20天内最大日降水量概率分布更为合理。理论和实践证明Γ 概率密度分布函数可用于模拟不同区域、不同时间尺度的降水量概率分布特征。
祁连山区海拔3 000~6 000 m, 受地形和高寒条件的限制, 高海拔山区的气象站稀疏且主要分布在海拔相对较低的平坦地区, 且高海拔山区海拔落差大、地形复杂, 降水的时空分布具有很大的变异性[11, 12], 极大地制约了高海拔山区精确降水数据的获取。如何利用有限的观测数据应用于降水量概率特征研究, 进而服务于以降水为数据基础的相关学科研究, 成为备受重视的科学问题。目前祁连山区黑河流域的水文气象站主要集中在海拔3 500 m以下中低山带。研究工作多是基于这些气象站的数据, 但最新研究表明, 3 500 m以上山区降水量随海拔增加依然在增加[13, 14]。由于大部分高海拔山区降水相关研究选用的观测点海拔相对较低, 缺乏高海拔山区降水数据, 研究结果应用存在一定局限性。为此本文选取祁连山葫芦沟流域的一条典型剖面的6个观测点, 分析不同海拔高度山区降水量概率分布特征, 从而对流域内降水分布有一个整体认识, 为祁连山黑河上游山区水资源形成、径流模拟以及科学水资源管理提供重要的基础资料。
葫芦沟流域位于祁连山北坡黑河上游, 地处99° 50'~99° 54'E, 38° 12'~38° 17'N, 流域面积23.1 km2, 海拔2 960~4 820 m, 垂直高差1 860 m。研究区位于山区湿润气候和山前荒漠交界处, 受西风带、夏季风和高原季风的综合影响[13]。流域内东西两支河流在流域中部交汇, 形成‘ Y’ 字形山谷, 开口朝北, 便于水汽聚集, 南部有高大山体阻挡, 水汽被迫抬升形成降水。降水复杂多变, 阵性降水时有发生, 年均降水量约为495.1 mm, 主要集中在湿季(5~9月), 占全年降水量80%~93%[15]。本文所选剖面与流域内东支河流基本平行, 是典型迎风坡, 降水梯度变化明显, 最大海拔落差1 518 m。独特的地理特点、相对充沛的湿季降水以及巨大的海拔落差为研究山区不同强度降水概率分布特征提供了优良的研究条件。流域内6个观测点依据海拔梯度和主风向布设(表1), 每个观测点架设一个自动气象站, 每半小时对降水(TRwS504)、温度(HMP45D)、风速(LISA/RITA)等常规观测项记录一次。文章使用2015年5~9月半小时间隔的降水、温度和风速资料, 对不同强度降水分别进行概率统计。
| 表1 葫芦沟流域降水观测点信息 Table 1 Introduction of precipitation observation points in Hulu watershed |
降水校正公式是陈仁升等[16]依据世界气象组织(WMO)2种标准:降雨标准坑式雨量筒和双层栅栏降雪对比标准, 将葫芦沟流域2010年9月至2015年4月观测的608次降水事件分别与2种标准对比分析后得出, 主要依据温度对固态、液态、固液混合降水划分并分别校正, 该区域雨雪临界气温为0 ℃和3 ℃[16]。
Γ 分布是气候统计学中重要的偏斜分布, 可以拟合包括降水在内的多数正偏分布, 在气候统计学中应用广泛。张耀存等[17]提出降水量概率分布Γ 通用模式, 丁裕国[8]使用上海1873— 1982年6月的降水数据, 用不同方法对降水量概率分布进行拟合, 证明了Γ 分布的概率密度函数是研究降水量概率分布的最优方法。上述研究中以降水日数为研究样本, 缺点在于误差较大, 例如, 滇西北的德钦和滇南的思茅, 两地年平均降水日数分别为165.7天和165.3天, 但是实际年平均总降水时数分别为2 237小时和909小时, 相差2.5倍[18]。因此用小时表示样本总量大大缩小了各观测点之间的统计误差, 文章选用Γ 函数对研究区内不同强度小时降水进行概率统计, 分析可能存在的规律。Γ 分布的概率密度函数为:
式中:α 和β 分别为形状参数和尺度参数, Γ (x)是Γ 的函数, 表达式为:
α 是公式(2)中的唯一变量, 确定α 即有唯一的Γ (t)与之对应, Γ 分布的概率密度函数也将唯一确定。α 和β 的计算方法有2种, 分别是距估计法[19]和极大似然法[20, 21]。由于距估计法不能充分利用所有样本信息, 而且当α 较小时, 模拟结果严重偏离实际[22, 23]。本文使用极大似然法对参数α 和β 进行计算, 极大似然法表示为:
即首先得到降水样本均值的自然对数和样本自然对数均值的差y, n是各站点记录的小时内出现降水的样本总量。那么形状参数α 和尺度参数β 即可由公式(3)和公式(4)求出。其中α 单位与样本单位相同, β 无量纲。求得形状参数α 和尺度参数β 后, x变成Γ 分布的概率密度函数唯一变量, 因此可以求出任意降水阈值区间的降水概率:
式中: ∫0+∞ f(x)=1; a, b分别表示已知的降水阈值区间。相反, 如果知道了降水量累积概率P和初始累计下限a, 通过公式(6)便可求得上限降水量阈值。该方法可以对实际降水观测中的极端降水事件进行预估, 为气象预报业务提供参考。
Γ 函数的分布形态受形状参数α 和尺度参数β 控制。由文献[24]可求得描述降水分布的偏度系数r=
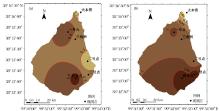
6个站点的具体参数如表2所示, 各参数存在明显的站点差异。整体而言, 形状参数α 在0.6~1变化, 且α 的均值为0.763, 形状参数α 值总体较小, 高海拔山区小时降水量强度较小[9, 26]。最小值出现在二号点, 最大值出现在四号点。说明二号点降水量分布偏度较大, 二号点出现最小值的原因可能是:二号点背面山体陡峭, 水汽受山体阻挡, 多发生阵性降水, 而这些阵性降水强度较小; 四号点降水量偏度较小, 相对其他观测点不同强度降水较分散。大本营的α 值同样较小, 因为该观测点海拔较低, 小强度降水占有比重较大。图1所示, 二号点(b), 大本营(e)大于1 mm/h降水明显比其他观测点少。此外, 如图2中, 形状参数和小时平均降水量分布大致相同, 一号点、四号点均处于高值区。除二号点以外, 其他各点形状参数和小时平均降水量基本上随着海拔的升高而增加, 即高海拔区域出现较强小时降水的概率更大。图2(b)中大本营附近等值线相对密集, 因为该观测点到一号点附近坡度较小, 地势相对平坦, 小时降水量变率较小。三角洲、二号点、三号点、四号点之间等值线相对稀疏, 主要是观测点之间海拔梯度较大, 地形复杂, 降水变率较大。尺度参数β 在1.1~1.6变化, 最小值是四号点的1.137, 最大值是二号点的1.534。二号点不同强度降水概率密度分布集中, 阵性降水多是小强度降水。此外, 尺度参数β 与形状参数α 比较来看, 基本上与其变化基本成负相关, 与相关研究有类似结论[9]。
| 表2 各观测点参数特征 Table 2 Parameter characteristics of each observation point |
为了在空间和时间上对不同强度降水发生的概率进行分析, 将各个站点降水强度分为< 1, 1~2, 2~3, 3~4, 4~5, > 5 mm/h分别进行概率统计。由于地形效应[27, 28], 局地地形成为影响降水分布的重要因素[29]。图1灰色柱状图为观测的不同强度降水发生频率, 函数曲线为Γ 概率密度函数拟合频率。对模拟与观测之间的分布情况进行对比发现二者有很好的相似性, Γ 分布概率密度函数精准的模拟了不同量级降水量概率。总体而言, 如图1所示, 各个观测点的Γ 函数相似, 样本频率明显偏态分布, 强度越小的降水发生的概率越大, 样本频率和Γ 概率密度函数拟合曲线均呈反J形, 与部分学者对降水概率分布研究结论一致[8, 9, 17, 30]。6个观测点小时降水量多在1 mm以下, 小于1 mm/h量级降水均占到降水样本总量的60%以上。在四号点所占比重最小, 但是四号点发生小时降水样本总量最大且小时降水量均值最高, 相比其他观测点, 该点降水相对分散。三角洲、二号点均达到70%, 虽然2点海拔落差较大, 但是周围地形相似, 两者背面均有陡峭山体阻挡, 容易发生强度较小的阵性降水。强度小于2 mm/h降水, 占到所有降水样本80%以上。当降水强度阈值增加为3 mm/h时, 累计概率均超过了90%, 即90%以上小时降水量都在3.0 mm以下。因此, 对于葫芦沟流域而言, 多数小时内降水强度小于3 mm/h, 出现小时内大强度降水概率较小。
观测点观测降水量概率累计与Γ 概率密度函数累计对比可知(图3):一号点、三号点、大本营3个观测点拟合曲线与实际观测曲线基本重合, 与3个观测点附近地形有关, 3个观测点周围没有高大山体, 比较开阔, 由地形造成的局地降水很少发生。三角洲、二号点、四号点3个观测点的拟合情况相似, 小时降水量在小于3 mm范围内, 模拟累计频率低估了观测累计频率。这3个观测点周围都有高大山体, 受山体影响局地阵性降水发生频率较大, 阵性降水强度较小, 这可能是观测累计频率大于模拟累计频率的原因。当小时降水量超过3 mm时, 模拟累计概率高估了观测累计概率。
由于高海拔山区的生态环境脆弱性和极端降水的致灾性和破坏性, 学者越来越关注山区极端降水分布特征。多数学者将极端降水定义为超过某一概率阈值的降水事件, 一般取阈值为90%或95%[31, 32]。本文取阈值90%, 将小时降水量累计概率超过90%的降水量定义为极端小时降水。根据公式(6)求得不同累计概率下的降水量, 各观测点对应不同概率下降水量阈值如表3和图4所示。不同累计概率条件下各观测点降水阈值大致随海拔增加而增加, 但是三角洲、二号点、四号点并不完全遵守这一规律, 因为3个观测点附近地形复杂, 降水分布明显受到地形的影响。三角洲在所有累计概率下的降水量阈值相对偏小; 二号点在70%以下累计概率条件下降水阈值偏小, 70%以上累计概率降水量阈值恢复正常; 四号点在70%以上累计概率时降水量阈值明显变小。70%的累计概率的降水阈值大致为1 mm/h, 即三角洲、二号点相比其他观测点, 强度小于1 mm/h降水较多, 四号点强度大于1 mm/h降水对于所在海拔高度来讲相对偏少, 不同强度降水量概率分布与局地地形有显著关系。各观测点极端降水最大阈值和最小阈值分别出现在三号点和大本营, 小时降水量分别为2.776 mm和2.087 mm, 这意味着三号点出现大强度降水的概率大于四号点, 在短时间尺度上, 局地地形成了影响降水再分配的重要因素[27]。葫芦沟流域60%的小时降水量小于1 mm, 超过90%小时降水量为0~3 mm, 即小时降水量超过3 mm的概率不到10%。虽然该流域发生短时强降水概率不大, 但是部分地区土质疏松, 碎石较多, 一旦发生短时强降水极易造成滑坡等自然灾害。2013年6月7日, 小时降水量达到16.8 mm, 造成严重滑坡、泥石流灾害, 数家牧民牧场、临时住房以及流域出口水文断面观测点冲毁, 造成严重经济损失。因此对极端降水做好预报工作是防灾减灾的重要基础, 尤其是在容易发生灾害的高海拔山区。而Γ 分布概率密度函数能很好地模拟不同区域降水量发生概率, 对指导不同区域防灾工程建设有重要意义。
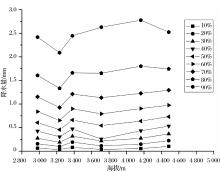 | 图4 各观测点不同累计概率下小时降水阈值折线图Fig.4 Precipitation threshold line chart of each observation point under different cumulative probability |
| 表3 不同累计概率下降水阈值统计特征(单位:mm) Table 3 Statistical characteristics of precipitation threshold under different cumulative probability (unit:mm) |
在山区, 由于不同强度降水概率明显受海拔[13, 18]和降水量[9]影响, 分别对小时降水强度小于1 mm, 1~2 mm, 2~3 mm降水概率与海拔、降水量关系进行了拟合(图5), 不同强度降水概率随着海拔、降水量增加变化明显。一般而言, 山区降水量随着海拔的增加而增加, 葫芦沟流域年降水量变化梯度约为200 mm/km[14]。随着海拔增加降水量增加的同时, 不同强度降水概率会明显变化。强度小于1 mm降水发生概率随着海拔和降水量增加呈减小趋势, 梯度约为-0.06 km-1(图5a)和-0.0004 mm-1(图5b); 强度为1~2 mm的降水概率随着海拔和降水量增加呈增加趋势, 梯度约为0.04 km-1(图5a)和0.0002 mm-1(图5b); 降水强度为2~3 mm降水发生概率梯度值分别是0.01 km-1(图5a)和0.00001 mm-1(图5b)。其他强度降水随着海拔和降水量的变化而变化不大, 即这些强度降水在各站点发生概率基本上相同。可以看出, 强度小于1 mm的降水概率随海拔明显减少, 但是降水量依然随着海拔的增加。因此在该区域, 除降水样本总量增加外, 小时降水强度为2~3 mm的降水发生概率随海拔的增加而增加也是主要原因。
(1) Γ 函数中形状参数α 和尺度参数β 存在负相关关系, 而且形状参数α 值与所处地形有关, 基本上与海拔成正比。此外形状参数与小时平均降水量分布大致相同, 高值区主要集中在一号点和四号点。
(2) Γ 分布概率密度函数可以很好地描述出实际观测小时降水量的概率分布情况, 并且通过Γ 分布概率密度函数还可以对区域不同概率下所保证降水量情况进行估算。葫芦沟流域观测数据证明, 除海拔因素外, 局地地形也是影响降水再分配和降水概率分布的重要因素。
(3) 降水量随着海拔的增加而增加, 不仅因为降水事件增加, 大强度降水概率增加也是主要原因。其中强度小于1 mm/h降水发生概率随着海拔和降水量增加呈减小趋势, 梯度约为-0.06 km-1和-0.0004 mm-1; 强度为1~2 mm/h的降水发生概率随着海拔和降水量增加呈增加趋势, 梯度约为0.04 km-1和0.0002 mm-1; 降水强度为2~3 mm/h降水发生概率梯度值都是0.01 km-1和0.00001 mm-1。其他强度降水随海拔变化概率不大。
概率预报是我国强对流预报中面临的新挑战, 尤其是在降水变率大的高海拔山区, 对实地观测资料的小时降水量概率分布研究是概率预报的敲门砖。为此, 在下一步研究中收集更多高海拔站点和高质量长时效降水数据, 研究基于Γ 分布的日降水量、月降水量的概率统计变化特征, 进一步研究Γ 分布在概率统计甚至气象预报中的适用性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|