地表温度(Land Surface Temperature, LST)是全球和区域气候变化以及地表与大气水分和能量交换的重要指示因子, 广泛应用于天气预报、林火监测、资源勘探、极端灾害监测、水资源利用和城市气候监测等方面^[1~3]。自20世纪80年代以来, 卫星遥感反演高精度LST一直是定量遥感研究领域的重点内容之一^[4]。目前基于卫星热红外数据反演LST的理论和方法已趋于成熟, 并已有相关业务化产品, 如美国宇航局(National Aeronautics and Space Administration, NASA)发布的MODIS(Moderate-Resolution Imaging Spectroradiometer)LST产品^[5]、欧洲气象卫星应用组织(European Organisation for the Exploitation of Meteorological Satellites, EUMETSAT)的SEVIRI(Spinning Enhanced Visible and Infrared Imager)地表温度产品^[6]、欧洲空间局(European Space Agency, ESA)的AATSR(Advanced Along-Track Scanning Radiometer)LST产品^[7]等。这些LST产品有力推动了陆面过程和全球与区域气候变化研究。

LST作为许多陆面模型的输入参数, 对模型输出结果有较大影响。例如, 在地表蒸散发模型中温度误差1~3 K则会显著影响模型结果, 可能导致模型估计值达100 W/m²的误差^[8]。因此, 卫星遥感LST的验证及其结果, 不仅对于用户在实际应用中非常重要, 同时也有助于LST反演算法和生产系统的改进。目前, 地表温度遥感产品的验证方法包括基于实测LST的直接验证, 基于辐射传输正向模拟的间接验证, 以及不同地表温度产品的交叉比较。其中, 利用实测的LST与对应像元反演LST进行对比的直接验证是应用最广泛也最重要的地表温度验证方法^[4]。实测LST主要通过四分量净辐射传感器(或长波辐射传感器)或红外辐射计获得, 测量方式为单点测量、剖面线测量、流动测量或无线传感器网络面状测量等。然而, 地面站点测量值与卫星像元之间可能存在显著的空间尺度不匹配。更重要的是, 在自然地表中LST可能在亚像元尺度上显著变化^[4]。在均质下垫面(如沙漠、湖泊等)采用像元内若干个地面站点测量值的平均值作为像元真值代表值可能是合适的^[9], 但对于大量存在的异质性下垫面, 采用地面单点测量值或少数点测量值的平均值作为验证基准, 则存在较大的不确定性。长期以来, 尺度转换问题一直是定量遥感领域基础而重要的科学问题之一^{[10, 11]}。在异质性下垫面如何将地面单点测量值升尺度到目标卫星像元尺度并作为LST验证的相对真值始终是一个难题^[12]。同时, 由于受到宏观尺度上地表三维结构和微观尺度上组分发射率的影响, 遥感获取的异质性下垫面LST具有方向性变化, 并随着下垫面异质性程度具有显著变化, 这也给遥感LST验证带来困难^[13]。

异质性下垫面是指目标区域内有多种不同的地表覆盖类型组成的地表。按照空间分布方式的不同, 异质性下垫面可分为二维平面异质性下垫面(如裸土和草地交错)和三维空间异质性下垫面(如稀疏林地、起伏地形等)。三维空间异质性下垫面相对于二维平面更加复杂。由于受太阳光照方向— 地面— 传感器观测方向几何关系和地表三维结构的影响, 传感器观测LST呈现出观测方向性效应。因而三维空间异质性下垫面, 特别是稀疏林地地表, 一直是像元尺度地表温度相对真值研究的难点^[14~16]。获取像元尺度的LST相对真值对量化遥感反演的LST产品的不确定性是十分必要的^{[17, 18]}。由于异质性下垫面在全球地表面积中占有相当大的比重, 异质性下垫面像元尺度LST相对真值获取困难, 导致遥感反演的LST产品不确定性难以准确评估, 这严重制约了LST产品的深入应用^[14]。

对于稀疏林地这类异质性下垫面而言, 其地表温度相对真值获取的关键在于通过场景模型来确定组分比例。按照模型是否需要真实场景建模, 本文将异质性下垫面像元尺度LST模拟的主要模型方法分为3种:修正几何投影模型、真实结构三维模型以及其他模型。本文归纳了各种异质性下垫面像元尺度LST相对真值获取的模型方法, 指出了尚待研究的主要问题, 并探讨了未来的发展方向。

由于地表并不是黑体, 根据斯忒藩— 玻尔兹曼定律, 地表辐射出射度M为:

M=εσTs41

式中:M的单位为W/m²; ε 为地表宽波段发射率; σ 为斯忒藩— 玻尔兹曼常量, 取值为5.67× 10^-8 J/(s· m²· K⁴); T_s为地表温度。

由于传感器硬件制作工艺等原因, 目前卫星热红外遥感获取的LST的像元空间分辨率多为百米级至公里级, 属于中低分辨率, 其像元多为混合像元。而地面测量难以直接获取如此大的空间范围, 因此需要将地面单点测量值升尺度到目标卫星像元, 得到卫星像元地表温度的相对真值。对于稀疏林地, 根据地表覆盖类型和阴影情况, 一般将组分类型分为光照植被、阴影植被、光照裸土和阴影裸土4种。假设像元总的辐射出射度为像元内部各组分辐射出射度的加权和^[19]:

Lpixel=∑Lifii=1n(2)

式中:L_pixel为传感器接收到的地面发射总辐射; L_i, f_i分别为像元内各组分发射辐射和组分比例, 其组分比例之和为1; n为混合像元包含的组分数目。

假设同种组分内部温度分布均匀, 模拟像元地表温度T_pixel定义为:

Tpixel=∑i=0nεifiTi4ε3

式中:ε _i为组分发射率, 其可通过地面实测获取; T_i表示异质性下垫面像元内组分温度, 其可通过地面实验或者高分辨率机载热红外数据获取; ε 为混合像元的混合发射率, 假设其是像元内各组分类型发射率的线性加权^[19]:

ε=∑i=0nεifi4

公式(3)表明, 异质性下垫面像元尺度地表温度主要与发射率、像元内组分比例和组分温度密切相关。一般情况下, 各组分并非朗伯体, 其发射率具有各向异性特征。但发射率的各向异性研究非常困难, 大多数研究假定其为各向同性^{[16, 19]}。因此, 混合像元地表温度模拟的主要前提是准确获取像元内各组分比例。

异质性下垫面LST受到地表空间异质性、光照方向— 地面— 传感器观测方向几何关系以及时间和季节变化等多种因素影响。有研究根据植被指数、土壤湿度等与LST有关的指示因子对遥感反演的大尺度LST进行降尺度, 从而与单点实测数据进行温度比较。这在一定程度上能减小由于尺度效应造成的验证误差。但是由于受到地面空间异质性^[20]、传感器视场角^[21]、光照方向— 地面— 传感器观测方向几何关系^[19]的影响, 这种方法仍然存在空间尺度和视场范围不匹配以及方向性效应等问题, 在稀疏植被区该问题显得尤为突出^[18]。

异质性下垫面像元尺度LST模拟的实质就是像元尺度LST相对真值的获取, 该过程主要目标是实现地面实测单点温度向目标像元尺度的转换。通常将目标像元按照地物类型和光照阴影情况分为光照裸土、阴影裸土、光照树冠和阴影树冠4种基本组分类型。假设传感器接收的总辐射量是场景中各组分辐射量的投影面积比例加权, 同种组分类型内部温度分布均匀^[19]。

3.1 修正几何投影模型

Pinheiro等^[14]在几何光学模型的基础上发展了修正几何投影模型(Modified Geometric Projection Model, MGP)。模型结合了几何光学模型和热辐射原理。在MGP模型中, 树冠被简化为椭球体, 场景中树冠内部的空隙采用叶面积指数(Leaf Area Index, LAI)来量化, 计算树冠总的空隙所占的面积。树冠在场景中服从统计学分布, 如双泊松分布^{[22, 23]}, 运用布尔模型计算树冠间的空隙率^[24]:

qθ, ϕ=e-ζA̅θ, ϕ5

式中:ζ 为场景中树冠单位面积的平均密度^{[25, 26]}, 单位为m^-2; θ 为考虑的天顶角; ϕ 为考虑的方位角; A̅(θ , ϕ )为树冠从(θ , ϕ )方向投影在平面地面上的平均面积, 单位为m²。

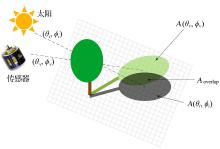
采用几何光学模型计算场景中树冠的各组分比例(图1), 光照裸土组分比例K_g、阴影裸土组分比例K_z、光照树冠组分比例K_c和阴影树冠组分K_t比例分别如下^[27]:

Kg=e-ζ[A̅(θi, ϕi)+A̅(θv, ϕv)-O(θi, θv, ϕi, ϕv)] (6a)Kc=121+cosψ1-e-ζA̅θv, ϕv(6b)Kt=121-cosψ1-e-ζA̅θv, ϕv(6c)Kz=e-ζA̅(θv, ϕv)-Kg6d)

式中:O(θ _i, θ _v, ϕ _i, ϕ _v)表示树冠在太阳光照方向(θ _i, ϕ _i)和传感器观测方向(θ _v, ϕ _v)分别投影到平面地面的重叠区域面积; cos ψ =cos θ _s cos θ _v+sin θ _s sin θ _v cos ϕ _i-v; ϕ _i-v为光照方向与观测方向的相对方位角。

图1

Fig.1

	Figure Option ViewDownloadNew Window
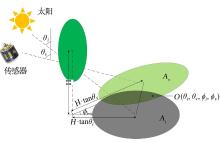	图1 太阳光照阴影和传感器观测阴影的相互关系[28]Fig.1 The relationship between the actual shadow on the ground and shadow observed by the satellite sensor[28]

由于遥感反演的LST随观测角度不断变化, 因而在LST产品应用中需要将极轨卫星获取的长时间序列的LST数据集校正到一个具体的角度。Pinheiro等^[14]利用极轨卫星宽视场角(传感器视场角± 55° )传感器AVHRR(Advanced Very High Resolution Radiometer)反演的LST研究了其包含的系统误差与光照方向— 传感器观测方向几何关系的相关性。对1995— 2000年非洲大陆的LST分析表明, 地表温度方向性观测差异最大达到9 K。MGP模型也为遥感传感器观测的LST的方向性校正提供一种思路。Pinheiro等^[19]在非洲南部的热带稀疏大草原对MGP模型进行了验证。模型与高精度的离散各向异性辐射传输模型(Discrete Anisotropic Radiative Transfer, DART)进行比较, 两者模拟LST相差小于1 K。MGP模型模拟值与地面塔的实测LST比较表明, 两者差值小于2%。Rasmussen等^{[15, 29]}利用MGP模型研究静止气象卫星MSG(Meteosat Second Generation)上的SEVIRI传感器反演的LST对观测角度的依赖性。模拟的SEVRI实际观测方向的LST和星下点方向的LST最大差值超过6 K。因此, 在对不同传感器反演的地表温度进行比较和使用时, 需要考虑地表温度的观测的方向性效应。

MGP模型在计算组分比例中的O(θ _i, θ _v, ϕ _i, ϕ _v)较为复杂, Ermida等^[16]对MGP模型做了改进。运用微积分的思想将投影平面划分为0.01 m的规则网格(图2), 采用计算机计算单棵树冠投影到地面上的投影面积A(θ , ϕ )和树冠在传感器观测方向与太阳光照方向在地面上投影的重叠区域面积A_Overlap。改进后模型与原始MGP模型相比, 两者模拟LST差值小于0.25%。该方法被用于SEVIRI和MODIS LST的比较。原始MGP模型局限于计算简单树冠形状, 如锥体、球体等, 对复杂地面场景及人工地表无法有效表达, 而经Ermida等^[16]改进后的模型能适应各种树冠形状。MGP模型中假设场景中地面只有裸土一种类型, 而实际地表情况可能十分复杂。Cao等^[30]考虑场景中道路的影响, 将场景分为道路区域和农作物区域分别计算两者对整个混合像元地表温度的贡献, 同时考虑了道路周围农作物对道路的影响。利用黑河流域的机载热像仪数据验证了模型误差小于1.1 K。与原始MGP模型相比, 该模型对特定场景的处理更加细致。

MGP模型作为一种简单、输入参数少、具有相对严谨物理意义的地表温度升尺度方法, 能够用于自然地表异质性下垫面像元尺度地表温度相对真值的模拟。正是由于该模型的这些特性, 使得其特别适合模拟全球或者大范围区域LST。但是, 由于模型没有考虑树冠间的多次散射效应, 以及对复杂场景的简化, 这些使得模拟精度难以达到辐射传输模型的精度。同时由于模型采用平行光线投影, 难以模拟球状空间。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 在光照— 观测几何条件下投影到规则格网上的面积图示[16]Fig.2 Schematic diagram of projected areas on the fine regular grid under a given illumination and viewing geometry[16]

3.2 真实结构三维模型

3.2.1 离散各向异性辐射传输模型

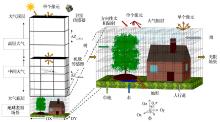
DART是一种严格的、高级的辐射传输模型。该模型于1992年由CESBIO(Centre d’ Etudes Spatiales de la BIOsphè re)实验室提出^[31]。DART模型不但能够在异质性三维结构植被覆盖地表估计短波和长波范围的辐射传输, 而且可以估计窄波段甚至整个光谱范围的表面方向辐射和热量分布。在近地表空间, 整个场景被分为大小相等的立方体单元。场景主要类型包括:裸土、树叶、树干、草地、水体等。模型假设裸土、树干是不透明介质, 树叶是浑浊介质, 树叶内部存在多次散射。在场景所在的4π 空间内, 按照设定的方向数目N, 将4π 空间离散为N个方向, 根据光线跟踪计算每个立方体单元沿着各个方向的发射辐射和散射。场景中树冠位置和大小可以是随机分布、统一大小, 也可以根据实际空间分布设置。模型输入参数包括LAI、树冠形状和高度、地形参数、场景温度分布、叶子的光学特征等。模型经过不断改进增加了更多的地表要素, 如建筑物等, 从而使模型更加逼真(图3)。

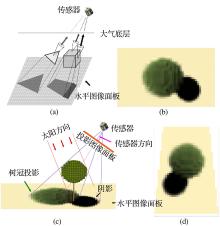
Guillevic等^[33]将DART模型扩展到热红外领域用于解释树冠结构对方向性观测亮温的影响。DART模型用于计算传感器在特定观测方向获取的地面混合场景的组分比例, 结合热辐射原理, 采用地面实测组分温度数据线性加权得到混合像元温度值。模型模拟值与行种棉花冠层实测亮温间的比较结果表明, 模型具有较高的模拟精度, 均方根误差小于1.2 K。Guillevic等^[13]利用该模型检验极轨卫星传感器MODIS在稀疏植被区反演的LST的数据质量。同时, 利用该模型作为尺度转换和角度校正工具对极轨卫星传感器MODIS与静止轨道卫星传感器SEVIRI反演的LST分析表明, 两者温度方向性差异最大可达12 K。Yin等^[21]对DART模型进行了改进, 模型增加了透视投影(图4)。改进后的模型能够适用于各种传感器角度和视场类型, 丰富了模型应用范围。DART模型考虑了辐射的多次散射效应, 因而模型精度高。但是, 模型输入参数较多, 计算时间复杂度大, 地面高精度快速建模困难, 这些因素限制了模型的使用范围。因此, 模型适合小范围、精确模拟。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 DART模型系统图示[32]Fig.3 Schematic diagram of the DART model[32]

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 DART模型透视投影图示[21]Fig.4 Schematic diagram of the DART perspective projection[21]

3.2.2 地表— 传感器— 太阳关系模型

地表— 传感器— 太阳关系模型(The Surface-Sensor-Sun Relations Model, SUM)是一种基于辐射度方法的表面真实结构三维模型。Soux等^[34]利用该方法获取了传感器视场内的城市表面组分比例。模型中城市建筑物按照一定的大小和间距排列, 场景表面被细分为三角面元。SUM模型采用了计算机辐射度方法中的形状因子计算组分比例, 获取每个传感器可视面元对传感器的辐射贡献比例。Voogt^[35]在加拿大温哥华进行了航空飞行试验, 并对SUM模型进行了改进。城市表面建筑位置、大小和高度均采用实际大小, 场景更加逼真。周纪等^[36]、占文凤等^[37]和马伟等^[38]在北京师范大学房山试验场基于SUM模型构建的城市三维结构缩小模型, 模拟了城市区域热辐射方向效应的时空特征, 并分析了传感器的视场效应。研究指出, 近地面宽视场角传感器观测值与卫星观测值比较时, 需要考虑近地面传感器的视场效应^[39]。SUM模型由于采用辐射度方法中的形状因子计算组分比例, 获取的组分比例相较于平面投影精度更高^[40]。模型忽略了多次散射效应, 因此适合模拟建筑等辐射发射难以穿透的介质。由于模型计算量与面元数量正比, 场景较大、面元细分大小越小则计算耗时越长。因而该模型适用于小范围精确模拟。

3.2.3 热辐射— 图像混合模型

辐射— 图像混合模型源于DIANA模型^[41]用于计算复杂三维场景的辐射区域和二向反射分布函数, 适用于可见光和近红外波段^[42]。热辐射— 图像混合模型(Thermal-Region Radiosity-Graphics combined Model, TRGM)是在热辐射理论和植被冠层发射率方向性的基础上, 将辐射— 图像混合模型扩展到热红外领域^[43]。TRGM能够模拟面元的热辐射和多次散射效应, 因此可用于计算三维场景的方向性亮温。模型主要步骤如下:首先, L— 系统方法被用于生成三维场景; 其次, 计算发射辐射; 然后, 计算多次散射; 最后, 计算方向性辐射或者方向性亮温。Liu等^[43]在北京小汤山对TRGM模型进行了验证。与实测数据比较表明, TRGM模型误差小于2 K。TRGM模型用于模拟植被冠层的方向性亮温, 从而分析植被冠层的热点效应^[44]。TRGM模型考虑了辐射的多次散射效应, 模拟精度较高。由于模型输入参数类型多、数量大以及模拟较大场景时计算量大, 模型应用难度较大。因此该模型特别适合模拟小范围低矮植被冠层, 如小麦、玉米等。

几何投影模型是几何光学模型在热红外遥感中的扩展, 几何光学模型在研究遥感观测方向性方面发挥了极大的作用, 例如, 用几何光学模型研究遥感反演的反射率、植被指数等参数。三维真实结构模型是目前获取异质性下垫面像元尺度LST相对真值的主要途径之一。模型协同与集成, 从而最大限度发挥各个模型的优点, 是未来值得深入研究的方向。几种主要的模型特点归纳如表1所示。

(1) 几何投影模型采用的平行投影方法, 假设在像元尺度内传感器对地面内所有物体的观测方向不变, 这对于卫星遥感是合适的, 但是对于低空或者近地面宽视场角传感器难以表达; 真实结构三维模型可以根据传感器视场角的大小任意调整视场的大小, 适用于所有平台。

(2) DART模型和TRGM模型考虑了树冠内部的多次散射和穿透性; 几何投影模型忽略了树冠内部的多次散射效应。SUM模型的思路也可扩展至自然地表, 但其基本理论也忽略了冠层内部的多次散射。

(3) 几何投影模型以及与之相关的模型只适用于简单自然地表, 如锥形树冠、球形树冠和椭球体树冠等, 虽然通过Ermida等^[16]改进后的模型能适用于更多树冠类型, 但是仍然无法表达复杂地表; 真实结构三维模型可以根据实际需要构建场景模型, 适用于任何地表类型。

(4) 时间复杂度不同。真实结构三维模型需要细分场景, 逐个计算, 所需时间较长, 时间长短与场景大小和细分大小有关, 场景越大、细分面元越小所需时间越长, 可以通过构建空间索引和采用并行计算技术缩短计算时间; 几何投影模型时间复杂度较小。

虽然异质性下垫面像元尺度LST升尺度方法较多, 但是学者主要采用MGP和DART 2种模型用于卫星遥感LST升尺度。由于高分辨传感器获取的LST与地面单点实测值尺度接近, 因而, 目前LST升尺度研究主要集中在中低分辨率传感器道类型的传感器获取LST特点不同。如极轨卫星。不同轨传感器能在连续轨道上以相同的当地太阳时观测地表, 但传感器观测方向在场景中不断变化; 静止轨道卫星传感器以固定的方向持续观测地表, 但每次获取数据时的太阳光照方向不同。

表1

Table 1

表1(Table 1)

表1 各种方法比较 Table 1 Comparison of different methods 方法 模型精度 是否需要构建 三维场景 方法实 现难度 视场类型 时间 复杂度 适用范围 MGP 一般 不需要 一般 平面 较小 简单自然地表 DART 较高 需要 困难 任意 较大 全部地表 SUM 较高 需要 一般 任意 较大 城市地表, 可扩展至自然地表 TRGM 较高 需要 困难 任意 较大 穗期小麦等微尺度结构

表1 各种方法比较 Table 1 Comparison of different methods

表2

Table 2

表2(Table 2)

表2 遥感LST升尺度应用 Table 2 Application of remotely sensed LST upscaling 传感器 轨道 升尺度方法 星下点空间分辨率 时间分辨率 主要研究工作 AVHRR 极轨 MGP 1.1 km 逐日 Pinheiro等[14] MODIS 极轨 MGP/DART 1 km 逐日 Ermida等[16]; Guillevic等[13, 20, 48] VIIRS 极轨 DART 750 m 逐日 Guillevic等[48] SEVIRI 静止 MGP/DART 3 km 15分钟 Ermida等[16]; Guillevic等[13]; Rasmussen等[15]

表2 遥感LST升尺度应用 Table 2 Application of remotely sensed LST upscaling

目前已有较多模型用于异质性下垫面地表温度模拟研究, 能够较好地分析LST的观测方向性特征。然而, 各种模型本身的局限性限制了模型的深入应用。地统计学方法作为一种有效的升尺度方法, 在地表温度以外的其他参数模拟中表现了较好的性能, 该方法对异质性下垫面地表温度升尺度模拟有一定的借鉴意义^{[50, 51]}。在综合分析前人研究的基础上, 作者认为在异质性下垫面像元尺度LST相对真值研究中还需要在以下几个方面开展更加深入的研究。

(1) 地表空间异质性对卫星反演的LST的影响研究

卫星获取的异质性下垫面LST主要受到太阳— 地面— 传感器观测几何的影响和地面三维结构的影响, 目前的异质性LST验证方法中大多考虑了太阳— 地面— 传感器几何关系的影响, 仅有少量研究开始关注像元内地表的空间异质性对LST验证的影响。精确评估地表空间异质性对LST的影响, 从而消除其对模拟相对真值的所产生的误差是准确验证LST的前提。

(2) 构建真实三维场景模拟目标视场

卫星反演的LST与低空大视场角传感器(如四分量净辐射传感器)获取LST进行比较时, 由于四分量视场近似于一个半球空间, 而卫星传感器是沿着某一方向的方向性观测, 视场范围难以匹配, 这必然导致验证出现误差。构建真实三维场景, 以地面实测温度为基础, 实现模型模拟的LST与实测LST的空间范围匹配是异质性LST验证的基础和前提。随着激光雷达技术的发展, 特别是机载激光雷达技术, 精确、快速构建真实三维模型变得更加容易^[52]。

(3) LST尺度转换模型精度与普适性的平衡

现有模型已经能达到很高精度, 如DART模型, 但是由于模型输入参数多, 计算量大, 对少数站点验证可行, 但是对全球大面积进行验证存在较大困难。采用MGP模型随组分温度差异增加, 模型精度显著下降。因此, 有必要找到一种既能满足较高精度需求, 又能快速生成结果的方法。随着计算机并行技术的发展, 将有力推动计算效率提高^[53]。

(4) LST实测数据代表性的问题

目前异质性下垫面像元尺度LST相对真值模拟模型均需要实测组分温度。虽然研究者在很多地方建立了相当多的地面实测站点, 但是在地球表面仍有大面积区域没有或者很少进行卫星温度产品的验证。已有实测站点数据的使用范围值得进一步研究。