青藏地区地应力分布规律研究
[陈志敏1, 2 
, 严松宏2 , 赵德安2, 3 , 余云燕1, 2 ]
, 严松宏引用本文
陈志敏, 严松宏, 赵德安, 余云燕. 青藏地区地应力分布规律研究.地球科学进展, 2015, 30(8): 915-921
Chen Zhimin, Yan Songhong, Zhao Dean, Yu Yunyan. Study on Distribution Rule of Geostress in Qinghai-Tibet Area. Advances in Earth Science, 2015, 30(8): 915-921
Permissions
Chen Zhimin, Yan Songhong, Zhao Dean, Yu Yunyan. Study on Distribution Rule of Geostress in Qinghai-Tibet Area. Advances in Earth Science, 2015, 30(8): 915-921
Copyright©2015, 地球科学进展 编辑部
青藏地区地应力分布规律研究
作者简介：陈志敏(1979-),男,河北临城人,副教授,主要从事高地应力软岩隧道研究. E-mail:chenzhimin0523@126.com
摘要
在中国地应力分布规律统计分析基础上,通过收集200条青藏地区地壳浅层地应力实测结果,首次统计得到我国青藏地区平均水平地应力与垂直地应力的比值随深度变化的分布曲线,并建立了回归方程。进而分析青藏地区地应力分布规律与特点,发现青藏地区地应力具有总体上符合全国地应力规律,其区域地应力受挤压构造作用显著的特点,尤其是岩浆岩中构造应力显著。研究结果对青藏地区地应力的规律性研究具有重要参考价值,对青藏地区地下工程项目勘察设计、结构分析和工程建设具有重要的实用价值。
关键词:
青藏地区; 实测地应力; 回归方程; 构造应力; 分布规律
中图分类号:P642
文献标识码:A
文章编号:1001-8166(2015)08-0915-07
Study on Distribution Rule of Geostress in Qinghai-Tibet Area
Abstract
The distribution curve of the Ratios of the Average Horizontal Geostress and the Vertical Geostresses(RAHVG) varying with depth and regression equation were obtained in Qinghai-Tibet area of China for the first time by collecting and analyzing 200 in-situ measured geostress results based on the analysis of distribution rule of geostress in China. Then the geostress distribution rule and the characteristics were analyzed, and it is found that the geostress in Qinghai-Tibet area conforms to the geostress distribution rule in China, but the geostress in Qinghai-Tibet area is significantly subjected to tectonic squeezing and the tectonic geostress is very obvious in magmatic rock. The RAHVG of the magmatic rock varying with depth in Qinghai-Tibet area is significantly greater than that in China between the depth of 100 m and 800 m. It shows that the stress of the magmatic rock in QinghaiTibet area is significantly subjected to squeezing tectonic. The RAHVG of the sedimentary rock varying with depth in Qinghai-Tibet area is basically consistent with that in China, but the value in Qinghai-Tibet area is greater. It shows that the stress of the sedimentary rock in Qinghai-Tibet area is not significantly subjected to squeezing tectonic. The RAHVG of the metamorphic rock varying with depth in Qinghai-Tibet area is significantly greater than that in China. It shows that the stress of the metamorphic rock in Qinghai-Tibet area is subjected to squeezing tectonic in some degree. This study can provide references to the study of distribution characteristics of geostress in Qinghai-Tibet area. It also has important practical value for underground engineering survey, design, structural analysis and construction in Qinghai-Tibet area.
Keyword:
Qinghai-Tibet area; In-situ measured geostress; Regression equation; Tectonic stress; Distribution rule.
1 引言
地应力是引起开挖工程变形和破坏的根本作用力, 是进行围岩稳定性分析, 实现岩石工程开挖设计和决策科学化的必要前提条件[1]。
地应力分布规律的总结与研究从1912年瑞士地质学家海姆（A．Heim）提出地应力概念并提出静水压力假设开始, 历经1926年苏联学者金尼克（А ．Н ．К И Н Н И К ）对海姆的静水压力假设修正等阶段[2]。随着研究的深入, 人们逐渐认识到地应力的形成与板块边界受压、地幔热对流、地球内应力、地心引力、地球旋转、岩浆侵入和地壳非均匀扩容以及温度不均、水压梯度、地表剥蚀或其他物理化学变化等诸多因素有关。虽然地应力场属于非稳定的应力场, 但相对于工程结构物的设计基准期来说, 可以忽略时间因素, 将其视为相对稳定的应力场进行分析。一般情况下, 主要考虑构造应力场和重力应力场两部分[1], 即使如此, 也很难用函数反映地应力分布规律。自美国垦务局1932 年在哈佛大坝泄水隧道采用表面应力解除法进行了世界首次地应力实测以来, 尤其是我国自20 世纪60 年代首次成功进行原位地应力实测以来, 大量的岩土工程建设取得大量的地应力实测数据, 使得利用统计手段来研究地应力场的分布规律成为可能, 许多学者已做了大量的工作[3]。
Brown等[4]在1978年总结归纳了世界范围内各地区地应力测量结果, 在浅层地壳中平均水平应力普遍大于垂直应力。McCutchen[5]的研究发现浅层水平应力大于垂直应力。
霍克布朗曲线对于世界范围内的地应力分布规律有着指导性意义, 但是由于地应力分布具有很强的区域性, 因而针对不同岩性和特定地区的回归分析曲线对深埋地下结构数值分析中地应力的取值具有重要的参考价值[1]。
Haimson[6]和Zoback[7]等根据水压致裂法测试资料建立了美国的平均水平应力和垂直应力分别随埋深的线性回归关系。Worotniki 和Denham[8]也建立了澳大利亚的平均水平应力和垂直应力随埋深的线性回归关系。
我国区域地应力规律研究结相对滞后, 2007年赵德安等[1]统计分析我国实测地应力随埋深的分布规律, 随后景锋[9]我国大陆浅层地壳实测地应力分布规律研究。由于我国幅员辽阔, 地质条件千差外别, 青藏高原受板块碰撞[10]作用显著隆升[11], 必然形成强烈的高地应力现象, 对深埋地下工程稳定性影响巨大。随着西部开发进程的持续推进, 青藏高原及其边缘地区已经建设或正在建设许多重大工程, 如青藏铁路及其延伸线, 兰武二线、兰渝铁路、兰新二线等。这些大型工程进行了大量的地应力现场实测工作, 为研究青藏地区地应力分布规律提供了必要条件。
2 青藏地区地应力分布规律
2.1 中国地应力分布规律
由于目前收集到的我国青藏地区地应力实测结果大都位于800 m深度以内, 为便于比较分析, 将参考文献[1]中的相关数据取值范围限定在800 m之内。通过回归分析发现分布规律不变, 其平均水平地应力与垂直地应力的比值随深度变化的方程为：
式中：k为平均水平地应力与垂直地应力的比值, H为 深度（m）。
我国三大岩类平均水平地应力与垂直地应力的比值随深度变化的方程为：
岩浆岩：
沉积岩：
变质岩：
2.2 青藏地区实测地应力分析
为了进一步分析我国西部地区, 尤其是青藏地区地应力分布特点, 为工程建设提供参考。本文筛选出我国地应力实测资料中位于青藏地区的地应力实测结果, 测点主要分布于西藏羊八井-康马地区[12]、嘎隆拉隧道[13]、拉日线峡谷区[14]、关角隧道[15]等区域与工程, 由于文献较多恕不一一列举。收集得到岩浆岩数据55条, 沉积岩数据119条, 变质岩数据26条, 共计200条青藏地区地应力实测结果。
依据所收集的青藏地区实测地应力资料, 并剔除个别离散性较大的奇异点, 绘制青藏地区平均水平地应力与垂直地应力比值k与深度关系散点图, 如图1所示。通过回归方法得到比值k值随深度变化规律曲线方程, 即图1中线。通过选取内外边缘实测点, 分别回归得到比值k值随深度变化的内外包线（图1）。其回归方程分别为：
中线：
内包线：
外包线：
将公式(5)和公式(1)绘制曲线, 如图2所示。可以明显看出, 在200 m以内, 青藏地区平均水平地应力与垂直地应力比值中线小于全国中线; 而在200 m~800 m范围内, 青藏地区中线大于全国中线。式中$H$趋于足够大时, 回归公式(1)和(5)分别趋于0.95和1.39, 说明青藏地区地应力受挤压构造作用显著。
3 青藏地区三大岩性地应力分布规律
将所收集到的地应力实测数据按岩浆岩、沉积岩和变质岩三大岩性分别进一步分析, 并与全国的相应岩性随深度分布规律进行比较, 可以更清楚地认识青藏地区的三大岩性的独特地应力分布规律。
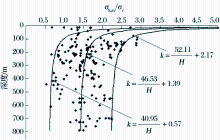 | 图1 青藏地区平均水平地应力与垂直地应力比值及其内外包线随深度变化曲线Fig.1 RAHVG curve and the maximum envelope curve as well as the minimum envelope curve varying with depth in Qinghai-Tibet area |
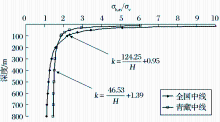 | 图2 青藏平均水平地应力与垂直地应力比值中线与全国中线比较Fig.2 Comparison of RAHVG curves varying with depth in Qinghai-Tibet area and China |
3.1 青藏地区岩浆岩分布规律
将所收集的青藏地区岩浆岩地层的实测地应力资料绘制得到青藏地区平均水平地应力与垂直地应力比值k与深度关系散点图, 如图3所示。通过回归方法得到比值k值随深度变化规律曲线方程, 即图3中线。通过选取内外边缘实测点, 分别回归得到比值k值随深度变化的内外包线（图3）。
青藏地区岩浆岩平均水平地应力与垂直地应力比值及内外包线回归方程分别是：
中线：
内包线：
外包线：
为了进一步分析青藏地区岩浆岩平均水平地应力与垂直地应力比值随深度变化规律, 将其与全国岩浆岩的相应变化规律进行对比, 见图4。
从图4可以看出, 在100 m以内, 青藏地区岩浆岩地层平均水平地应力与垂直地应力比值中线小于全国岩浆岩地层中线; 而在100 m~800 m范围内, 青藏地区岩浆岩地层中线明显大于全国岩浆岩地层中线。比较公式（8）和公式（2）, 当式中H趋于足够大时, k分别趋于1.65和0.7, 说明说明青藏地区岩浆岩中也存在显著的构造应力作用。
3.2 青藏地区沉积岩分布规律
将所收集的青藏地区沉积岩地层的实测地应力资料绘制得到青藏地区平均水平地应力与垂直地应力比值k与深度关系散点图, 如图5所示。通过回归方法得到比值k值随深度变化规律曲线方程, 即图5中线。通过选取内外边缘实测点, 分别回归得到比值k值随深度变化的内外包线（图5）。
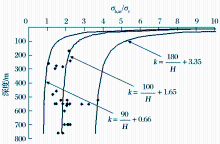 | 图3 青藏地区岩浆岩平均水平地应力与垂直地应力比值及内外包线随深度变化规律Fig.3 RAHVG curve and the maximum envelope curve as well as the minimum envelope curve of the magmatic rock varying with depth in Qinghai-tibet area |
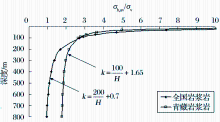 | 图4 青藏地区岩浆岩平均水平地应力与垂直地应力比值中线与全国岩浆岩中线比较Fig.4 Comparison of RAHVG curve of the magmatic rock varying with depth in Qinghai-Tibet area and China |
青藏地区沉积岩平均水平地应力与垂直地应力比值及内外包线回归方程分别是：
中线：
内包线：
外包线：
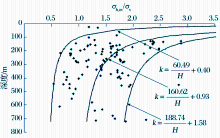 | 图5 青藏地区沉积岩平均水平地应力与垂直地应力比值及内外包线随深度变化规律Fig.5 RAHVG curve and the maximum envelope curve as well as the minimum envelope curve of the sedimentary rock varying with depth in Qinghai-tibet area |
为了进一步分析青藏地区沉积岩平均水平地应力与垂直地应力比值随深度变化规律, 将其与全国沉积岩的相应变化规律进行对比, 见图6。
从图6可以看出, 青藏地区沉积岩地层中线大于全国沉积岩地层中线, 随深度变化规律基本一致。比较公式（11）和公式（3）, 当式中H趋于足够大时, k分别趋于0.93和0.9, 说明青藏地区沉积岩中构造应力作用并不明显。
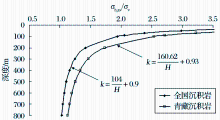 | 图6 青藏地区沉积岩平均水平地应力与垂直地应力比值中线与全国沉积岩中线比较Fig.6 Comparison of RAHVG curve of the sedimentary rock varying with depth in Qinghai-Tibet area and China |
3.3 青藏地区变质岩分布规律
将所收集的青藏地区变质岩地层的实测地应力资料绘制得到青藏地区平均水平地应力与垂直地应力比值k与深度关系散点图, 如图7所示。通过回归方法得到比值k值随深度变化规律曲线方程, 即图7中线。通过选取内外边缘实测点, 分别回归得到比值k值随深度变化的内外包线（图7）。
青藏地区变质岩平均水平地应力与垂直地应力比值及内外包线回归方程分别是：
中线：
内包线：
外包线：
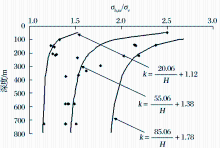 | 图7 青藏地区变质岩平均水平地应力与垂直地应力比值及内外包线随深度变化规律Fig.7 RAHVG curve and the maximum envelope curve as well as the minimum envelope curve of the metamorphic rock varying with depth in Qinghai-Tibet area |
为了进一步分析青藏地区沉积岩平均水平地应力与垂直地应力比值随深度变化规律, 将其与全国沉积岩的相应变化规律进行对比, 见图8。
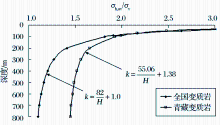 | 图8 青藏地区变质岩平均水平地应力与垂直地应力比值中线与全国变质岩中线比较Fig.6 Comparison of RAHVG curve of the metamorphic rock varying with depth in Qinghai-Tibet area and China |
从图8可以看出, 青藏地区变质岩地层中线总体大于全国变质岩地层中线。在100 m以内, 两条曲线基本重合; 而在100 m~800 m范围内, 青藏地区变质岩地层中线明显大于全国变质岩地层中线。
比较公式（12）和公式（4）, 当式中H趋于足够大时, k分别趋于1.38和1.0, 说明青藏地区变质岩的地层深部有一定的构造应力作用。
3.4 综合分析
由于所收集青藏地区地应力实测资料有限, 使得拟合结果并不十分理想, 但基本体现了该区域的基本特点。
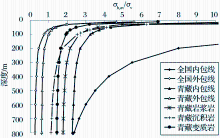
将埋深800 m范围内的我国内外包线和青藏地区内外包线和三大岩类平均水平地应力与垂直地应力比值随深度变化规律分别绘于同一张图上（图9）。
 | 图9 我国内外包线和青藏地区内外包线和三大岩类平均水平地应力与垂直地应力比值随深度变化规律Fig.9 RAHVG curves and the maximum envelope curves as well as the minimum envelope curves of three main kinds of rock in Qinghai-Tibet area and the maximum envelope curve and the minimum envelope curve in China |
从图9可以看出, 在800 m埋深范围内, 青藏地区三大岩类平均水平地应力与垂直地应力比值和内外包线均位于全国整体规律的内外包线以内, 说明青藏地区的地应力结果符合全国总体地应力规律。青藏地区曲线集中在全国整体规律的内外包线内部一定范围, 反映出青藏地区地应力分布呈现独有的特点, 说明研究青藏地区的地应力分布更具实用意义。
对比图9中青藏地区三大岩性曲线, 发现沉积岩和变质岩曲线接近, 而岩浆岩曲线明显位于内侧, 进一步说明青藏地区岩浆岩地层相对于沉积岩和变质岩地层, 明显地保留了较大的构造应力。
4 结论
在中国地应力分布规律统计分析基础上, 通过收集200条青藏地区地壳浅层地应力实测结果, 首次统计得到全国青藏地区平均水平地应力与垂直地应力的比值随深度变化的分布曲线, 并建立了回归方程, 填补了这一地区的研究空白。可得出以下结论：
（1）在200~800 m埋深范围内, 青藏地区平均水平地应力与垂直地应力比值明显大于全国整体水平。当深度足够大时, 青藏地区平均水平地应力与垂直地应力比值最终将趋近于1.39, 明显大于全国整体规律中的0.95。说明青藏地区地应力受挤压构造作用显著。
（2）在100~800 m范围内, 青藏地区岩浆岩地层中线明显大于全国岩浆岩地层中线。当深度足够大时, 青藏地区岩浆岩地层平均水平地应力与垂直地应力比值最终将趋近于1.65, 明显大于全国岩浆岩地层规律中的0.7。说明青藏地区地应力受挤压构造作用显著。
（3）青藏地区沉积岩地层中线大于全国沉积岩地层中线, 随深度变化规律基本一致。当深度足够大时, 青藏地区和全国沉积岩地层平均水平地应力与垂直地应力比值分别趋于0.93和0.9, 说明青藏地区沉积岩中构造应力作用并不明显。
（4）青藏地区变质岩地层中线总体大于全国变质岩地层中线, 特别是在100~800 m范围内。当深度足够大时, 青藏地区和全国沉积岩地层平均水平地应力与垂直地应力比值分别趋于1.38和1.0, 说明青藏地区变质岩的地层深部有一定的构造应力作用。
（5）青藏地区三大岩类平均水平地应力与垂直地应力比值和内外包线均位于全国整体规律的内外包线以内, 说明青藏地区的地应力结果符合全国总体地应力规律。青藏地区曲线集中在全国整体规律的内外包线内部一定范围, 反映出青藏地区地应力分布呈现独有的特点, 说明研究青藏地区的地应力分布更具实用意义。
（6）对比图9中青藏地区三大岩性曲线, 发现沉积岩和变质岩曲线接近, 而岩浆岩曲线明显位于内侧, 进一步说明青藏地区岩浆岩地层相对于沉积岩和变质岩地层, 明显地保留了较大的构造应力。
The authors have declared that no competing interests exist.
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|