地壳结构对GRACE估算中国大陆地表垂直负荷形变的影响<sup>*</sup>

引用本文

贾路路, 相龙伟, 汪汉胜. 地壳结构对GRACE估算中国大陆地表垂直负荷形变的影响^* . 地球科学进展, 2014, 29(7): 828-834
Jia Lulu, Xiang Longwei, Wang Hansheng. Effects of Crustal Structure for Estimation of Vertical Load Deformation on the Solid Earth Using GRACE in China Mainland. Advances in Earth Science, 2014, 29(7): 828-834 复制到剪切板

Permissions

This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

地壳结构对GRACE估算中国大陆地表垂直负荷形变的影响^*

贾路路^1,², 相龙伟^2,³, 汪汉胜²

1. 地壳运动监测工程研究中心, 北京 100036

2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北武汉 430077

3. 中国科学院大学, 北京 100049

作者简介：贾路路(1984-),男,山东德州人,助理研究员,主要从事时变重力场信号处理和地球物理解释的研究．E-mail:lljia@neis.gov.cn

基金:国家自然科学基金项目“联合GRACE和卫星测高分离南极GIA和冰质量平衡的研究”(编号：41204013);

地壳工程中心主任基金项目(2013)“联合卫星重力和GPS研究中国大陆地表质量驱动的周年垂直形变”资助

摘要

根据重力卫星GRACE(Gravity Recovery and Climate Experiment)估算固体地表垂直负荷形变时通常采用的PREM (Preliminary Reference Earth Model) 地球模型不能较好地反映中国大陆特别是青藏高原巨厚的地壳结构。基于考虑中国大陆区域地壳结构的地球模型计算了新的负荷勒夫数,探讨了地壳结构差异对GRACE卫星RL05观测数据估算中国大陆地表垂直负荷形变的影响。结果表明,区域地壳结构差异对GRACE估算中国大陆地表负荷形变的影响较为明显,90阶垂直位移负荷勒夫数的相对差异接近11%;前90阶垂直负荷形变差异的极值出现在青藏高原东南部,最大相对差异达到10%左右,均方根相对差异为4%。建议利用GRACE卫星RL05数据估算中国大陆地表垂直负荷形变时,应该使用更加趋于真实的区域地壳结构替代PREM模型的相应部分。

关键词: 卫星重力; 地表质量负荷; 垂直形变; 区域地壳结构; 中国大陆

中图分类号:P312.1 文献标志码:A 文章编号:1001-8166(2014)07-0828-07

Effects of Crustal Structure for Estimation of Vertical Load Deformation on the Solid Earth Using GRACE in China Mainland

Jia Lulu^1,², Xiang Longwei^2,³, Wang Hansheng²

1. National Earthquake Infrastructure Service, Beijing 100036, China

2. State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China

3. University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

When the inversion of vertical load deformation on Earth’s surface using GRACE (Gravity Recovery and Climate Experiment) data, the load Love numbers based on PREM (Preliminary Reference Earth Model) are commonly used. But the crustal structure under China mainland especially under Tibet Plateau is quite different from that given by PREM Earth model. New load Love numbers were calculated based on a modified Earth model which accounted for regional crustal structure in China mainland. And the effect of regional crustal structure in China mainland for estimation of vertical load deformation on Earth’s surface using GRACE RL05 data was investigated in this paper. It is found that the effect of crustal difference is very prominent. The relative difference of load Love numbers for vertical deformation can reach about 11% at degree 90. The extreme value of difference in vertical load deformation below 90 degree of spherical harmonic coefficients located at the southeastern Tibet Plateau and the maximum relative difference reaches 10%. The relative difference of the root mean square is about 4%. It is suggesting that an Earth model with a more realistic crustal structue instead of PREM should be used for the estimation of vertical load deformation in China mainland espacially in Tibet Plateau.

Keyword: Satellite gravity; Solid Earth mass loading; Vertical deformation; Regional crustal structure; China mainland.

Show Figures

1 引言

研究地表质量变化驱动的垂直形变及其变化可了解大气、海洋和陆地水等地表质量运动和相互作用等信息,对全球气候变化和地球动力学研究具有重要的意义。地表质量负荷变化不仅会引起地球重力场的变化,还会引起固体地球的垂直形变。这种弹性形变特别是陆地水储量的变化（含冰雪）所引起的周年地表垂直形变可达数厘米^{[ 1]},能够被地面观测(GPS等技术)相应地监测到^{[ 2, 3]}。

重力卫星GRACE(Gravity Recovery and Climate Experiment)^{[ 4, 5]}自发射以来已对全球重力场变化进行了十余年的连续观测。由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^{[ 6, 7]}、极地冰盖质量变化^{[ 8, 9, 10]}等方面的研究。而根据弹性负荷理论^{[ 11]},由GRACE时变重力数据不仅能够得到地表质量负荷变化引起的重力场变化,也能够估算地表负荷变化所引起的地表垂直形变^{[ 12]}。

在目前利用重力卫星GRACE估算地表垂直负荷形变的计算中^{[ 13, 14, 15]},一般采用基于PREM（Preliminary Reference Earth Model）地球模型^{[ 16]}得到的负荷勒夫数^{[ 11, 17]}, 但该模型使用的是全球平均的弹性结构参数（密度、P波速度、S波速度等）,不能很好地反映中国大陆特别是青藏高原巨厚的地壳结构。而根据Wang等^{[ 18]}利用水文模拟数据的研究,区域地壳结构对GPS估算地表质量负荷的影响不容忽视。

为了研究区域地壳弹性结构的差异对GRACE观测数据估算中国大陆地表垂直负荷形变的影响,本文首先基于考虑中国大陆地壳结构的M-PREM模型计算得到了新的负荷勒夫数,然后将该负荷勒夫数用于GRACE卫星RL05数据估算中国大陆地表垂直负荷形变,用来与PREM模型相应的结果做对比分析。

2 地球模型和负荷勒夫数

在计算负荷勒夫数时所使用的地球模型通常为PREM模型,其弹性结构参数是全球平均的结果。然而,中国大陆尤其是青藏高原地区具有世界上最厚的地壳结构,PREM模型及由此模型计算的负荷勒夫数不能较好的反应该地区的特性。

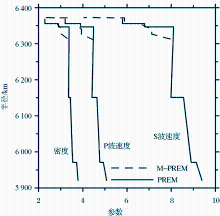
Laske等^{[ 19]}发展的Crust2.0地壳模型给出的地壳弹性结构在深度方向有更高的分辨率、更加接近于真实,该模型与PREM的全球平均地壳结构有着明显的差异。为了探讨地壳结构差异对GRACE估算中国大陆地壳垂直负荷形变的影响,我们基于PREM模型和Crust2.0地壳模型构造了改进的地球模型：M-PREM,该模型在地壳以下使用了PREM给出的物理参数,而地壳弹性结构则使用了Crust2.0在中国大陆的参数平均值替代PREM模型的相应部分,具体参数差异如图1所示。这样我们就在PREM模型的基础上对中国大陆地壳结构进行了精化,特别是对浅层地壳部分做了细分,所得改进的地球模型M-PREM能够更好的反映中国大陆区域地壳结构,而不是全球范围内的平均;进而根据M-PERM模型研究中国大陆地壳垂直负荷形变也更为合理,所得结果更能反映中国区域的实际值。然后分别基于M-PREM和PREM 2个地壳结构不同的地球模型,我们计算了负荷勒夫数 h _l和 k _l,具体方法可参见相关文献^{[ 20]},其中 h _l是与垂直位移有关的负荷勒夫数,而 k _l是和重力变化有关的负荷勒夫数。

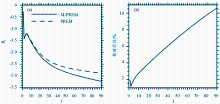
	Figure Option View Download New Window
	图1 M-PREM和PREM地球模型参数差异Fig.1 The difference of parameters from M-PREM and PREM

由于现阶段GRACE重力卫星RL05数据的最高阶数为90,所以本文关注的是地壳结构差异对前90阶垂直负荷勒夫数的影响。图2显示了基于上述不同地球模型所得到的垂直负荷勒夫数 h _l及其相对差异。图2a中,实线表示的是基于M-PREM模型的垂直负荷勒夫数,而虚线表示基于PREM模型的相应结果。可以看到基于M-PREM的 h _l值在前90阶都要比PREM的结果大。这是由于M-PREM模型中地壳结构的密度、P波速度以及S波速度都要比PREM模型的小一些,进而M-PREM模型相应的弹性Lame常数也比PREM模型的要小^{[ 18]}。

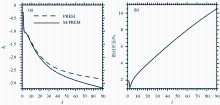	Figure Option View Download New Window
	图2 （a）基于M-PREM和PREM地球模型的负荷勒夫数及（b）相对差异Fig.2 (a) Values of load Love numbers based on M-PREM and PREM earth model and (b) the relative difference

图2b显示了基于上述两个不同地球模型所得的垂直负荷勒夫数 h _l的相对差异。由图2b可知,垂直负荷勒夫数的相对差异在前90阶呈现上升趋势,阶数越高相对差异越大;60阶的相对差异约为8%,而90阶的差异则非常接近11%。这可能会对GRACE估算中国大陆地表垂直负荷形变产生较大的影响。

3 GRACE数据及估算地表垂直负荷形变

本文使用德国地学中心（German Research Centre for Geosciences,GFZ）发布的GRACE卫星2003年1月至2012年12月时段10年共115个月（缺失5个月）的RL05数据,其球谐截断阶数为90阶,该数据主要反映了陆地水变化的信号。虽然RL05数据较之前的RL04数据在空间分辨率和精度上都有所提高,“条带”误差明显减小^{[ 21]},但还需要数据后处理来提高信噪比以满足研究需要。首先将每月重力场系数扣除观测时段的均值,然后采用Chambers提出的P3M10方法^{[ 22]}对扣除均值的GRACE重力场系数进行去相关处理,最后利用对真实信号影响较小^{[ 23]}的高斯滤波^{[ 24]}对去相关后的系数进行空间平滑,用以压制重力卫星观测数据的高阶误差。

根据GRACE观测的时变重力场球谐系数,可由以下公式计算地表质量驱动的垂直负荷形变^{[ 1]},具体推导过程可参见相关文献^{[ 25]}：

(1)

式中： a为地球平均半径; 为余纬和经度; l,m为球谐系数的阶次,最高阶数 lmax=90; W _l为高斯滤波系数,鉴于RL05数据质量的提高,本文采用了较小的滤波半径150km; 为扣除均值之后的月重力场系数; 为正则化勒让德函数; h _l和 k _l为负荷勒夫数。

根据公式（1）,分别采用基于考虑中国大陆地壳结构的M-PREM模型以及PREM模型所得不同的负荷勒夫数估算垂直负荷形变,其差异就反映了地壳结构差异对GRACE估算中国大陆地表垂直负荷形变的影响。这里定义 ,地壳结构差异对估算垂直负荷形变的影响通过该因子直接反映出来。图3显示了基于M-PREM模型和PREM模型所得因子 B _l的值以及它们的相对差异。由图3a可知,基于M-PREM模型得到的 B _l值在前90阶要比PREM模型所得的结果大,这说明考虑中国大陆地壳结构的M-PREM模型更易产生垂直负荷形变;与垂直负荷勒夫数的 h _l差异相一致,2个模型所得 B _l值的相对差异也随着阶数的增长而增大,90阶的相对差异已约达到11%。

	Figure Option View Download New Window
	图3 （a）基于M-PREM和PREM地球模型的因子 B _l值及（b）相对差异Fig.3 (a) Values of B _l based on M-PREM and PREM Earth model and (b) the relative difference

4 结果与分析

根据公式（1）计算了中国大陆1°×1°垂直负荷形变时间序列,扣除周年变化、半年变化以及161天变化等周期项后,就可得到GRACE估算的前90阶的垂直负荷形变线性速率分布。

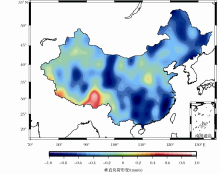
图4显示了基于M-PREM模型GRACE估算的中国大陆垂直负荷形变线性速率。根据弹性负荷理论,图4中的垂直负荷形变速率正值表示在观测时段（2003—2012年）地表质量呈减少趋势,而负值则表示地表质量呈增加趋势。GRACE观测的中国大陆地表负荷形变的线性速率,主要反映了气候驱动和人为因素影响下的地表质量的分布状态。GRACE垂直负荷形变速率大小分布因地而异,总体来说,中国北方的垂直速率一般较小,而南方垂直速率较大,最大的正速率位于雅鲁藏布江-澜沧江流域,大约达到0.95mm/a,很大程度上反映了中国大陆南北方的气候差异。除了降水等自然因素的影响^{[ 26]},人为因素也会对地表质量分布产生很大的影响,从而造成地表垂直负荷形变速率的变化。例如华北地区地下水抽取、煤矿开采等因素都会造成该地区地表质量流失^{[ 27, 28]},在图4中表现为明显的垂直形变正速率;而三峡水库的蓄水^{[ 6, 29]}则造成该地区垂直负荷形变负异常。

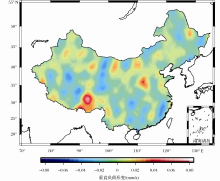
	Figure Option View Download New Window
	图4 基于M-PREM模型的垂直负荷形变线性趋势Fig.4 Linear trend of vertical load deformation based on M-PREM

如前所述,为了探讨区域地壳结构对GRACE估算中国大陆地表垂直负荷形变的影响,本文也采用PREM模型的负荷勒夫数计算了研究区的垂直负荷形变速率;比较M-PREM模型结果和PREM模型结果的差异,就可以分析地壳结构差异对估算结果的影响。

对于基于PREM模型估算的垂直负荷形变速率,限于篇幅本文不再图示。我们直接给出了基于2种不同地壳结构模型估算垂直负荷形变的差异。通过图5可以看到,2种模型估算结果的差异较大,最大差异位于青藏高原东南部的雅鲁藏布江流域,幅值约达到0.09mm/a,这对于估算的结果（图4所示,幅值约为0.95mm/a）而言是非常明显的,最大相对差异接近10%;而根据Wahr等^{[ 30]}的类似评估方法,我们估算了GRACE监测中国大陆地表垂直负荷形变速率的误差,其最大值约为0.06mm/a,该值要小于2个模型所得结果差异的最大值;地壳结构产生的差异和图4所示的估算结果有明显的相关性,M-PERM模型估算结果的幅值要比PREM模型的大,说明考虑中国大陆区域地壳结构的M-PREM模型较全球平均的PREM模型更易产生垂直负荷形变;为了定量描述差异的大小,本文统计了M-PREM模型和PREM模型估算结果的均方根,分别为0.52mm/a和0.50mm/a,可以得到两个模型前90阶的估算结果在中国大陆的相对差异达到4%。

	Figure Option View Download New Window
	图5 不同地壳结构估算垂直负荷形变的差异Fig.5 Difference of inversion of vertical load deformation based on different crustal structure

5 结论

本文利用GRACE卫星RL05的90阶数据探讨中国大陆区域地壳结构差异对估算地表垂直负荷形变的影响。通过比较不同地壳模型的负荷勒夫数可知, M-PREM模型的负荷勒夫数比PREM模型的要大,随着阶数的增大差异越来越大,90阶的相对差异达到11%左右;而对于GRACE估算的地表垂直负荷形变速率,2种模型前90阶结果差异的幅值达到约0.09mm/a,最大相对差异约为10%;2种模型估算结果的均方根的相对差异达到4%。研究表明,在使用GRACE重力卫星RL05的90阶数据估算中国大陆地表垂直负荷形变时,区域地壳结构的影响不容忽视,特别是对将来具有更高精度和分辨率的重力卫星,建议使用类似M-PREM等地壳结构更加趋于真实的地球模型进行估算。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Davis J, Elósegui P, Mitrovica J, et al. Climate-driven deformation of the solid Earth from GRACE and GPS[J]. Geophysical Research Letters, 2004, 31(24): L24605, doi: DOI:10.1029/2004GL021435. [本文引用:2] [JCR: 3.982]
[2]	Wahr J, Dam T, Larson K, et al. Geodetic measurements in Greenland and their implications[J]. Journal of Geophysical Research, 2001, 106(B8): 16567-16581. [本文引用:1]
[3]	Nielsen K, Khan S A, Spada G, et al. Vertical and horizontal surface displacements near Jakobshavn Isbrea driven by melt-induced and dynamic ice loss[J]. Journal of Geophysical Research, 2013, 118(4): 1837-1844. [本文引用:1]
[4]	Tapley B D, Bettadpur S, Ries J C, et al. GRACE measurements of mass variability in the Earth system[J]. Science, 2004, 305(5683): 503-505. [本文引用:1]
[5]	Tapley B D, Bettadpur S, Watkins M, et al. The gravity recovery and climate experiment: Mission overview and early results[J]. Geophysical Research Letters, 2004, 31(9): L09607, doi: DOI:10.1029/2004GL019920. [本文引用:1] [JCR: 3.982]
[6]	Wang Hansheng, Wang Zhiyong, Yuan Xudong. Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data[J]. Chinese Journal of Geophysics, 2007, 50(3): 730-736. [汪汉胜, 王志勇, 袁旭东. 基于GRACE 时变重力场的三峡水库补给水系水储量变化[J]. 地球物理学报, 2007, 50(3): 730-736. ] [本文引用:2]
[7]	Wahr J, Swenson S, Zlotnicki V, et al. Time-variable gravity from GRACE: First results[J]. Geophysical Research Letters, 2004, 31(11): L11501, doi: DOI:10.1029/2004GL019779. [本文引用:1] [JCR: 3.982]
[8]	Jia Lulu, Wang Hansheng, Xiang Longwei, et al. Effects of glacial isostatic adjustment on the estimation of ice mass balance over Antarctica and the uncertainties[J]. Chinese Journal Geophysics, 2011, 54(6): 1466-1477. [贾路路, 汪汉胜, 相龙伟, 等. 冰川均衡调整对南极冰质量平衡监测的影响及其不确定性[J]. 地球物理学报, 2011, 54(6): 1 466-1 477. ] [本文引用:1] [CJCR: 0.5277]
[9]	King M A, Bingham R J, Moore P, et al. Lower satellite-gravimetry estimates of Antarctic sea-level contribution[J]. Nature, 2012, 491(7425): 586-589. [本文引用:1] [JCR: 38.597]
[10]	Ivins E R, James T S, Wahr J, et al. Antarctic contribution to sea level rise observed by GRACE with improved GIA correction[J]. Journal of Geophysical Research, 2013, 118(6): 3126-3141.  [本文引用:1]
[11]	Farrell W. Deformation of the Earth by surface loads[J]. Reviews of Geophysics and Space Physics, 1972, 10(3): 761-797. [本文引用:2]
[12]	Liao Haihua, Zhong Min, Zhou Xuhua. Climate-driven annual vertical deformation of solid Earth calculated from GRACE[J]. Chinese Journal of Geophysics, 2010, 53(5): 1091-1098. [廖海华, 钟敏, 周旭华. 利用 GRACE 卫星重力资料解算气候驱动的地表周年垂直形变[J]. 地球物理学报, 2010, 53(5): 1091-1098. ] [本文引用:1]
[13]	Fu Y, Freymueller J T. Seasonal and long-term vertical deformation in the Nepal Himalaya constrained by GPS and GRACE measurements[J]. Journal of Geophysical Research, 2012, 117(B3): B03407, doi: DOI:10.1029/2011JB008925. [本文引用:1]
[14]	Kusche J, Schrama E. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data[J]. Journal of Geophysical Research, 2005, 110(B9): B09409, doi: DOI:10.1029/2004JB003556. [本文引用:1]
[15]	Zhang Liangjing, Jin Shuanggen, Zhang Tengyu. Seasonal variations of Earth’s surface deformation estimated from GPS and satellite gravimetry[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 32-38. [张良镜, 金双根, 张腾宇. 用GPS和卫星重力观测估计地表形变的季节性变化[J]. 大地测量与地球动力学, 2012, 32(2): 32-38. ] [本文引用:1] [CJCR: 1.292]
[16]	Dziewonski A M,  Anderson D L. Preliminary reference Earth model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356. [本文引用:1] [JCR: 2.383]
[17]	Wang Hansheng, Xu Houze, Li Guoying. Improvement of computation of load Love numbers of SNREI Earth model[J]. Chinese Journal Geophysics, 1996, 39(Suppl. ): 182-189. [汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷勒夫数数值计算的新进展[J]. 地球物理学报, 1996, 39(增刊): 182-189. ] [本文引用:1] [CJCR: 0.5277]
[18]	Wang H, Xiang L, Wu P, et al. Effects of the Tibetan Plateau crustal structure on the inversion of water trend rates using simulated GRACE/GPS data[J]. Terrestrial, Atmospheric & Oceanic Sciences, 2013, 24(4): 505-512. [本文引用:2]
[19]	Laske G, Masters G, Reif C. CRUST 2. 0: A New Global Crustal Model at 2×2 Degrees[DB/OL]. 2011[2014-02-17]. http:∥igppweb.ucsd.edu/~gabi/crust2.html. [本文引用:1]
[20]	Wang H, Xiang L, Jia L, et al. Load love numbers and Green’s functions for elastic Earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2. 0[J]. Computer & Geoscience, 2012, 49: 190-199. [本文引用:1] [JCR: 1.675]
[21]	Ju Xiaolei, Shen Yunzhong, Zhang Zizhan. Antarctica ice mass change analysis based on GRACE RL05 data[J]. Chinese Journal of Geophysics, 2013, 56(9): 2918-2927. [鞠晓蕾, 沈云中, 张子占. 基于GRACE卫星RL05数据的南极冰盖质量变化分析[J]. 地球物理学报, 2013, 56(9): 2918-2927. ] [本文引用:1]
[22]	Chambers D P. Observing seasonal steric sea level variations with GRACE and satellite altimetry[J]. Journal of Geophysical Research, 2006, 111(C3): C03010, doi: DOI:10.1029/2005JC002914. [本文引用:1]
[23]	Steffen H, Wu P, Wang H. Determination of the Earth’s structure in Fennoscand ia from GRACE and implications on the optimal post-processing of GRACE data[J]. Geophysical Journal International, 2010, 182(3): 1295-1310. [本文引用:1] [JCR: 2.853]
[24]	Wahr J, Molenaar M. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30205-30229. [本文引用:1]
[25]	Jia Lulu. Effects of Glacial Isostatic Adjustment on the Estimate of Present-Day Mass Balance on the Earth’s Surface[D]. Beijing: University of Chinese Academy of Sciences, 2012. [贾路路. 冰川均衡调整对现今地表质量平衡监测影响的研究[D]. 北京: 中国科学院大学, 2012. ] [本文引用:1]
[26]	Liu Yang, Wei Zhigang. Comparison of the precipitation cycle and trend in different areas of Northern China in recent 50 years[J]. Advances in Earth Science, 2012, 27(3): 337-346. [刘扬, 韦志刚. 近50年中国北方不同地区降水周期趋势的比较分析[J]. 地球科学进展, 2012, 27(3): 337-346. ] [本文引用:1] [CJCR: 1.388]
[27]	Tang Q, Zhang X, Tang Y. Anthropogenic impacts on mass change in North China[J]. Geophysical Research Letters, 2013, 40(15): 3924-3928. [本文引用:1] [JCR: 3.982]
[28]	Meng Suhua, Fei Yuhong, Zhang Zhaoji, et al. Research on spatial and temporal distribution of the precipitation infiltration amount over the past 50 years in North China Plain[J]. Advances in Earth Science, 2013, 28(8): 923-929. [孟素花, 费宇红, 张兆吉, 等. 50年来华北平原降水入渗补给量时空分布特征研究[J]. 地球科学进展, 2013, 28(8): 923-929. ] [本文引用:1] [CJCR: 1.388]
[29]	Wang X, De Linage C, Famiglietti J, et al. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in situ measurements[J]. Water Resources Research, 2011, 47(12): W12502, doi: DOI:10.1029/2011WR010534. [本文引用:1] [JCR: 3.149]
[30]	Wahr J, Swenson S, Velicogna I. Accuracy of GRACE mass estimates[J]. Geophysical Research Letters, 2006, 33(6): L06401, doi: DOI:10.1029/2005GL025305. [本文引用:1] [JCR: 3.982]

2004

3.982

0.0

. 2004, 31(24):null-null

Climate-driven deformation of the solid Earth from GRACE and GPS

J. L. Davis 1 ,P. Elósegui 1,3 ,J. X. Mitrovica 2 andM. E. Tamisiea 1

1 Harvard-Smithsonian Center for Astrophysics, Cambridge, Massachusetts, USA 2 Department of Physics, University of Toronto, Ontario, Canada 3 Also at Institut Estudis Espacials de Catalunya, Consejo Superior de Investigaciones Científicas, Barcelona, Spain.

> [1] GRACE data indicate large seasonal variations in gravity that are assumed to be related to climate-driven fluxes of surface water. Seasonal redistribution of surface mass should deform the Earth, and our calculations using GRACE data suggest vertical deformations of ∼13 mm in the region of greatest flux, the Amazon River Basin. To test the GRACE gravity-hydrology connection, we analyzed GPS data acquired from sites in this region. After accounting for degree 1 variations not observable with GRACE, we find that annual deformation measured with GPS correlates highly with predictions calculated from GRACE measurements. These results confirm the variations in surface water sensed by GRACE, which are significantly larger than those predicted by some hydrology models. The results also demonstrate that GRACE can be an important tool for monitoring deformation of the Earth, and suggest that combined analysis of GRACE and GPS may be a useful approach for estimation of geocenter variations.

... 这种弹性形变特别是陆地水储量的变化（含冰雪）所引起的周年地表垂直形变可达数厘米^[1],能够被地面观测(GPS等技术)相应地监测到^[2,3] ...

... 根据GRACE观测的时变重力场球谐系数,可由以下公式计算地表质量驱动的垂直负荷形变^[1],具体推导过程可参见相关文献^[25]： ...

2001

0.0

. 2001, 106(B8):16567-16581

Geodetic measurements in Greenland and their implications

John WahrTonie van DamKristine LarsonOlivier Francis

> We describe results from an ongoing experiment in Greenland, in which we are using absolute gravity and continuous Global Positioning System (GPS) measurements to study vertical crustal motion at two locations along the edge of the ice sheet: Kellyville, located about one third of the way up the western ice margin, and Kulusuk, located along the eastern ice margin at about the same latitude as Kellyville. The GPS measurements suggest average crustal uplift rates of −5.8±1.0 mm/yr at Kellyville and −2.1±1.5 mm/yr at Kulusuk. There have not yet been enough absolute gravity occupations to permit useful secular gravity solutions at either location. The negative uplift rate at Kellyville is consistent with independent archeological and historical evidence that the southwestern edge of the continent has been subsiding over the last 3000 years, but it is inconsistent with estimates of the Earth's continuing viscoelastic response to melting ice during the early Holocene, which predict that Kellyville is likely to be uplifting, rather than subsiding, by 2.0±3.5 mm/yr. The resulting −7.8±3.6 mm/yr discrepancy between the observed and predicted uplift rates is too large to be caused by loading from present-day changes in nearby ice. However, it is consistent with independent suggestions that the western ice sheet margin in this region may have advanced by ≈50 km during the past 3000–4000 years. If this advance did occur and if the crustal subsidence it induces is not removed from altimeter measurements of Greenland ice sheet elevations, then the altimeter solutions could underestimate the true snow/ice thickness change by 5–10 mm/yr along portions of the western margin of the ice sheet.

... 这种弹性形变特别是陆地水储量的变化（含冰雪）所引起的周年地表垂直形变可达数厘米^[1],能够被地面观测(GPS等技术)相应地监测到^[2,3] ...

2013

0.0

... 这种弹性形变特别是陆地水储量的变化（含冰雪）所引起的周年地表垂直形变可达数厘米^[1],能够被地面观测(GPS等技术)相应地监测到^[2,3] ...

2004

0.0

Science. 2004, 305(5683):503-505

GRACE Measurements of Mass Variability in the Earth System

Byron D. Tapley 1 , Srinivas Bettadpur 1 , John C. Ries 1 , * , Paul F. Thompson 1 , Michael M. Watkins 2

1 Center for Space Research, University of Texas, Austin, TX 78712, USA. 2 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91125, USA. ↵ * To whom correspondence should be addressed. E-mail: ries@csr.utexas.edu

... 重力卫星GRACE(Gravity Recovery and Climate Experiment)^[4,5]自发射以来已对全球重力场变化进行了十余年的连续观测 ...

2004

3.982

0.0

... 重力卫星GRACE(Gravity Recovery and Climate Experiment)^[4,5]自发射以来已对全球重力场变化进行了十余年的连续观测 ...

2007

0.0

. 2007, 50(3):730-736

Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data

1 Key Laboratory of Dynamic Geodesy, Institute of Geodesy & Geophysics, Chinese Academy of Sciences, Wuhan 430077, China 2 Graduate University of Chinese Academy of Sciences, Beijing 100049, China 3 Department of Geology & Geophysics, University of Calgary, Calgary T2N 1N4, Canada 4 Department of Geomatics Engineering, University of Calgary, Calgary T2N 1N4, Canada

Twentytwo monthly water storage changes are predicted for the supply water systems of the Three Gorges Reservoir from GRACE timevariable gravity data. In order to assess the results, the CPC hydrological models are used to establish two benchmarks. It is found that the results are very reasonable in this area. For Gaussian averaging radius of 1000 km, the total water storage changes in the area have a peaktopeak value of 14 cm, and the annual component has an amplitude of 58 cm and a phase of -408 days. The RMS difference compared with the inversion results with the same averaging radius using the synthetic gravity data from the CPC models is 13 cm for the total water storage changes, and the differences are 01 cm and 10 day for the amplitude and phase of the annual component. However, for checking the ability of GRACE to monitor the true water storage changes within the area, it is also very necessary to compare the inversion results from GRACE gravity models with the true average results of CPC models. For this comparison the RMS difference is 21 cm for the total water storage changes, and the differences are 17 cm and 93 days for the amplitude and phase of the annual component. Comparing the assessment results of the two comparisons, it is found that the first comparison has overestimated the effectiveness of GRACE. Nevertheless, the second comparison shows that the monthly water storage changes can be roughly determined from GRACE data in this area.

利用22个月的GRACE时变重力场，反演了三峡水库补给水系的水储量变化，并按月给出了数值结果.与水文学同化模型（CPC）的两组比较说明基于GRACE重力的反演结果是合理的.当高斯平均半径为1000 km时，该区总水储量变化的峰谷差为14 cm，其年变化振幅为58 cm，相位为-408天，与CPC模型合成重力数据的反演结果进行比较，其总水储量变化均方差为13 cm，年变化振幅相差01 cm，相位相差10天.为进一步检验GRACE能否监测该区真实水储量变化，还将其反演结果与CPC模型的真实平均结果进行比较，结果发现总体均方差为21 cm，年变化振幅相差17 cm，相位相差93天.因此，第一种比较过高地估计了GRACE监测该区水储量变化的能力，第二种比较则较真实地反映了实际情况，尽管反演结果与水文学的结果差别较大，但仍然显示GRACE能监测该区每月的水储量变化.

... 由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^[6,7]、极地冰盖质量变化^[8,9,10]等方面的研究 ...

... 而三峡水库的蓄水^[6,29]则造成该地区垂直负荷形变负异常 ...

2004

3.982

0.0

. 2004, 31(11):null-null

Time-variable gravity from GRACE: First results

John Wahr 1 ,Sean Swenson 1 ,Victor Zlotnicki 2 andIsabella Velicogna 1

1 Department of Physics and CIRES, University of Colorado, Boulder, Colorado, USA 2 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California, USA

> [1] Eleven monthly GRACE gravity field solutions are now available for analyses. We show those fields can be used to recover monthly changes in water storage, both on land and in the ocean, to accuracies of 1.5 cm of water thickness when smoothed over 1000 km. The amplitude of the annually varying signal can be determined to 1.0 cm. Results are 30% better for a 1500 km smoothing radius, and 40% worse for a 750 km radius. We estimate the annually varying component of water storage for three large drainage basins (the Mississippi, the Amazon, and a region draining into the Bay of Bengal), to accuracies of 1.0–1.5 cm.

... 由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^[6,7]、极地冰盖质量变化^[8,9,10]等方面的研究 ...

2011

0.0

0.5277

. 2011, 54(6):1466-1477 DOI:10.3969/j.issn.0001-5733.2011.06.006

Effects of glacial isostatic adjustment on the estimation of ice mass balance over Antarctica and the uncertainties

1. Key Laboratory of Dynamical Geodesy, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China; 2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China; 3. Department of Geoscience, University of Calgary, Calgary T2N 1N4, Canada; 4. Chinese Antarctic Center of Surveying and Mapping, Wuhan 430079, China

The effects of glacial isostatic adjustment (GIA) on monitoring ice mass balance over Antarctica are investigated using our newly-released GIA model ICE-4G+RF3L20( β =0.4) and the uncertainties are evaluated by considering the effects of differences in ice load models and reference mantle viscosities. The results and the comparison with those from GRACE time-varying gravity fields and satellite altimetry data are shown as follows. It is found that the GIA has strong effects on monitoring the changes of equivalent water height (EWH) from GRACE gravity data, significant GIA effects occur at Ross Ice Shelf, Kamb Ice Stream, Ronne Ice Shelf and Antarctic Peninsula with a maximal magnitude of ~29.8 mm/a at Kamb Ice Stream. For the whole Antarctica, the effect of GIA on total ice mass balance is 134±28 Gt/a. The differences in ice models account for 88.4% of the variances of uncertainties while the differences in viscosity models contribute 11.6%. In some typical regions, the changes of EWH monitored by GRACE data are given before and after GIA corrections. These are ~32.8 mm/a and ~6.3 mm/a for Kamb Ice Stream, ~-95.3 mm/a and ~-102.5 mm/a for Amundsen Sea Embayment, ~13.6 mm/a and ~8.1 mm/a for Enderby Land. The total ice mass change of the whole Antarctica is found to be -82±29 Gt/a after GIA corrections which is quite close to that estimated from satellite altimetry data. Furthermore, the effects of GIA on the ice height changes observed from ICESat are less than 8%. The results related to our new GIA model in this paper can be utilized to precisely monitor the present ice mass balance in Antarctica from space geodetic techniques.

本文研究了新的全球冰川均衡调整(GIA)模型对南极冰盖质量平衡监测的影响,考虑现有冰川负荷模型和地幔黏滞度模型的差异,完整评估了结果的不确定性,最后结合GRACE和卫星测高的结果进行了对比分析.结果表明,GIA对GRACE监测的等效水柱变化有重大影响,较大的GIA影响出现在西南极,沿罗斯冰架-卡姆布冰流-罗尼冰架-南极半岛分布,最大值在卡姆布冰流,达到29.8 mm/a;GIA对南极整体冰质量平衡的影响达到134±28 Gt/a.在不确定性的方差中,西南极和东南极分别以冰负荷模型差异和地幔黏滞度差异影响为主,对整个南极,冰模型差异影响占88.4%;在一些典型地区,GRACE监测的等效水柱在扣除GIA前后分别是,卡姆布冰流~32.8 mm/a和~6.3 mm/a,阿蒙森海湾~-95.3 mm/a和~-102.5 mm/a,Enderby Land~13.6 mm/a和~8.1 mm/a.整个南极冰盖总质量变化在扣除GIA贡献后为-82±29 Gt/a,该估计与卫星测高结果较吻合.此外,GIA对卫星测高监测的冰面高程变化的影响一般不超过8%.本研究为空间大地测量监测南极冰质量平衡提供了新的改正模型.

... 由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^[6,7]、极地冰盖质量变化^[8,9,10]等方面的研究 ...

2012

38.597

0.0

. 2012, 491(7425):586-589

Lower satellite-gravimetry estimates of Antarctic sea-level contribution

Recent estimates of Antarctica’s present-day rate of ice-mass contribution to changes in sea level range from 31 gigatonnes a year (Gt yr −1 ; ref. 1 ) to 246 Gt yr −1 (ref. 2 ), a range that cannot be reconciled within formal errors 3 . Time-varying rates of mass loss 2 , 4 , 5 , 6 contribute to this, but substantial technique-specific systematic errors also exist 3 . In particular, estimates of secular ice-mass change derived from Gravity Recovery and Climate Experiment (GRACE) satellite data are dominated by significant uncertainty in the accuracy of models of mass change due to glacial isostatic adjustment 7 , 8 (GIA). Here we adopt a new model of GIA, developed from geological constraints, which produces GIA rates systematically lower than those of previous models, and an improved fit to independent uplift data 9 . After applying the model to 99 months (from August 2002 to December 2010) of GRACE data, we estimate a continent-wide ice-mass change of −69 ± 18 Gt yr −1 (+0.19 ± 0.05 mm yr −1 sea-level equivalent). This is about a third to a half of the most recently published GRACE estimates 2 , 5 , which cover a similar time period but are based on older GIA models. Plausible GIA model uncertainties, and errors relating to removing longitudinal GRACE artefacts (‘destriping’), confine our estimate to the range −126 Gt yr −1 to −29 Gt yr −1 (0.08–0.35 mm yr −1 sea-level equivalent). We resolve 26 independent drainage basins and find that Antarctic mass loss, and its acceleration, is concentrated in basins along the Amundsen Sea coast. Outside this region, we find that West Antarctica is nearly in balance and that East Antarctica is gaining substantial mass.

... 由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^[6,7]、极地冰盖质量变化^[8,9,10]等方面的研究 ...

2013

0.0

... 由于其数据的高精度和高时空分辨率全球覆盖,GRACE时变重力数据被广泛的应用于陆地水变化^[6,7]、极地冰盖质量变化^[8,9,10]等方面的研究 ...

1972

0.0

. 1972, 10(3):761-797

Deformation of the Earth by surface loads

W. E. Farrell

> The static deformation of an elastic half-space by surface pressure is reviewed. A brief mention is made of methods for solving the problem when the medium is plane stratified, but the major emphasis is on the solution for spherical, radially stratified, gravitating earth models. Love-number calculations are outlined, and from the Love numbers, Green's functions are formed for the surface mass-load boundary-value problem. Tables of mass-load Green's functions, computed for realistic earth models, are given, so that the displacements, tilts, accelerations, and strains at the earth's surface caused by any static load can be found by evaluating a convolution integral over the loaded region.

... 而根据弹性负荷理论^[11],由GRACE时变重力数据不仅能够得到地表质量负荷变化引起的重力场变化,也能够估算地表负荷变化所引起的地表垂直形变^[12] ...

... 在目前利用重力卫星GRACE估算地表垂直负荷形变的计算中^[13,14,15],一般采用基于PREM（Preliminary Reference Earth Model）地球模型^[16]得到的负荷勒夫数^[11,17], 但该模型使用的是全球平均的弹性结构参数（密度、P波速度、S波速度等）,不能很好地反映中国大陆特别是青藏高原巨厚的地壳结构 ...

2010

0.0

. 2010, 53(5):1091-1098 DOI:10.3969/j.issn.0001-5733.2010.05.009

Climate-driven annual vertical deformation of solid Earth calculated from GRACE

1 Key Laboratory of Dynamic Geodesy, Institute of Geodesy & Geophysics, Chinese Academy of Sciences, Wuhan 430077, China 2 Graduate University, Chinese Academy of Sciences, Beijing 100049, China

Atmosphere, ocean and continent water mass seasonal variations cause variation in surface deformation, which is detectable using Gravity Recovery and Climate Experiment and GPS observation. Comparing with surface deformation simulated from atmosphere, ocean and continent water models, the deformation derived from GRACE has no errors related with accuracy uncertainty of models. Climate-driven seasonal vertical deformation signals of the solid Earth in China and neighboring areas are calculated from GRACE monthly time-variable gravity field coefficients truncated to degree and order 60, and the results are compared with seasonal signals measured at 42 GPS sites located in the same region. In calculating we use De-stripes and De-stripes plus a 3×105 m Gaussian smoothing respectively, and we find the former filtering result is better than the latter one. In the annual vertical crustal deformation from GRACE using De-stripes, we find at all GPS sites the amplitudes and phases of deformation from GRACE are close to those from GPS observations. Obvious discrepancy at some sites suggests that it might be caused by a local geophysical process or GPS site analysis error and GPS time series discontinuity. In the mainland of China and neighboring areas the smallest amplitude of deformation of about 1×10 -3 m is in the southeast of site TASH and the greatest amplitude of deformation of 10×10 -3 m in the region of Ganges-Lancang River Basin. These results demonstrate that GRACE can be a new effective tool for monitoring annual vertical deformation on a large scale in China and neighboring areas.

卫星重力和GPS测量技术可以监测地表流体(大气、海洋和陆地水)质量季节性迁移引起的地表周年形变；与陆地水等地表流体模型综合模拟的地表形变相比，卫星重力的形变监测结果避免了模型的精度不确定性带来的误差.本文利用前60阶GRACE卫星时变重力资料和“去相关”、组合滤波两类滤波方法分别解算了中国及邻区的地表季节性垂直形变，并与区内42个GPS台站上观测到的季节性信号进行了比较，发现采用“去相关”滤波方法处理后的结果优于采用组合滤波处理后的结果.文中采用“去相关”滤波方法，GRACE解算的周年垂直形变的振幅、相位和GPS结果总体上一致；少数站上GRACE和GPS得到的振幅或相位相差较大，主要因素可能与GPS解算策略、GPS观测资料的连续性或局部大气、水文过程等地球物理因素有关.在中国及邻区的陆地上GRACE解算的周年垂直形变的振幅最小值出现在TASH台站东南，约1×10 -3 m；最大值出现在恒河—澜沧江流域，可达10×10 -3 m.文中的结果证实了在中国及邻区可以用GRACE卫星重力这种新手段监测大尺度的地表周年垂直形变.

2012

0.0

2005

0.0

2012

0.0

1.292

. 2012, 32(2):32-38

Seasonal variations of Earth’s surface deformation estimated from GPS and satellite gravimetry

1)Shanghai Astronomical Observatory, CAS, Shanghai 200030;2)Graduate University of the Chinese Academy of Sciences, Beijing 100049

We computed and compared the vertical loading deformation from GPS and GRACE and found that at most global sites, the root mean square (RMS）of GPS coordinate time series decreased after removing the GRACE estimates, and the annual variations of the GPS height at most sites also agree well with GRACE or geophysical model estimates in the amplitude and phase.It indicates that the nonlinear seasonal GPS vertical variation is mainly caused by the geophysical loads. However, at some sites, particularly in the Antarctica, some ocean coasts and small peninsulas, large discrepancy has been found between theestimates with the two techniques. We analyzed and discussed the error sources of the discrepancies between GPS and GRACE and their effects, which isproved by a good agreement with geophysical models, and the remaining disagreement may be due to the GPS technical errors. It needs to further investigate using longer and more GPS and GRACE measurements.

估计和比较GPS和GRACE得到的地表垂直负荷形变，发现全球大部分地区，扣除GRACE地表位移后GPS垂直坐标时间序列均方根(RMS)减小，而且二者周年变化的相位和振幅大部分地区具有较好一致性，反映GPS高程非线性季节性变化主要是由地表质量负荷引起的。然而在某些区域，特别是南极洲、海岸带附近和小岛屿，二者之间存在较大的偏差。分析和讨论两种技术中可能引入的各种误差源及其影响得出，GRACE负荷形变估计影响较小，这与地球物理模型估计的一致性得到了验证，因而剩下偏差是否由GPS本身技术误差所引起，还有待新的高分辨率重力卫星和更多GPS观测和新模型的进一步研究。

1981

2.383

0.0

. 1981, 25(4):null-null

Preliminary reference Earth model

1996

0.0

0.5277

. 1996, 39(Suppl.):182-189

Improvement of computation of load Love numbers of SNREI Earth model

Laboratory of Dynamical Geodesy, Institute of Geodesy and Geophysics, Academia Sinica, Wuhan430077, China

In this paper,on basis of the deformation theory of SNREI elastic earth model under surface load developed by Longman（1962） and Farrell（1972） we focused our attention on the numerical methods and the result analyses of love numbers. First, we employed a new transformation,rn factor method which is much briefer than traditional dimensionless method, and is also of high computational precision. Second, for evaluating numerical results we explicitly put forward an effective criterion which includes surface boundary condition,linearity of integrating differential equation, and convergence.Finally,we obtained a series of precise computation results of PREM model.

基于Ｌｏｎｇｍａｎ和Ｆａｒｒｅｌｌ的表面负荷形变理论，深入研究计算ＳＮＲＥＩ弹性地球模型表面负荷勒夫数的数值计算方法，取得新的进展：采用了一种新的代换方法─ｒ￣ｎ因子法，比传统的无量纲化法简单易行，且能达到很高的计算精度；确立了检验表面边界条件、微分方程积分线性性和计算结果的收敛性，用于评价数值计算结果精度的有效准则；给出了ＰＲＥＭ地球模型的一组高精度计算结果．

2013

0.0

... 而根据Wang等^[18]利用水文模拟数据的研究,区域地壳结构对GPS估算地表质量负荷的影响不容忽视 ...

... 这是由于M-PREM模型中地壳结构的密度、P波速度以及S波速度都要比PREM模型的小一些,进而M-PREM模型相应的弹性Lame常数也比PREM模型的要小^[18] ...

0.0

... Laske等^[19]发展的Crust2 ...

2012

1.675

0.0

... 然后分别基于M-PREM和PREM 2个地壳结构不同的地球模型,我们计算了负荷勒夫数h_l和k_l,具体方法可参见相关文献^[20],其中h_l是与垂直位移有关的负荷勒夫数,而k_l是和重力变化有关的负荷勒夫数 ...

2013

0.0

... 虽然RL05数据较之前的RL04数据在空间分辨率和精度上都有所提高,“条带”误差明显减小^[21],但还需要数据后处理来提高信噪比以满足研究需要 ...

2006

0.0

... 首先将每月重力场系数扣除观测时段的均值,然后采用Chambers提出的P3M10方法^[22]对扣除均值的GRACE重力场系数进行去相关处理,最后利用对真实信号影响较小^[23]的高斯滤波^[24]对去相关后的系数进行空间平滑,用以压制重力卫星观测数据的高阶误差 ...

2010

2.853

0.0

1998

0.0

. 1998, 103(B12):30205-30229

Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE

John WahrMery MolenaarFrank Bryan

> The GRACE satellite mission, scheduled for launch in 2001, is designed to map out the Earth's gravity field to high accuracy every 2–4 weeks over a nominal lifetime of 5 years. Changes in the gravity field are caused by the redistribution of mass within the Earth and on or above its surface. GRACE will thus be able to constrain processes that involve mass redistribution. In this paper we use output from hydrological, oceanographic, and atmospheric models to estimate the variability in the gravity field (i.e., in the geoid) due to those sources. We develop a method for constructing surface mass estimates from the GRACE gravity coefficients. We show the results of simulations, where we use synthetic GRACE gravity data, constructed by combining estimated geophysical signals and simulated GRACE measurement errors, to attempt to recover hydrological and oceanographic signals. We show that GRACE may be able to recover changes in continental water storage and in seafloor pressure, at scales of a few hundred kilometers and larger and at timescales of a few weeks and longer, with accuracies approaching 2 mm in water thickness over land, and 0.1 mbar or better in seafloor pressure.

2012

0.0

... 根据GRACE观测的时变重力场球谐系数,可由以下公式计算地表质量驱动的垂直负荷形变^[1],具体推导过程可参见相关文献^[25]： ...

2012

0.0

1.388

. 2012, 27(3):337-346

Comparison of the precipitation cycle and trend in different areas of Northern China in recent 50 years

1.Key Laboratory of Land Surface Process and Climate Change in Cold and Arid Regions,Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou730000, China; 2. Graduate University of Chinese Academy of Sciences, Beijing100049, China; 3.College of Global Change and Earth System Science, Beijing Normal University, Beijing100875, China

Based on division, precipitation cycle and trend in different areas of Northern China (NC) are analyzed and compared by using wavelet analysis and singular spectrum analysis based on the monthly precipitation data of 243 stations in the northern part of China during 1958-2009. The study results show that the precipitation in Northwest China (Qinghai Area and Arid Area) has stronger tendency than that in the Eastern NC and Middle NC. From the late 1950’s to 1960’s the precipitation in Eastern NC and Middle NC was on high side, while it was on low side in Qinghai and Arid Area at that time. During the 1980’s, the precipitation in Middle NC turned from high side to low side, while it turned reversely in the other three areas. The turning point and the lasting time were different in different areas. In recent several years, the precipitation has increased in Eastern NC, Middle NC and Qinghai area, and decreased in Arid Area. Except for Qinghai area, precipitation in Northern China has longer period than 10 years—22 a in Eastern NC, 15 a in Middle NC and 11 a in Arid Area—that has became stable and significant since the 1980’s. Northern China’s precipitation, in common, has a period of 2~3 a and 5 a. The oscillation amplitude has obvious inter-annual and inter-decadal variability, which is quasiperiodic. 

对中国北方243个站点1958—2009年逐月降水资料，采用小波分析和奇异谱分析（SSA）方法，在分4区基础上，对北方不同地区降水的周期和趋势进行分析，并进行比较。结果表明，西北地区（青海区、干旱区）降水的趋势性比北方中、东部区的明显。北方中、东部区在20世纪50年代末到60年代相对多雨，而青海区、干旱区在20世纪50年代末到70年代末或80年代中相对少雨。在20世纪80年代，北方中部区降水由偏多转为偏少，而其余3个区域（北方东部区、青海区、干旱区）的降水由偏少转为偏多，发生和持续时间各不相同。近几年，北方东部区、北方中部区、青海区的降水增加，而干旱区降水下降。北方东部区、中部区、干旱区存在10年以上的长周期，北方东部区为准22年，北方中部区为准15年，干旱区为准11年，这种长周期在20世纪80年代之后变得规则且稳定。北方降水普遍存在准2~3年周期和准5年周期，其振幅有明显的年际、年代际变化，具有一定的周期性。

... 除了降水等自然因素的影响^[26],人为因素也会对地表质量分布产生很大的影响,从而造成地表垂直负荷形变速率的变化 ...

2013

3.982

0.0

. 2013, 40(15):3924-3928

Anthropogenic impacts on mass change in North China

Qiuhong Tang 1,* ,Xuejun Zhang 1,2 andYin Tang 1

1 Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, China 2 University of Chinese Academy of Sciences, Beijing, China * Corresponding author: Q. Tang, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, No. 11A, Datun Rd., Chaoyang District, Beijing 100101, China. ( tangqh@igsnrr.ac.cn )

> [1] The gravity fields from the Gravity Recovery and Climate Experiment (GRACE) satellite have been used to estimate groundwater depletion in many parts of the world. Groundwater depletion assessment in North China, however, is affected by large anthropogenic disturbance on mass variation. Using the water survey data and coal flow statistics, we show that the mass variations in North China during 2003–2011 were largely affected by reservoir regulation, water diversion, and coal transport. According to our estimates, the mass loss rate of groundwater depletion (−14 to −8.4 mm yr −1 ) was largely offset by the mass gains caused by reservoir regulation (1.3 mm yr −1 ), water diversion (4.4 mm yr −1 ), and coal transport (1.9 mm yr −1 ) in the North China Plain. We note that anthropogenic impacts on mass change must be taken into account when using the GRACE data to estimate groundwater change in the area intensively altered by human activities.

... 例如华北地区地下水抽取、煤矿开采等因素都会造成该地区地表质量流失^[27,28],在图4中表现为明显的垂直形变正速率 ...

2013

0.0

1.388

. 2013, 28(8):923-929

Research on spatial and temporal distribution of the precipitation infiltration amount over the past 50 years in North China Plain

Key Laboratory of Groundwater Pollution Mechanism and Remediation, Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geologcal Sciences, Shijiazhuang 050061, China

In the light of characteristics of North China Plain such as hydrogeological conditions, high degree utilization of groundwater, remarkable differences in buried depth of groundwater, aerated zone and on the basis of large quantities of drilling and groundwater level monitoring data, we divided the North China Plain into four hydrogeological units, considering the depth of 7 meters as the precipitation infiltration boundaries and endowed drilling strata with infiltration coefficient according to the hydrogeological conditions of partitions, and obtained the precipitation infiltration coefficient distribution in the 1960s, 1980s and 2000s using weighted average method. The results indicate that the precipitation infiltration coefficient tends to increase with the decline of groundwater level. Although precipitation has a decrease tendency in nearly 50 years, the precipitation infiltration increased due to the infiltration coefficient. The precipitation infiltration amount were 118.86×10 8 , 147.91×10 8 , 174.33×10 8 m 3 in the 1960s, 1980s and 2000s.

针对华北平原水文地质条件复杂，地下水开发利用程度高，地下水位埋深和包气带岩性在时间和空间上差异大的特点，基于大量钻孔和地下水位监测资料，将华北平原划分为4个水文地质单元，以埋深7 m作为降水入渗稳定点，根据各分区的水文地质条件对钻孔岩层赋予入渗系数值，应用加权平均法求得华北平原20世纪60年代、80年代和21世纪初的降水入渗系数分布图。利用华北平原1956—2008年水资源四级区逐月降水量数据，求得华北平原20世纪60年代、80年代和21世纪初各分区单元的降水入渗量。结果表明，50多年来华北平原降水量呈减少的趋势，降水入渗系数呈增加的趋势，降水入渗量呈增加的趋势。3个年代的降水入渗量分别是118.86×10 8 ，147.91×10 8 和174.33×10 8 m 3 。

... 例如华北地区地下水抽取、煤矿开采等因素都会造成该地区地表质量流失^[27,28],在图4中表现为明显的垂直形变正速率 ...

2011

3.149

0.0

... 而三峡水库的蓄水^[6,29]则造成该地区垂直负荷形变负异常 ...

2006

3.982

0.0

... 而根据Wahr等^[30]的类似评估方法,我们估算了GRACE监测中国大陆地表垂直负荷形变速率的误差,其最大值约为0 ...