EnKF同化的背景误差协方差矩阵局地化对比研究

引用本文

韩培, 舒红, 许剑辉. EnKF同化的背景误差协方差矩阵局地化对比研究. 地球科学进展, 29(10): 1175-1185
Han Pei, Shu Hong, Xu Jianhui. A Comparative Study of Background Error Covariance Localization in EnKF Data Assimilation. Advances in Earth Science, 29(10): 1175-1185 复制到剪切板

Permissions

This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

EnKF同化的背景误差协方差矩阵局地化对比研究

韩培, 舒红, 许剑辉

1.武汉大学测绘遥感信息工程国家重点实验室,湖北武汉 430079

作者简介：韩培(1989-),女,湖北孝感人,硕士研究生,主要从事遥感数据同化研究. E-mail: 1129143892@qq.com

基金:江苏省苏州市科技计划项目“气象观测数据分析的时空统计软件”(编号：SYG201319); 国家自然科学基金项目“时空交互的统计建模”(编号：41171313)资助

摘要

在集合数据同化中,背景场误差的协方差估计特别重要。通常有限个成员的集合在估计背景误差协方差矩阵时会引入伪相关,从而造成协方差被低估、滤波发散。虽然协方差膨胀的经验性方法能一定程度缓解协方差被低估的问题,但不能消除协方差的伪相关问题。因此,结合EnKF方案探讨2种消除伪相关的局地化方法(协方差局地化方法和局地分析方法),分析这2种局地化方法对背景误差协方差矩阵、增益矩阵、集合转换矩阵以及同化结果的影响。实验结果表明：局地化方法不仅能消除背景误差协方差矩阵的伪相关,还可以增加背景误差协方差矩阵的秩;在“弱”同化强度下,2种局地化方法的增益矩阵和集合转换矩阵相等;随着同化强度的增大,增益矩阵和集合转换矩阵的差异会变大;在不同的同化强度下,2种局地化方法各具特色,相对而言,协方差局地化方法在更新集合均值和集合扰动上具有较强的鲁棒性。研究结论有助于背景场误差协方差的精细分析和估计。

关键词: EnKF; 协方差局地化; 局地分析; 伪相关

中图分类号:P237 文献标志码:A 文章编号:1001-8166(2014)10-1175-11

A Comparative Study of Background Error Covariance Localization in EnKF Data Assimilation

Han Pei, Shu Hong, Xu Jianhui

1.State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079,China

Abstract

In ensemble data assimilation, the estimate of background error covariance is particuarly important. In general, the use of a finite ensemble size for estimating the background error covariance matrix easily introduces spurious correlations, which leads to the underestimation of covariance and filter divergence. Covariance inflation is an empirical method of correcting the underestimation of background error covariance, but it does not help to solve the problem of long-range spurious correlations. Therefore, based on the EnKF scheme, we explored two localization methods to eliminate the spurious correlations, which were the covariance localization method and the local analysis method. We analyzed their impacts on the background error covariance matrix, gain matrix, ensemble transform matrices and data assimilation results. The experimental results have been obtained. That is, the localization method not only can remove the spurious covariance in the background error covariance matrix, but also can increase the rank of the matrix. In a “weak” assimilation, the gain matrix and ensemble transform matrices of two methods are very close, but the differences of the gain matrix and ensemble transform matrices become more evident with the increase of assimilation strength. Under the different strength of assimilation, two localization methods have their own characteristics, and relatively the covariance localization method has stronger robustness on the update of ensemble mean and ensemble anomalies. This study is very helpful for the fine analysis and estimate of the background error covariance.

Keyword: EnKF; Covariance localization; Local analysis; Spurious correlations.

Show Figures

1 引言

卡尔曼滤波(Kalman Filter, KF)是顺序同化算法的最早形式和理论基础, 在线性系统和高斯白噪声下能得到无偏最优估计, 但大气海洋预报模式多数是非线性系统, KF必须进行扩展才能适用^[1]。1994年Evensen^[2]在海洋资料同化过程中, 首次用到集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)。它是集合预报和KF的有效结合, 利用集合来存储、传播、更新状态估计量和状态误差协方差, 克服了传统KF应用中的不足, 同时有效地降低了同化过程中的计算量, 被广泛应用于大规模数据同化系统, 并逐步与变分方法结合^[3]。

在集合数据同化中, 将模型预测结果作为下一同化时刻的背景场时, 模型误差由背景场误差来表现, 误差的空间相关性由背景场误差的协方差矩阵(非对角阵)来表达。2个同化时刻之间的间隔时间比较短, 通常假设观测误差由误差的方差(对角阵形式的观测误差协方差矩阵)来表达, 观测误差通过背景场误差的协方差矩阵来传递空间相关信息到最终的同化分析结果中。因此, 背景场误差协方差的估计非常重要。然而, 有限个成员的集合在估计背景误差协方差矩阵时会引入伪相关^[4], 即在物理上不相关或空间上距离较远的状态变量之间存在伪相关。随着同化过程的进行, 背景误差协方差被系统地低估, 观测数据的权重越来越小, 最终完全被忽视, 导致滤波发散^[5]。这样估计得到的分析值不能准确地反映系统的真实状态。为了减少伪相关对同化过程的影响, 改善同化结果, 相关学者提出了协方差膨胀和局地化2种方法^[6]。

协方差膨胀是由Anderson等^[7]于1999年提出的, 用来修正背景误差协方差矩阵被低估的方法。其原理是利用一个膨胀因子r来增大背景误差协方差, 从而消除背景误差协方差被低估的现象。目前, r的选择都是经验性的。这种方式会打破系统的物理平衡, 不能消除远距离的伪相关^[8]。因此, 引入背景误差协方差局地化方法的研究是非常必要的。在同化过程中, 局地化方法能够减少观测数据对空间区域的影响, 减少参与计算的集合大小。

目前, 广泛应用的局地化方法有2种, 即协方差局地化方法(Covariance Localization, CL)和局地分析方法(Local Analysis, LA)。虽然曾有学者研究过它们之间的关系, 但他们仅仅只考虑了2种方法对单个变量的影响^[9]。这里我们不仅考察和分析2种局地化方法对背景误差协方差矩阵P^f、增益矩阵K和集合转换矩阵T的影响。此外, 还基于EnKF、EnSRF和DEnKF同化方案, 对比和分析这2种局地化方法对同化结果的影响。

2 理论背景

2.1 EnKF

KF更新方程如下:

$\begin{matrix} \begin{matrix} x^{a} = x^{f} + K (d - H x^{f}) (1) \\ P^{a} = (I - KH) P^{f} (2) \\ K = P H^{T} (HP H^{T} {+ R)}^{- 1} (3) \end{matrix} \end{matrix}$

式中:x是状态估计值, 上标f和a分别表示预测和分析, K是卡尔曼增益, d是观测向量, H是观测算子, P是状态误差协方差矩阵, I是单位矩阵, R是观测误差协方差矩阵, 上标T表示矩阵转置。在EnKF中, 状态估计值x和状态误差协方差矩阵P是用模型状态集合E表示:

$x = \frac{1}{m} E 1 (4)$

$P = \frac{1}{m - 1} A A^{T} (5)$

式中:m为集合大小, E是包含所有集合成员的矩阵, 1是所有元素均为1的向量, A是集合扰动:

$\begin{matrix} A = E (I - \frac{1}{m} 11^{T}) (6) \end{matrix}$

在EnKF中应用局地化有2个原因:空间伪相关和集合非满秩^{[10, 11]}问题。在同化分析过程中, 它们会导致背景误差协方差减小过快、滤波发散。

2.2 协方差局地化(Covariance Localization, CL)

CL是一种协方差滤波方法, 利用局地化半径来截断背景误差协方差矩阵中远距离的伪相关, 改善背景误差协方差矩阵的估计质量。常采用舒尔积^[12], 即通过一个基于距离的相关系数矩阵ρ ^{[6, 13]}与背景误差协方差矩阵P^f作舒尔积, 来替代原有P^f, 如式(7)：

P^f→ ρ 。P^f (7)

CL只适用以下方案, 如：传统EnKF、EnSRF(Ensemble Square Root Filter, EnSRF)^[14]、DEnKF(Deterministic Ensemble Kalman Filter, DEnKF)^[15], 而不适用于ETKF(Ensemble Transform Kalman Filter, ETKF)^[16]。

2.3 局地分析(Local Analysis, LA)

与CL方法不同, LA方法适用任何独立方案, 原理是以待更新状态变量为中心, 建立一个虚拟局部窗口, 得到该状态变量背景误差协方差的局部近似值, 这等价于在更新过程中, 设定局部窗口外的集合扰动为零。在ETKF方案中, 第i个状态变量的局部更新过程如下:

$\begin{matrix} \begin{matrix} x_{i}^{a} = x_{i}^{f} + {\overset{i}{K}}_{i, :} (\overset{i}{d} - \overset{i}{H} {\overset{i}{x}}^{f}) (8) \\ A_{i, :}^{a} = A_{i, :}^{f} \overset{i}{T} (9) \end{matrix} \end{matrix}$

在ETKF中, 卡尔曼增益 $\begin{matrix} \overset{i}{K} \end{matrix}$ 和集合转换矩阵 $\begin{matrix} \overset{i}{T} \end{matrix}$ 表示如下:

$\begin{matrix} \overset{i}{S} \equiv {\overset{i}{R}}^{- 1 / 2} \overset{i}{H} {\overset{i}{A}}^{f} / \sqrt[]{m - 1} (10) \end{matrix}$

$\begin{matrix} {\overset{i}{K}}_{i, :} = A_{i, :}^{f} {\overset{i}{S}}^{T} (I + \overset{i}{S} {\overset{i}{S}}^{T})^{- 1} {\overset{i}{R}}^{- 1 / 2} / \sqrt[]{m - 1} \end{matrix}$ (11)

$\begin{matrix} \overset{i}{T} = (I + {\overset{i}{S}}^{T} {\overset{i}{S})}^{- 1 / 2} \end{matrix}$ (12)

式中:上标i表示局部; $\begin{matrix} \overset{i}{A} \end{matrix}$ 是局部集合扰动, 用于更新第i个状态变量或集合扰动矩阵A的第i行; A_i_{, :}为扰动矩阵A的第i行; $\begin{matrix} \overset{i}{K} \end{matrix}$ 为局部卡尔曼增益; $\begin{matrix} {\overset{i}{K}}_{i, :} \end{matrix}$ 为 $\begin{matrix} \overset{i}{K} \end{matrix}$ 的第i行; $\begin{matrix} \overset{i}{H} \end{matrix}$ 是局部观测算子; $\begin{matrix} \overset{i}{d} \end{matrix}$ 是局部观测向量; $\begin{matrix} \overset{i}{T} \end{matrix}$ 是局部集合转换矩阵; $\begin{matrix} \overset{i}{S} \end{matrix}$ 是局部集合观测扰动; $\begin{matrix} \overset{i}{R} \end{matrix}$ 是局部观测误差协方差; x是状态向量; x_i是第i个状态变量。

2.4 2种方法的比较分析

2.4.1 集合均值的更新

EnKF中, 第i个状态变量的更新方程如下:

$\begin{matrix} x_{i}^{a} = x_{i}^{f} + {\overset{i}{K}}_{i, :} (\overset{(i)}{d} - \overset{(i)}{H} {\overset{(i)}{x}}^{f}) (13) \end{matrix}$

上标圆括号表示渐变, 这取决于所选的方法, 对于CL有:

(14)

此时局部卡尔曼增益为：

(15)

将公式(15)与公式(11)比较, 可知:①在CL中, 矩阵求逆项[I+(Hρ H^T)􀳱(SS^T)]^-1R^-1/2是全局的, LA中矩阵求逆项

是局部的; ②当同化很“ 弱” 时, 即‖ (Hρ H^T)􀳱(SS^T)‖ < < ‖ I‖ , 2种方法的

近似相等, 但一般它们不相等; ③在CL中, d, H和x向量是不变的, 而LA中是渐变的, 两者更新的差异依赖于K随观测点到待更新点距离衰减的速率。当观测点到待更新点的距离大于局地化半径时, 观测数据本身对待更新状态变量的影响很小, 此时它们的变化就不那么重要了。

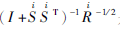
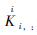
2.4.2 集合扰动的更新

在EnSRF中, 集合扰动的更新如公式(16)和公式(17)所示:

$\begin{matrix} \begin{matrix} A^{a} = T A^{f} (16) \\ T = {(I - KH)}^{\frac{1}{2}} (17) \end{matrix} \end{matrix}$

由矩阵求逆引理^[17], 得到T, 如公式(18):

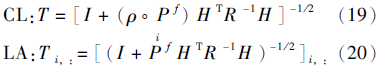
$\begin{matrix} T = (I + P^{f} H^{T} R^{- 1} {H)}^{- 1 / 2} (18) \end{matrix}$

对于CL和LA, T分别如下:

尽管上述T的形式不同, 但是对于待更新变量行, 它们是一致的, 因为:

$\begin{matrix} [\overset{p}{\sum_{o = 1}} {\overset{io}{A}}^{f} ({\overset{io}{A}}^{f})^{T} {\overset{{o}}{H}}^{T}]_{i, :} = [{\overset{i}{A}}^{f} ({\overset{i}{A}}^{f})^{T} H^{T}]_{i, :} \end{matrix}$ (21)

式中:p是观测数目; H是观测算子; $\begin{matrix} \overset{{o}}{H} \end{matrix}$ 表示第o行元素为0, 其他行元素和H相同的矩阵; io是第o个观测数据的位置; $\begin{matrix} \overset{io}{A} \end{matrix}$ 是以io为中心的局部集合扰动。

故：

(22)

将式(19)、(20)由泰勒级数展开, O(.)表示是佩亚诺余项：

CL：

(23)

LA:

(24)

结合式(22)可知：同化很“ 弱” 时, CL和LA的T近似相等, 但一般两者的T不相等。

3 实验方案

3.1 线性平流模型

线性平流(Linear Advection, LA)模型^[18]具有一维周期性, 状态向量X维度为n, 如下:

$\begin{matrix} X (t) = [x_{1} (t), \dots, x_{n} (t)], t = 1, 2, \dots, n \end{matrix}$ (25)

$\begin{matrix} x_{i} (t + 1) = \begin{matrix} x_{i - 1} (t), i = 2, \dots, n \\ x_{n} (t), i = 1 \end{matrix} (26) \end{matrix}$

状态样本x_i是由n_k个具有随机振幅和相位的正弦波组合而成, 如下:

$\begin{matrix} x_{i} = \overset{n_{k}}{\sum_{k = 1}} a^{(k)} \sin (\frac{2 πk}{n} i + φ^{(k)}), 1 \leq i \leq n \end{matrix}$ (27)

$\begin{matrix} \begin{matrix} a^{(k)} = rand () \exp [- \frac{1}{2} {(\frac{k - k_{\max}}{k_{ω}})}^{2}] (28) \\ φ^{(k)} = rand () \times 2 π (29) \end{matrix} \end{matrix}$

rand()函数返回均匀分布的随机数, 且0≤ rand()≤ 1, exp()为e的指数函数。

3.2 实验设计

3.2.1 基本参数

设定LA模型的状态变量数n=100, k_ω=k_max=10, n_k=50。集合成员数m为21, 观测数目为45, 同化总步长为1 500, 同化间隔步长为5, 局地化半径R_loc为10, 不加任何说明时, 观测方差为0.1。实验中采用传播减小因子k_σ来评估同化强度^[9], 其表达式如下:

$\begin{matrix} \begin{matrix} k_{σ} = σ^{f} / σ^{a} (30) \\ σ = \sqrt[]{tr (HP H^{T})} (31) \end{matrix} \end{matrix}$

当k_σ-1≪1时, 同化强度定义为“ 弱” 同化, 即在更新状态变量的过程中, 观测信息占的权重远小于模型预测信息, 观测数据的贡献较小。当k_σ-1≫1时, 同化强度定义为“ 强” 同化, 即在更新状态变量时, 观测信息占的权重远大于预测信息, 引入的观测信息较多。当k_σ-1与1相差不大时, 同化强度定义为“ 中” 同化, 即观测信息和预测信息权重相当。另外, 实验采用集合均方根误差(RMSE)和集合传播(spread)来评估同化效果, EnKF同化过程和效果图如图1所示。

3.2.2 局地裁剪函数

局地裁剪函数是由高斯和科恩于1999年提出的^[19], 其表达式如下：

$\begin{matrix} ρ = \{\begin{matrix} 1 - \frac{5}{3} {(| z |/ c)}^{2} + \frac{5}{8} {(| z |/ c)}^{3} + \frac{1}{2} {(| z |/ c)}^{4} - \frac{1}{4} {(| z |/ c)}^{5}, 0 \leq | z |\leq c \\ - \frac{2}{3} {(| z |/ c)}^{- 1} + 4 - 5 (| z |/ c) + \frac{5}{3} {(| z |/ c)}^{2} + \frac{5}{8} {(| z |/ c)}^{3} - \frac{1}{2} {(| z |/ c)}^{4} + \frac{1}{12} {(| z |/ c)}^{5}, c \leq | z | \leq 2 c \\ 0, 2 c \leq | z | \end{matrix} (32) \end{matrix}$ 式中:z表示网格点之间的距离或者网格点与观测点之间的距离, c是尺度范围, c= $\begin{matrix} \sqrt[]{\frac{10}{3}} \end{matrix}$ R_loc, 局地化半径R_loc=10。

	Figure Option View Download New Window
	图1 EnKF同化过程和效果图Fig.1 The process and result of data assimilation based on EnKF

4 实验结果与分析

4.1 CL和LA对背景误差协方差矩阵P^f的影响

为了研究CL对背景误差协方差矩阵P^f的影响, 提取同化时刻t=50时的P^f和ρ 。P^f作比较, 结果如图2所示, 其中：图2(a)为状态变量之间的相关系数矩阵ρ , 图2(b)为舒尔积前的背景误差协方差矩阵P^f, 图2(c)为舒尔积后的背景误差协方差矩阵ρ 。P^f。

	Figure Option View Download New Window
	图2 CL对背景误差协方差矩阵P^f的影响色度条表示矩阵元素的取值范围Fig.2 CL’ s impact on the background error covariance matrix P^fColorbar in figure 2 denotes the values range of matrix elements

为了研究LA对背景误差协方差矩阵P^f的影响, 取同化时刻t=50, 第50个状态变量的误差协方差矩阵Pii和P^f作比较, 结果如图4所示。图4(a)是第50个状态变量的裁剪相关系数矩阵Fi, 图4(b)是LA作用前的P^f, 图4(c)是LA裁剪后的Pii, 记为Pla(ii), 图4(c)中的虚线框表示以第50个状态变量为中心的局部区域。

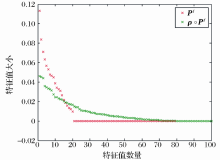	Figure Option View Download New Window
	图 3 舒尔积前后背景误差协方差矩阵P^f的特征值光谱Fig.3 The eigenvalues spectrum of the background error covariance matrixP^fbefore and after Schur Product

	Figure Option P^f (t = 50, i= 50) colorbar in figure 4 denotes the values range of matrix elements '>View Download New Window
P^f (t = 50, i= 50) colorbar in figure 4 denotes the values range of matrix elements '>	图4 LA对背景误差协方差矩阵P^f的影响(t=50, i=50)色度条表示矩阵元素的取值范围Fig.4 LA's impact on the background error covariance matrix P^f (t = 50, i= 50)colorbar in figure 4 denotes the values range of matrix elements

由图4可知：① LA方法可以消除背景误差协方差矩阵P^f中的伪相关, 减少远距离观测数据对待更新状态变量的影响; ② 相对于CL方法, LA方法每次只更新局部区域中心点的协方差, 其他非中心元素的协方差并不更新, 即LA方法中P^f为异步更新, CL方法中P^f是同步更新。

4.2 CL和LA对增益矩阵K的影响

为了研究CL和LA对增益矩阵K的影响, 我们考察了观测误差方差R_{obs_variance}分别为10、10^-1和10^-4这3种情形下EnKF的同化过程, 对应地分别提取同化时刻t=5时未局地化、CL和LA的增益矩阵来对比分析, 3种情形对应的结果分别如图5、6和7所示, 其中：图5(a)、图6(a)和图7(a)是未局地化的增益, 记为Knone; 图5(b)、图6(b)和图7(b)是CL的增益, 记为Kcl; 图5(c)、图6(c)和图7(c)是LA中第50个状态变量的局部增益, 记为Kla(i), 其中虚框表示以第50个状态变量为中心的局部区域; 图5(d)、图6(d)和图7(d)给出了未局地化、CL和LA 3种方法下, 第50个状态变量的增益, 记为Kii。

	Figure Option View Download New Window
	图5 3种增益矩阵K对比图(R_{obs_variance}= 10)色度条表示矩阵元素的取值范围Fig. 5 The contrast of three kinds of gain matrixK (R_{obs_variance} = 10)Colorbar in figure 5 denotes the values range of matrix elements

	Figure Option View Download New Window
	图6 3种增益矩阵K对比图(R_{obs_variance}= 10^-1)色度条表示矩阵元素的取值范围Fig.6 The contrast of three kinds of gain matrix K (R_{obs_variance} = 10^-1)Colorbar in figure 6 denotes the values range of matrix elements

当R_{obs_variance}=10^-1时, k_σ-1≈ 4.4261, 同化强度对应为 “ 中” 同化。由图6可知：① 在“ 中” 同化下, CL的增益矩阵Kcl仍保持对角性, 而LA的局部增益矩阵Kla(i)在局部区域内呈松散状; ② 在“ 中” 同化下, CL和LA更新同一状态变量的增益Kii差异变大, 不像图5(d)中两者差异很小, 由此可知, 随着同化强度的增大, CL和LA的增益差异逐渐变大。

当R_{obs_variance}=10^-4时, k_σ-1≈ 160.958, 同化强度对应为 “ 强” 同化。由图7可知：① 在“ 强” 同化下, CL的增益Kcl仍保持对角性, 但LA的局部增益Kla(i)在局部区域内丧失了对角性, 与图6(c)比较, Kla(i)变得更加松散, 甚至充满整个局部空间; ② 在“ 强” 同化下, CL和LA更新同一状态变量的增益Kii相差很大。

综上可知：① 随着同化强度的增大, CL的增益矩阵始终能保持对角性, 而LA的增益矩阵逐渐会丧失对角性, 因此, CL方法在更新集合均值上具有较强的鲁棒性; ② 在同化很“ 弱” 时, CL和LA的增益近似相等, 但随着同化强度的增大, CL和LA的增益差异变大。

4.3 CL和LA对集合转换矩阵T的影响

由于EnKF的集合扰动更新没有应用到集合转换矩阵T, 这里我们考察观测误差方差R_{obs_variance}分别为10、10^-1和10^-43种情形下EnSRF的同化过程, 对应地分别提取同化时刻t=5时未局地化、CL和LA的集合转换矩阵来比较分析, 3种情形对应的结果分别如图8、9和10所示, 其中：图8(a)、图9(a)和图10(a)是未局地化的集合转换矩阵与单位矩阵之差, 记为Tnone-I; 图8(b)、图9(b)和图10(b)是CL的集合转换矩阵与单位矩阵之差, 记为Tcl-I; 图8(c)、图9(c)和图10(c)是LA中第50个状态变量的局部集合转换矩阵与单位矩阵之差, 记为Tla(i)-I, 其中虚框表示以第50个状态变量为中心的局部区域; 图8(d)、图9(d)和图10(d)给出了未局地化、CL和LA 3种方法下, 第50个状态变量的转换矩阵, 记为T(i)。

	Figure Option View Download New Window
	图7 3种增益矩阵K对比图(R_{obs_variance}= 10^-4)色度条表示矩阵元素的取值范围Fig.7 The contrast of three kinds of gain matrix K (R_{obs_variance} = 10^-4)Colorbar in figure 7 denotes the values range of matrix elements

	Figure Option View Download New Window
	图8 集合转换矩阵T对比图(R_{obs_variance}=10)色度条表示矩阵元素的取值范围Fig.8 The contrast of the ensemble transformation matrix T(R_{obs_variance}= 10)Colorbar in figure 8 denotes the values range of matrix elements

当R_{obs_variance}=10时, k_σ-1≈ 0.2023, 同化强度对应为 “ 弱” 同化。由图8可知：① 未局地化的集合转换矩阵保留了状态变量之间的伪相关, CL和LA消除了集合转换矩阵中远距离的伪相关, 并呈对角性和对称性, 对称性是由模型周期性引起; ② 与CL不同, LA每次只更新区域中心点的T, 其他非中心元素的T均不更新, 即LA中T为异步更新, CL中T为同步更新; ③ 在“ 弱” 同化下, CL和LA更新同一状态变量的转换矩阵T(i)近似相等, 此时两者转换矩阵的差异可忽略。

	Figure Option View Download New Window
	图9 集合转换矩阵T对比图(R_{obs_variance}= 10^-1)色度条表示矩阵元素的取值范围Fig.9 The contrast of the ensemble transformation matrix T(R_{obs_variance}= 10^-1)colorbar in figure 9 denotes the values range of matrix elements

当R_{obs_variance}=10^-1时, k_σ-1≈ 49931, 同化强度对应为 “ 中” 同化。由图9可知：① 在“ 中” 同化下, CL的转换矩阵Tcl仍保持对角性, 而LA的局部转换矩阵Tla(i)在局部区域内呈松散状; ② 在“ 中” 同化下, CL和LA更新同一状态变量的转换矩阵T(i)差异变大, 不像图8(d)中两者差异很小, 由此可知, 随着同化强度的增大, CL和LA的集合转换矩阵差异逐渐变大。

	Figure Option View Download New Window
	图10 集合转换矩阵T对比图(R_{obs_variance}= 10^-4)色度条表示矩阵元素的取值范围Fig.10 The contrast of the ensemble transformation matrix T(R_{obs_variance}= 10^-4)colorbar in figure 10 denotes the values range of matrix elements

当R_{obs_variance}=10^-4时, k_σ-1≈ 183.7845, 同化强度对应为 “ 强” 同化。由图10可知：① 在“ 强” 同化下, CL的转换矩阵Tcl仍保持对角性, 但LA的局部转换矩阵Tla(i)在局部区域内丧失了对角性, 与图9(c)比较, Tla(i)变得更加松散, 甚至充满整个局部空间; ② 在“ 强” 同化下, CL和LA更新同一状态变量的转换矩阵T(i)相差很大。

为了更加清晰对比CL和LA对集合转换矩阵T的影响, 这里给出观测误差方差R_{obs_variance}分别为10和10^-4条件下, 同化时刻t=5, EnSRF同化更新后的全局T, 如图11所示, 其中：Tcl是CL的集合转换矩阵, Tla是LA的全局集合转换矩阵, I是单位矩阵。图11(a)和图11(b)表示观测误差方差R_{obs_variance}=10, t=5时的全局转换矩阵, 图11(c)和图11(d)表示观测误差方差R_{obs_variance}=10^-4, t=5时的全局转换矩阵。

	Figure Option View Download New Window
	图 11 全局集合转换矩阵T对比图(R_{obs_variance}= 10和R_{obs_variance}= 10^-4)色度条表示矩阵元素的取值范围Fig.11 The contrast of the Global ensemble transformation matrix T(R_{obs_variance}= 10 andR_{obs_variance}= 10^-4)colorbar in figure 11 denotes the values range of matrix elements

综上可知：① 随着同化强度的增大, CL的集合转换矩阵始终能保持对角性, 而LA的集合转换矩阵会丧失对角性, 因此, CL在更新集合扰动上有较强的鲁棒性; ② 在同化很“ 弱” 时, CL和LA的集合转换矩阵T近似相等, 但随着同化强度的增大, CL和LA的集合转换矩阵差异变大。

4.4 CL和LA对同化结果的影响

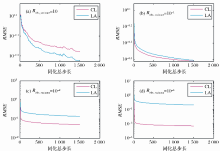
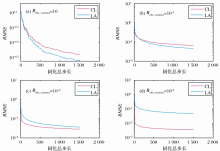
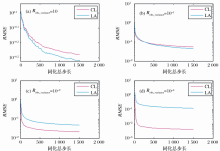
为了研究CL和LA对同化结果的影响, 分别基于EnKF、EnSRF和DEnKF 3种同化方案进行实验, 由于CL不适用于ETKF, 故ETKF在此不作讨论。对上述3种同化方案, 分别考察观测误差方差R_{obs_variance}为10、10^-1、10^-2和10^-4 4种情形, 其中R_{obs_variance}=10时对应于“ 弱” 同化, R_{obs_variance}=10^-1对应于“ 中” 同化, R_{obs_variance}=10^-2和10^-4对应于“ 强” 同化。最终效果图如图12、图13和图14所示, 其中：图12(a)、图13(a)和图14(a)表示观测误差方差R_{obs_variance}为10的同化效果图, 图12(b)、图13(b)和图14(b)表示观测误差方差R_{obs_variance}为10^-1的同化效果图, 图12(c)、图13(c)和图14(c)表示观测误差方差R_{obs_variance}为10^-2的同化效果图, 图12(d)、图13(d)和图14(d)表示观测误差方差R_{obs_variance}为10^-4的同化效果图。

	Figure Option View Download New Window
	图12 基于EnKF的同化效果图Fig.12 The data assimilation effect based on EnKF

	Figure Option View Download New Window
	图13 基于EnSRF的同化效果图Fig.13 The data assimilation effect based on EnSRF

	Figure Option View Download New Window
	图14 基于DEnKF的同化效果图Fig.14 The data assimilation effect based on DEnKF

尽管上述同化方案不同, 但始终存在如下结论：① 在“ 弱” 同化下, LA的同化效果比CL的好; ② 在“ 中” 同化下, 两者的同化效果接近; ③ 在“ 强” 同化下, CL的同化效果比LA的好, 原因是随着同化强度的增大, LA的增益矩阵和集合转换矩阵发生了质变, 失去对角性, 而CL的增益矩阵和集合转换矩阵始终能保持对角性, 这也表明CL在更新集合均值和集合扰动上具有较强的鲁棒性。

5 结论

本文对比分析了2种局地化方法对背景误差协方差矩阵、增益矩阵和集合转换矩阵的影响。此外, 基于EnKF、EnSRF和DEnKF同化方案, 还比较了2种局地化方法对同化结果的影响。实验研究表明：

(1)协方差局地化方法不仅能消除背景误差协方差矩阵中的伪相关, 减少远距离观测数据对待更新状态变量的影响, 而且能增加背景误差协方差矩阵的秩。

(2)相对于CL, LA每次只更新局部区域中心点的集合均值和集合扰动, 其他非中心元素的集合均值和集合扰动并不更新, 即LA为异步更新, CL是同步更新。

(3)在“ 弱” 同化强度下, CL和LA的增益矩阵近似相等, 随着同化强度的增大, 两者的增益差异变大。

(4)在“ 弱” 同化强度下, CL和LA的集合转换矩阵接近, 随着同化强度的增大, 两者的集合转换矩阵差异变大。

(5)随着同化强度的增大, CL的增益矩阵和集合转换矩阵始终能保持对角性, 而LA的增益矩阵和集合转换矩阵会逐渐丧失对角性。同化强度越“ 强” , LA的增益矩阵和集合转换矩阵在空间上越零散, 这表明CL在更新集合均值和集合扰动上具有较强的鲁棒性。

(6)在“ 弱” 同化下, LA的同化效果比CL的同化效果好; 在“ 中” 同化下, CL和LA的同化效果几乎相同; 在“ 强” 同化下, CL的同化效果优于LA, 原因是随着同化强度的增大, LA的增益矩阵和集合转换矩阵发生了质变, 丧失主对角线上的对角性, 而CL的增益矩阵和集合转换矩阵始终能保持对角性, 即CL在更新集合均值和集合扰动上具有较强的鲁棒性。

在大气、海洋、水文和陆面等领域的数据同化应用中, 背景误差协方差的精细分析和估计非常重要, 需要对不同局地化方法进行对比分析和优化选择。通过本文的研究, 我们建议从同化强度、可扩展性和数值计算效率等方面综合考虑局地化方法的选择。特别地, 在同化的强度方面, 如果同化很“ 弱” , LA方法较适合。如果同化很“ 强” , CL方法更具优势。如果同化“ 适中” , 两种方法均可。在可扩展性方面, LA方法允许在集合空间进行分析值的更新, CL方法要求在状态空间进行分析值的更新, 这样造成CL方法不适用于大尺度同化系统。在计算效率方面, CL方法在中尺度同化系统的计算效率方面具有优势, LA方法更适用于并行计算, 这对于大尺度同化系统是一个最佳的选择。目前, 我们通常使用区域分解方式来完成大规模网格的模式数值预报和背景误差协方差的并行计算。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ma Jianwen, Qin Sixian. The research status review of data assimilation algorithm[J]. Advances in Earth Science, 2012, 27(7): 747-757. [马建文, 秦思娴. 数据同化算法研究现状综述[J]. 地球科学进展, 2012, 27(7): 747-757. ] [本文引用:1] [CJCR: 1.388]
[2]	Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research: Oceans (1978-2012), 1994, 99(C5): 10143-10162. [本文引用:1]
[3]	Xiong Chunhui, Zhang Lifeng, Guan Jiping, et al. Development and application of ensemble-variational data assimilation methods[J]. Advances in Earth Science, 2013, 28(6): 648-656. [熊春晖, 张立凤, 关吉平, 等. 集合—变分数据同化方法的发展与应用[J]. 地球科学进展, 2013, 28(6): 648-656. ] [本文引用:1] [CJCR: 1.388]
[4]	Petrie R. Localization in the Ensemble Kalman Filter[D]. London: University of Reading, 2008. [本文引用:1]
[5]	Liu Yanhua, Zhang Shuwen, Mao Lu, et al. An evaluation of simulated and estimated land surface states with two different models[J]. Advances in Earth Science, 2013, 28(8): 913-922. [刘彦华, 张述文, 毛璐, 等. 评估两类模式对陆面状态的模拟和估算[J]. 地球科学进展, 2013, 28(8): 913-922. ] [本文引用:1] [CJCR: 1.388]
[6]	Hamill T M, Whitaker J S, Snyder C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter[J]. Monthly Weather Review, 2001, 129(11): 2776-2790. [本文引用:2] [JCR: 2.758]
[7]	Anderson J L, Anderson S L. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts[J]. Monthly Weather Review, 1999, 127(12): 2741-2758. [本文引用:1] [JCR: 2.758]
[8]	Anderson J L. An ensemble adjustment Kalman filter for data assimilation[J]. Monthly Weather Review, 2001, 129(12): 2884-2903. [本文引用:1] [JCR: 2.758]
[9]	Sakov P, Bertino L. Relation between two common localisation methods for the EnKF[J]. Computational Geosciences, 2011, 15(2): 225-237. [本文引用:2] [JCR: 1.422]
[10]	Oke P R, Sakov P, Corney S P. Impacts of localisation in the EnKF and EnOI: Experiments with a small model[J]. Ocean Dynamics, 2007, 57(1): 32-45. [本文引用:1] [JCR: 1.761]
[11]	Evensen G. Data Assimilation: The Ensemble Kalman Filter (2nd)[M]. Dordrecht: Springer, 2009. [本文引用:1]
[12]	Schur I. Bemerkungen zur theorie der beschrnkten bilinearformen mit unendlich vielen vernderlichen[J]. Journal für die Reine und Angewante Mathematiek, 1911, 140: 1-28. [本文引用:1]
[13]	Burgers G, Van Leeuwen P J, Evensen G. Analysis scheme in the ensemble Kalman filter[J]. Monthly Weather Review, 1998, 126(6): 1719-1724. [本文引用:1] [JCR: 2.758]
[14]	Whitaker J S, Hamill T M. Ensemble data assimilation without perturbed observations[J]. Monthly Weather Review, 2002, 130(7): 1913-1924. [本文引用:1] [JCR: 2.758]
[15]	Sakov P, Oke P R. A deterministic formulation of the ensemble Kalman filter: An alternative to ensemble square root filters[J]. Tellus A, 2008, 60(2): 361-371. [本文引用:1]
[16]	Bishop C H, Etherton B J, Majumdar S J. Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects[J]. Monthly Weather Review, 2001, 129(3): 420-436. [本文引用:1] [JCR: 2.758]
[17]	Horn R A, Johnson C R. Matrix Analysis[M]. New York: Cambridge University Press, 1985. [本文引用:1] [JCR: 1.342]
[18]	Evensen G. Sampling strategies and square root analysis schemes for the EnKF[J]. Ocean Dynamics, 2004, 54(6): 539-560. [本文引用:1] [JCR: 1.761]
[19]	Gaspari G, Cohn S E. Construction of correlation functions in two and three dimensions[J]. Quarterly Journal of the Royal Meteorological Society, 1999, 125(554): 723-757. [本文引用:1] [JCR: 3.327]

2012

0.0

1.388

. 2012, 27(7):747-757

The research status review of data assimilation algorithm

1.Center for Earth Observation and Digital Earth, Chinese Academy of Sciences, Beijing100094, China； 2.Graduate University of the Chinese Academy of Sciences, Beijing100049, China

]In recent years, global environmental change has more and more affected the survival of human beings. In order to enhance the observation of the landatmospheric-ocean, the Global Earth Observation System of Systems (GEOSS) and Global Monitoring for Environment and Security (GMES) have been proposed. Data assimilation, the key connection between observation data and model simulations, also gets rapid development. The most significant signs are the continuous introductions of new mathematical achievements into the data assimilation fields. Under the background of the “National Airborne Remote Sensing System—The Earth Science Data Processing Software System”, we review the development of the data assimilation algorithms so as to determine the technical route and major contents of this project and promote the research on data assimilation theory and the development of the software.

近年来，全球环境变化对人类生存影响日益突出，为了加强对陆地—大气—海洋的监测，全球对地观测系统计划（GEOSS）和全球环境与安全监测计划（GMES）等相继被提出。数据同化算法作为连接观测数据与模型模拟预测的关键桥梁也得到了迅速发展，显著标志新的数学研究成果不断被引入数据同化算法中。在国家重大科技基础设施项目“航空遥感系统——地球科学数据处理软件系统”需求背景条件下，梳理遥感数据同化算法的国内外发展现状，明确数据同化算法开发的技术主线和重点内容，稳步推进数据同化算法理论研究和软件开发。

... 1 引言卡尔曼滤波(Kalman Filter,KF)是顺序同化算法的最早形式和理论基础,在线性系统和高斯白噪声下能得到无偏最优估计,但大气海洋预报模式多数是非线性系统,KF必须进行扩展才能适用^[1] ...

1994

0.0

... 1994年Evensen^[2]在海洋资料同化过程中,首次用到集合卡尔曼滤波(Ensemble Kalman Filter,EnKF) ...

2013

0.0

1.388

. 2013, 28(6):648-656

Development and application of ensemble-variational data assimilation methods

1.College of Meteorology and Oceanography,PLA University of Science and Technology, Nanjing 211101,China;2.Unit No.95903 of Airborne Troops of Air Force, Wuhan 430331, China;3. Aviation University of Air Force, Changchun 130022, China;4.Unit No.71521 of PLA, Xinxiang 453002, China

In recent years, ensemble-variational Data Assimilation (DA) methods have become cuttingedge issues of atmospheric data assimilation. The ensemblevariational DA methods which adopt the advantages of ensemble Kalman filter and variational DA is an effective way to the integration of ensemble prediction system and DA system in the Numerical Weather Prediction (NWP) system. Firstly, the concept of ensemble-variational DA is introduced after the comparison of advantages and disadvantages between variational DA and ensemble Kalman filter. Secondly, the ensemble-variational DA methods are divided into two categories by different ways of background error covariance generation. One is simple linear combination of static and ensemble covariance, and the other is augmentation of control variables. Moreover, the related development is introduced and the concept of ensemblevariational DA is expanded. Then, the application of ensemblevariational DA in the Great Britain and the U.S. is introduced. Finally, the main issues of ensemblevariational DA are reviewed and the prospect of the future development trend is listed.

近年来，集合—变分数据同化方法已成为大气数据同化领域研究的热点问题。该方法能够综合利用集合卡尔曼滤波和变分同化的优势，是实现“集合预报和数据同化一体化”的有效途径。在分析变分同化和集合卡尔曼滤波优缺点的基础上引出集合—变分数据同化的概念；按照不同实现方式，将集合—变分同化分为协方差线性组合和增加控制变量2类，介绍了相应的研究进展，并将集合—变分同化概念拓展；然后介绍了集合—变分同化在英美两国的应用；最后回顾了集合—变分同化研究的主要问题，展望了未来的发展趋势。

... 它是集合预报和KF的有效结合,利用集合来存储、传播、更新状态估计量和状态误差协方差,克服了传统KF应用中的不足,同时有效地降低了同化过程中的计算量,被广泛应用于大规模数据同化系统,并逐步与变分方法结合^[3] ...

2008

0.0

... 然而,有限个成员的集合在估计背景误差协方差矩阵时会引入伪相关^[4],即在物理上不相关或空间上距离较远的状态变量之间存在伪相关 ...

2013

0.0

1.388

. 2013, 28(8):913-922

An evaluation of simulated and estimated land surface states with two different models

Key Laboratory of Arid Climate Change and Reducing Disaster of Gansu Province, College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000, China

By using an observation system simulation experiment, the simulated soil moisture, soil temperature and surface heat fluxes are firstly compared for a period of soil drying process, respectively, from an offline Land Surface Model (LSM) and a Single Column Model (SCM) with coupled atmospheric boundary layer and LSM, and secondly, the ability of estimated land surface states are evaluated from the two models with the aid of data assimilation technique. The results show the differences of all the simulated variables are small except long-wave radiation and sensible heat fluxes being relatively large. For only the near-surface soil moisture observation assimilation, the estimated soil moisture and surface sensible heat flux with LSM are generally better than those with SCM, on the contrary, the estimated soil temperature with SCM is better, and the difference of estimated latent heat fluxes is small. However, the assimilation of both near-surface soil temperature and soil moisture observations at the same time will make the difference of heat flux estimates become large from the two models by the end of data assimilation cycle. Finally, the possible reasons for the different performances of the two models are investigated and analyzed by using the sensitivity tests. The above results imply that it should be careful when we use one-model output as another-model input, and avoid the dynamic inconsistency between the two-model states.

针对夏季土壤变干过程，利用观测系统模拟试验，比较离线的陆面模式(LSM)和耦合大气边界层的陆面模式(SCM)对土壤温度、湿度和地表热通量等陆面状态的模拟，然后借助数据同化方法，评估2类模式对陆面状态的估算能力。结果显示：2类模式除对地表长波辐射和感热通量的模拟差别较大外，对其余量则较小；只同化表层土壤湿度观测时，LSM对土壤湿度和感热通量的估算好于SCM，对土壤温度的估算则相反，而对潜热通量估算的差距很小；同时同化表层土壤温度、湿度观测会使地表热通量的估算差距增大；最后对2类模式不同表现的可能原因进行分析讨论。上述数值模拟和同化结果：当用某一类模式的模拟结果或同化产品为另一类不同模式提供初边界条件时必须注意它们之间的差异，避免出现输入量引起的模式状态量间的动力不协调现象。

... 随着同化过程的进行,背景误差协方差被系统地低估,观测数据的权重越来越小,最终完全被忽视,导致滤波发散^[5] ...

2001

2.758

0.0

... 为了减少伪相关对同化过程的影响,改善同化结果,相关学者提出了协方差膨胀和局地化2种方法^[6] ...

... ^[6,13]与背景误差协方差矩阵P^f作舒尔积,来替代原有P^f,如式(7)： ...

1999

2.758

0.0

... 协方差膨胀是由Anderson等^[7]于1999年提出的,用来修正背景误差协方差矩阵被低估的方法 ...

2001

2.758

0.0

... 这种方式会打破系统的物理平衡,不能消除远距离的伪相关^[8] ...

2011

1.422

0.0

. 2011, 15(2):225-237 DOI:10.1007/s10596-010-9202-6

Relation between two common localisation methods for the EnKF

1.Nansen Environmental and Remote Sensing Center, Thorm?hlensgate 47, Bergen, 5006 Norway

This study investigates the relation between two common localisation methods in ensemble Kalman filter (EnKF) systems: covariance localisation and local analysis. Both methods are popular in large-scale applications with the EnKF. The case of local observations with non-correlated errors is considered. Both methods are formulated in terms of tapering of ensemble anomalies, which provides a framework for their comparison. Based on analytical considerations and experimental evidence, we conclude that in practice the two methods should yield very similar results, so that the choice between them should be based on other criteria, such as numerical effectiveness and scalability.

... 虽然曾有学者研究过它们之间的关系,但他们仅仅只考虑了2种方法对单个变量的影响^[9] ...

... 来评估同化强度^[9],其表达式如下: ...

2007

1.761

0.0

. 2007, 57(1):32-45 DOI:10.1007/s10236-006-0088-8

Impacts of localisation in the EnKF and EnOI: Experiments with a small model

1.CSIRO Marine and Atmospheric Research and Wealth from Oceans Flagship Program Hobart Tasmania Australia Hobart Tasmania Australia

The performance of an inexpensive, ensemble-based optimal interpolation (EnOI) scheme that uses a stationary ensemble of model anomalies to approximate forecast error covariances, is compared with that of an ensemble Kalman filter (EnKF). The model to which the methods are applied is a pair of “perfect”, one-dimensional, linear advection equations for two related variables. While EnOI is sub-optimal, it can give results that are comparable to those of the EnKF. The computational cost of EnOI is typically about N N times less than that of EnKF, where N N is the ensemble size. We suggest that EnOI may provide a practical and cost-effective alternative to the EnKF for some applications where computational cost is a limiting factor. We demonstrate that when the ensemble size is smaller than the dimension of the model’s sub-space, both the EnKF and EnOI may require localisation around each observation to eliminate effects of sampling error and to increase the effective number of independent ensemble members used to construct an analysis. However, localisation can degrade an analysis if the length-scales of the localising function are too short. We demonstrate that, as the length-scale of the localising function is decreased, localisation can significantly compromise the model’s dynamical balances. We also find that localisation artificially amplifies high frequencies for applications of the EnKF. Based on our experiments, for applications where localisation is necessary, the length-scales of the localisation should be larger than the decorrelation length-scales of the variables being updated.

... 在EnKF中应用局地化有2个原因:空间伪相关和集合非满秩^[10,11]问题 ...

2009

0.0

... 在EnKF中应用局地化有2个原因:空间伪相关和集合非满秩^[10,11]问题 ...

1911

0.0

... 常采用舒尔积^[12],即通过一个基于距离的相关系数矩阵#cod#x003c1 ...

1998

2.758

0.0

... ^[6,13]与背景误差协方差矩阵P^f作舒尔积,来替代原有P^f,如式(7)： ...

2002

2.758

0.0

... CL只适用以下方案,如：传统EnKF、EnSRF(Ensemble Square Root Filter,EnSRF)^[14]、DEnKF(Deterministic Ensemble Kalman Filter,DEnKF)^[15],而不适用于ETKF(Ensemble Transform Kalman Filter,ETKF)^[16] ...

2008

0.0

2001

2.758

0.0

1985

1.342

0.0

... 由矩阵求逆引理^[17],得到T,如公式(18): ...

2004

1.761

0.0

. 2004, 54(6):539-560 DOI:10.1007/s10236-004-0099-2

Sampling strategies and square root analysis schemes for the EnKF

1.Hydro Research Centre, Bergen Norway, and Nansen Environmental and Remote Sensing Center Bergen Norway

The purpose of this paper is to examine how different sampling strategies and implementations of the analysis scheme influence the quality of the results in the EnKF. It is shown that by selecting the initial ensemble, the model noise and the measurement perturbations wisely, it is possible to achieve a significant improvement in the EnKF results, using the same number of members in the ensemble. The results are also compared with a square root implementation of the EnKF analysis scheme where the analyzed ensemble is computed without the perturbation of measurements. It is shown that the measurement perturbations introduce sampling errors which can be reduced using improved sampling schemes in the standard EnKF or fully eliminated when the square root analysis algorithm is used. Further, a new computationally efficient square root algorithm is proposed which allows for the use of a low-rank representation of the measurement error covariance matrix. It is shown that this algorithm in fact solves the full problem at a low cost without introducing any new approximations.

... 1 线性平流模型线性平流(Linear Advection,LA)模型^[18]具有一维周期性,状态向量X维度为n,如下: ...

1999

3.327

0.0

... 局地裁剪函数是由高斯和科恩于1999年提出的^[19],其表达式如下： ...