近地表速度建模研究现状及发展趋势

引用本文

王振宇, 杨勤勇, 李振春, 胡光辉, 尹力, 王杰. 近地表速度建模研究现状及发展趋势. 地球科学进展, 29(10): 1138-1148
Wang Zhenyu, Yang Qinyong, Li Zhenchun, Hu Guanghui, Yin Li, Wang Jie. Research Status and Development Trend of Near-Surface Velocity Modeling. Advances in Earth Science, 29(10): 1138-1148 复制到剪切板

Permissions

This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

近地表速度建模研究现状及发展趋势

王振宇^1,², 杨勤勇¹, 李振春², 胡光辉¹, 尹力^1,², 王杰¹

1.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103

2.中国石油大学(华东)地球科学与技术学院,山东青岛 266580

摘要

速度是反映地下构造和岩石物性的一个重要参数。近地表速度的精度直接影响勘探区域的地震资料静校正、速度分析以及最终成像的效果。目前常用的近地表建模方法和技术多基于高频近似的射线理论,不能满足当前近地表精细建模的需求。通过对微测井、折射波法、面波法、走时层析以及全波形反演等近地表建模技术的全面调研,总结了它们的适应性、优缺点及研究应用现状,指出联合走时层析与波形反演的技术方法在时间域分步骤、多尺度的反演策略是近地表高精度建模的有效手段和发展方向,能有效提高建模精度,适应高精度成像要求。该方法在近地表的矿产普查、工程物探、油气勘探等领域存在广泛的应用前景。

关键词: 走时层析; 全波形反演; 多尺度; 联合反演策略; 高精度

中图分类号:P631 文献标志码:A 文章编号:1001-8166(2014)10-1138-11

Research Status and Development Trend of Near-Surface Velocity Modeling

Wang Zhenyu^1,², Yang Qinyong¹, Li Zhenchun², Hu Guanghui¹, Yin Li^1,², Wang Jie¹

1.Sinopec Geophysical Research Institute, Nanjing 211103, China

2.School of Geosciences, China University of Petroleum, Qingdao 266580, China

Abstract

Seismic velocity is a critical factor in reflecting underground structure and lithology. The accuracy of near-surface velocity directly influences the results of static correction, velocity analysis and the final imaging in exploration areas. Near-surface modeling methods and technologies commonly used are based on the ray theory of high-frequency approximation, which barely meet the highaccuracy request in current nearsurface modeling. Through an overall investigation into nearsurface modeling technologies such as micro logging, mini refraction, surface wave method, traveltime tomography and Full Waveform Inversion (FWI), this paper summarizes their adaptability, advantages and disadvantages, research and application status, points out that by combining traveltime tomography and waveform inversion, the step-by-step and multiscale inversion strategy in the time domain is an effective means and trend of near-surface high-accuracy modeling, which can improve modeling accuracy effectively and meet the requirements of high accuracy imaging. Thus, the method has widespread application prospects in near-surface mineral prospecting, engineering geophysics and hydrocarbon exploration.

Keyword: Traveltime tomography; Full waveform inversion; Multiscale; Joint inversion strategy; High-accuracy.

Show Figures

1 引言

随着世界经济对油气、地下水^[1]、矿产等资源需求量的日益增加, 勘探力度逐步加大, 这就对高精度建模成像技术提出了更高的要求。而中国陆相沉积特点, 近地表地质条件具有地表和地下的“ 双复杂” 特性。复杂地表表现为近地表结构不连续、地形起伏大、低降速层(速度/厚度)变化大、灰岩出露/岩性变化大、潜水面埋深/高速层顶面变化大等; 地下复杂表现为目的层产状不连续、逆掩推覆、高陡构造等; 地下复杂储层拥有礁滩、缝洞、致密砂岩、裂隙等不同储层类型。图1描述了近地表地震地质条件的复杂性。

	Figure Option View Download New Window
	图1 复杂近地表概况Fig 1 Complicated near surface general situation

这些复杂的地震地质条件给地震勘探带来了严峻的挑战, 具体表现为：①干扰波发育, 单炮资料信噪比低; ②静校正问题突出, 地震波初至扭曲严重; ③去噪与弱反射波信号提取难, 速度分析困难; ④波场复杂, 成像精度低等。复杂的近地表条件导致近地表速度建模精度不高, 严重影响到勘探区域的地震资料静校正、速度分析以及最终的成像结果, 进一步影响解释人员确定低缓冲构造及地层塌陷, 确定水平井的定位, 识别精细油藏构造。因此, 如何提高近地表速度模型精度将是复杂地表成像处理的关键问题^[2], 近地表速度模型的精确重建对近地表的矿产普查, 工程物探^[3]以及改善近地表复杂区老油田成像精度, 提高油气产量具有重要意义。

本文通过对传统近地表速度建模, 全波形反演技术研究进展与应用现状的全面调研, 指出联合走时层析与波形反演策略, 在时间域分步骤、多尺度反演是近地表高精度建模的有效手段及发展方向。

2 近地表速度建模方法

在山地、黄土塬^[4]等复杂地质构造区域, 浅表层干扰波强烈, 吸收衰减严重、高速岩层出露以及近地表横向速度变化剧烈, 使地震波的传播路径变得非常复杂, 同时野外施工困难, 导致采集到的地震资料信噪比低, 道间时差变化剧烈^[5], 表层结构调查工作越来越受到人们的重视, 出现了很多近地表速度反演方法, 如微测井、折射波法、面波法以及走时层析方法等, 这几种方法在实际生产中应用比较广泛^[6]。

2.1 微测井

微测井是在一口或多口穿过低、降速带的井中, 采用井中激发、地面接收, 地面激发、井中接收或井中激发、井中接收等方式, 利用多次激发而得到的透射波时距曲线的拐点和折射段的斜率来划分低速层、降速层速度和厚度^[7]。

微测井法能够较准确地确定测点处表层速度随深度变化的规律, 但在低速带厚度和速度变化比较大的地区, 必须加密测点。利用微测井法调查的表层结构一般比较准确, 特别是对于低降速层较厚, 速度变化较大的表层结构, 其计算精度要优于其他方法, 该方法基本不受地表条件的限制, 适用范围较广^[8], 但这种方法成本高、效率低, 一般仅用于表层结构调查的控制点测量。

2.2 小折射法

小折射法是根据折射波基本理论, 通过直达波和折射波时距曲线计算出近地表各层的厚度和埋深。

表层调查应用小折射并用稀疏的微测井和推水坑加以校正, 在高速层埋藏较深时, 一般采用移动炮点进行观测, 应用首尾拼接的折射波时距曲线进行解释, 得到该点的表层结构。该方法的优势在于操作简单、成本低、效率高, 是一种常用的表层结构调查方法。因此该方法适用于地表平缓、表层结构简单且低降速层变化较小的区域^[8]。段云卿等^[9]进行了三分量的小折射的表层研究。利用小折射法获得的低降速层厚度一般偏小, 只有在折射界面稳定的情况下, 计算精度较高; 在低降速层厚度较大、速度变化较大时, 计算精度略低。由于小折射法使用的是偏移距较小的初至折射波, 对地形起伏剧烈, 以及表层速度变化大的地区不适用。

2.3 面波法

面波勘探多指瑞雷波勘探。在反射地震勘探中, 面波通常都被作为干扰波剔除。由于面波包含了许多有用地下介质信息, 并且有时比其他方法更容易得到这些有用信息, 因此面波勘探被广泛应用于地表及地质条件复杂的非沙漠区及沙漠区近地表地质调查。这是因为面波勘探具有2个特征：一是在层状介质中传播时所特有的频散特性, 其传播相速度和穿透深度随频率和波长的改变而改变, 即不同频率(波长)面波的传播特性反映了地层垂向上的变化, 同一频率(波长)面波的传播特性反映了地质条件横向上的变化。换言之, 面波勘探实质是频率勘探, 面波的频散特性是其探测浅层地质结构的理论基础。二是同一介质中面波相速度与横波速度具有相关性。据此可以将所测地层的面波速度转换为横波波速。面波法求取横波速度较其他一些方法(如测井、折射法地震勘探等)具有效率高、精度高等优点。张维等^[10]在玉溪和夏垫两地分别开展了天然源和人工源面波联合勘探试验, 利用采集到的人工源和天然源面波信息进行数据处理并提取频散曲线, 反演浅部地层的横波速度结构, 大大提升了面波勘探能力, 但在数据采集和处理技术上还存在诸多问题。常规面波勘探方法探测深度相对较浅, 最深不过50~60m, 其理论研究以及实际应用有待进一步的深入。

2.4 层析反演方法

层析成像最先用于医学, 20世纪80年代地震层析成像进入地球物理领域, 由于走时层析成像效率高, 稳健, 实际应用费用低廉, 一直是研究热点之一, 走时层析通过最小化观测旅行时与计算旅行时之间的差值来计算速度扰动, 更新速度场, 层析线性方程可以表达为^[11]：

L∆s=∆t, (1)

式中：L是灵敏度矩阵,其元素为射线在网格内的射线路径长度;∆t为走时残差向量; ∆s是反演的慢度更新量,通过不断迭代更新速度模型。

射线追踪是走时层析的核心技术^[12], 桑运云^[13]推导了抛物旅行时插值射线追踪公式, 提出了基于抛物旅行时插值的最短路径射线追踪方法, 克服了最短路径方法中射线“ 之” 字路径的缺陷, 提高建模精度。Zhou^[14]引入多尺度层析来处理不均匀的射线覆盖, 减少层析中的多解性问题, 并对南加利福尼亚地壳结构进行了三维测试, 验证了利用多尺度层析比传统的单尺度层析能够得到分辨率更高的速度模型。随后, Liu等^[15]展示了在实际资料中常见的上覆地层速度高于下覆地层速度的Yilmaz速度模型对初至走时层析射线路径、静校正的严重影响, 将多尺度可变层层析(Multiscale Deformable-Layer Tomography, DLT)应用到该模型中显著的提高了静校正结果和深层成像精度。Taillandier^[16]采用伴随状态法避免Fré chet矩阵导数估计, 对于大数据体在提高计算效率的同时, 对近地表速度异常有很好的刻画能力。

旅行时层析对于反演地下速度结构是一个很稳健的工具, 尽管这种方法是快速有效的, 但是它是基于高频近似, 而地震震源是有限频带的, 同时它仅利用初至旅行时, 忽略了地震记录中包含在振幅中其他重要的信息。因此, 基于这种本身技术的局限性, 存在建模的“ 盲区” , 旅行时层析反演出来的速度模型是次优的, 在分辨率和精度上不能满足实际资料处理的需要。

为了克服走时层析成像的高频局限, 近年来, 地震勘探工作者做出了很多努力, 产生了波路径 ^[17~21]和菲涅耳体层析方法^[22~23]。菲涅耳体走时层析虽然与波动方程走时反演的效果相当, 但与射线走时层析一样需要进行高频近似, 且比射线方法更为耗时。

3 全波形反演

全波形反演是当今的研究热点, 它基于Bayes理论框架之下, 利用叠前地震波场的运动学和动力学信息重建地下物理模型参数, 在理论上被认为是建模精度最高的手段, 对复杂构造较小储层等具有精细刻画的潜力^{[24, 25]}。全波形反演是一个观测数据与计算数据的拟合过程^[26], 在数学上是一个高度病态的非线性问题, 涉及模型参数化、误差泛函的建立、数据预处理、波场的数值模拟, 子波估计等研究内容^[27]。从20世纪80年代Lailly^[28]和Tarantola^[24]分别提出时间域的全波形反演, 由于时间域同时反演所有频率成分, 使得问题的非线性问题增大, Bunks^[29]提出了时间域的多尺度反演, 通过对资料处理分解为不同的空间尺度, 从而增加了问题的稳定性, 降低了非线性程度。90年代, Pratt^{[30, 31]}提出了频率域全波形反演, 从低频逐步走向高频的策略极大程度的降低了非线性。在梯度求取中采用伴随状态法^[32]通过震源正传波场和残差回传波场相关求取梯度, 避开了对Fré chet矩阵求导, 使梯度计算变得更加高效、方便, 极大地推动了全波形反演的实用化进程。

20世纪80年代, Gauthier^[33]等和Mora^[34]实现了二维地震资料全波形反演。随着计算机水平的提高, 三维全波形反演在90年代中后期陆续出现^{[35, 36]}, 2010年, Sirgue等^[37]率先对挪威北海油田OBC数据实现了全波形反演, 对浅层气云进行了准确描述, 并对周边充气的断裂构造进行了精细的刻画, 发展了直接对高精度速度体进行地震资料解释的新思路。随后, 全波形反演海上三维实际资料应用陆续出现^{[38, 39]}。在缺少低频的情况下, Shin^[40]采用拉普拉斯域联合频率域全波形反演, 首先利用拉普拉斯域全波形反演对频率不敏感的特性来恢复长波长分量, 继而以此为初始模型利用频率域全波形反演恢复短波长分量实现高精度建模。

2012年, 壳牌公司和东方地球物理公司合作实现了二维陆上资料的全波形反演^[41]。但是这一研究是基于低频大偏移距的特殊的观测系统, 这在常规实际资料中是难以实现的, 在地震采集中也难以大规模实施。针对国内陆上探区特点, Hu^[42]开展了面向目标层的全波形反演研究, 结果展示了全波形反演对浅中层建模的积极作用, 成像剖面有很大改善, 构造与测井信息更加吻合。

然而, 由于数据空间向参数空间映射强烈的非线关系性以及地下地质模型的复杂性和地震传播过程的正演算子的复杂性, 全波形反演陆上实用化是非常困难的。胡光辉^[43]通过模型验证分析了全波形反演陆上实际资料应用的困难。杨勤勇^[44]指出陆上全波形反演的应用瓶颈在于：①路上地震资料常规三维勘探中采用滚动采集以及观测系统设计多基于反射波勘探, 偏移距较小难以满足全波形反演所要求的全方位角、大偏移距观测系统; ②低频信息缺失; ③陆上数据预处理面临的挑战; ④陆上炸药震源, 随机干扰严重。

全波形反演是一套完美的数学理论体系, 已逐渐从模型试算走向实际资料应用。而经典的全波形反演实用化是非常困难的, 它要求准确的背景速度场以及低频、大偏移距信息, 常规观测系统难以满足。全波形反演不仅利用深层反射波, 折射波, 同时还利用直达波, 浅层折射波等近地表波场, 对浅中层也具有精确刻画能力, 但目前对这方面的研究很少。通过分频带, 多尺度的多种手段联合反演来大幅度提高速度估计和成像精度是一种新的近地表反演流程。

4 分步骤、多尺度联合反演策略

鉴于常规的初至走时层析技术方法本身具有局限性, 仅利用地震波运动学特征精确度不高, 存在建模的“ 盲区” , 再加上人工拾取初至波存在较大误差, 工作量大。而全波形反演技术应用受到地震资料的种种限制, 要求准确的背景速度场以及低频、大偏移距信息, 使其在实际资料应用中遇到了很多困难, 还不能完全达到实用化的目的。Sheng^[45]联合初至走时层析与波形反演利用近地表折射数据进行最早波至波形层析(Early arrival waveform tomography), 利用初至波反演近地表低波数背景速度场、在L2范数约束的最早波至波形反演反演高波数扰动速度场。这一技术基于波动方程不仅充分运用运动学和动力学特征, 还可以避开全波形反演大偏移距和低频信息的限制及人工拾取初至波步骤, 完成高精度近地表建模及校正。模型试验结果表明其结果较走时层析更加精确, 收敛性更好。对于墨西哥湾海洋数据, 由浅层低速气团引起的静校正问题突出, 在利用该方法得到的速度模型经过静校正之后比走时层析效果有了很大的提高, 对Mapleton Utah 陆地数据反演结果比走时层析结果能够更好地与测井曲线匹配。

4.1 基本原理：

以二维声波方程为例, 在时间域采用空间四阶时间二阶交错网格有限差分方法正演^[46], 模型顶边界应用自由表面边界, 其他边界利用完全匹配层(Perfectly Matched Layer, PML)边界^[4750]。

目标函数采用数据残差L2范数, 通过最小化匹配函数不断更新速度模型:

$\begin{matrix} E = \frac{1}{2} \sum_{s} \sum_{g} \int (δp (r_{g}, t | r_{s} {))}^{2} dt (2) \end{matrix}$

数据残差表示为:

$\begin{matrix} δp (r_{g}, t | r_{s}) = p_{obs} (r_{g}, t | r_{s}) - p_{cal} (r_{g}, t | r_{s}) \end{matrix}$ (3)

式中: $\begin{matrix} p_{obs} (r_{g}, t | r_{s}) \end{matrix}$ 和 $\begin{matrix} p_{cal} (r_{g}, t | r_{s}) \end{matrix}$ 分别为观测数据和计算数据。反演策略基于Tarantola提出的伴随方法, 在最小化目标范数时利用非线性预处理的共轭梯度法^[20], 通过正传波场和反传波场残差零延迟互相关来计算目标函数对于速度的梯度^{[24, 51, 52]}。

$\begin{matrix} g (r) = \frac{2}{c (r)} \sum_{s} \int \overset{\cdot}{p} (r, t | r_{s}) \overset{\cdot}{p}' (r, t | r_{s}) dt (4) \end{matrix}$

式中: $\begin{matrix} \overset{\cdot}{p} \end{matrix}$ 表示 $\begin{matrix} p \end{matrix}$ 的时间导数, $\begin{matrix} p (r, t | r_{s}) \end{matrix}$ 表示正传波场, $\begin{matrix} p' (r, t | r_{s}) \end{matrix}$ 表示反传波场残差, 速度模型c(r)沿共轭方向不断更新迭代:

$\begin{matrix} d_{k} = - P_{k} g_{k} + β_{k} d_{k - 1} (5) \end{matrix}$

$\begin{matrix} k = 1, 2, \dots, k_{\max} \end{matrix}$ 表示迭代次数, $\begin{matrix} g = g (r) \end{matrix}$ 是速度模型的所有成像点, $\begin{matrix} P \end{matrix}$ 是常规的几何扩散预处理因子^[53]。

利用Polak-Ribié re formula公式来求取参数 $\begin{matrix} {β_{k}}^{[54]} \end{matrix}$ :

$\begin{matrix} β_{k} = \frac{{g^{T}}_{k} \cdot (P_{k} g_{k} - P_{k - 1} g_{k - 1})}{{g^{T}}_{k - 1} \cdot P_{k - 1} g_{k - 1}} (6) \end{matrix}$

速度模型通过下式来更新:

$\begin{matrix} c_{k + 1} (r) = c_{k} (r) + λ_{k} d_{k} (r) (7) \end{matrix}$

式中: $\begin{matrix} λ_{k} \end{matrix}$ 是步长, 由二次线性搜索方法确定^[54]; $\begin{matrix} d_{k} (r) \end{matrix}$ 是共轭方向矢量。每一次迭代, 利用一次正演和一次反投影来计算梯度方向, 初始模型 $\begin{matrix} c_{0} (r) \end{matrix}$ 是旅行时层析结果^[55]。Hanafy等^[56]利用最早波至波形反演方法, 基于可控震源激发, 最大偏移距232 m的观测系统在Wadi Qudaid开展了探测地下水储藏潜力的研究, 合成数据和实际资料结果表明最早波至波形反演比初至走时层析能更加精细地刻画地下速度结构, 并指出用最早波至波形反演方法可以提高18%的储藏潜力, 展现了巨大的经济效益。

Sheng等^[45]提出的最早至波形层析的新方法(Early-arrival Waveform Tomography, EWT), 通过对地震数据加窗仅仅反演最早至波场。与传统的全波形反演相比, 由于需要更少的数据匹配, 降低了非线性, 但是反演中的高频数据使目标函数仍然具有高度的非线性, EWT还是会遇到局部极小问题。Bunks等^[29]提出时间域多尺度波形层析, 利用Hamming-window 滤波器对地震子波和地震数据进行低通滤波, 使反演从低频到高频数据依次进行。由于对于慢度的目标函数在低频比在高频更加线性, 多尺度波形层析(Mutiscale Waveform Tomography, MWT)更容易达到局部极小。而Bunks等^[29]利用Hamming-window function进行低通滤波对于时间域MWT不是最有效的滤波器。而且在反演过程中, 频带选择是任意的。对于每一个频带, 反演进行多次迭代, 这就导致过多的频带花费大量的计算时间。在频率域, Sirgue等^[57]提出了一种最优频带选择策略, 极大地减少了波形反演的计算量, 把这种方法应用到时间域, 2009年, Chaiwoot Boonyasiriwats结合Bunks等提出的多尺度层析以及Sirgue等在频率域提出的最优频带选择策略将Sheng等的方法推进一步, 不再是仅仅利用折射数据, 而利用全波场信息, 通过滤波并选择最优频带在时间域运用分频带和变化网格相结合的方法来克服波形反演中的严重局部极小值问题, 分步骤、分尺度的联合初至走时层析和全波形反演进行近地表速度建模, 提高了收敛速度和计算效率, 精确地恢复了速度模型的低波数成分和高波数成分^[58~60]。

4.2 对于MWT的有效的低通滤波

传统的时间域波形层析^[45]只利用一个频带数据和一种有限差分网格容易导致局部极小问题。通过利用几个频带数据和变化网格大小, 多尺度方法^[29]成功的反演了复杂的Marmousi 模型。在时间域进行多尺度反演, 低通滤波是非常关键的。

Bunks^[29]利用Hamming-windowfunction^[61]对震源子波和数据进行低通滤波。震源子波在反演之前已经被估计得到^[62~65]。维纳滤波器一般应用在频率域, 它的一个优点是把一个信号滤到接近另一个目标信号。低通维纳滤波可以通过下式计算:

$\begin{matrix} f_{Wiener} (ω) = \frac{W_{target} (ω) W_{original}^{†} (ω)}{{|W_{original} (ω)|}^{2} + ε^{2}} (8) \end{matrix}$

式中:f_Wiener是维纳滤波器, W_original是初始子波, W_target(ω )是低频目标子波, $\begin{matrix} ω \end{matrix}$ 是角频率, $\begin{matrix} ε \end{matrix}$ 是一个小参数阻止数值溢出, $\begin{matrix} † \end{matrix}$ 代表复共轭, 滤波的主要目的是得到一个最小谱泄露的低频带子波。

在时间域MWT, 通过对子波和数据进行维纳滤波使得滤过的震源子波和数据基本有同样的频带变化范围。

4.3 最优频带选择策略

Sirgue 等^[57]提出的在频率域波形反演中选择最优频带范围策略被延伸到时间域来减少恢复的速度结构中的波数冗余。单一频率中, 一个炮检对的贡献仅仅是一个波数成分。速度模型中一系列的垂直波数成分可以通过一系列炮检对来更新。

Sirgue等^[57]提出的选择频带公式是:

$\begin{matrix} f_{n + 1} = \frac{f_{n}}{α_{\min}} (9) \end{matrix}$

式中: $\begin{matrix} f_{n} \end{matrix}$ 是当前频率, $\begin{matrix} f_{n + 1} \end{matrix}$ 是下一个将要选择的频率, α _min=z/ $\begin{matrix} \sqrt[]{h^{2} + z^{2}} \end{matrix}$ 是依赖最大半偏移距 $\begin{matrix} h \end{matrix}$ 和最大成像深度 $\begin{matrix} z \end{matrix}$ 的参数。

在时域反演, 一个给定带宽多个频率同时使用, 在这里使用频带最大振幅谱一半的频率来确定频带的最小和最大频率, 用于计算恢复的波数范围, 振幅小于最大振幅一半的频率成分被认为对恢复波数微不足道。尽管如此, 来自这些频率成分的贡献可以当做来自2个连续频带恢复的的两个波数范围的重叠区域。

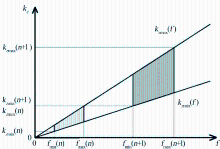	Figure Option View Download New Window
	图2 时间域波形层析最优频带选择策略^[58]Fig 2 Strategy for choosing optimal frequency bands for time-domain wave form tomography^[58]

图2为时间域波形层析最优频带选择策略示意图, 在第n个频带, 频带最小和最大频率分别为 $\begin{matrix} f_{\min} (n), f_{\max} (n) \end{matrix}$ , 决定了波数范围:

$\begin{matrix} \begin{matrix} k_{zmin} (n) = \frac{4 π f_{\min} (n) α_{\min}}{c_{0}} (10) \\ k_{zmax} (n) = \frac{4 π f_{\max} (n)}{c_{0}} (11) \end{matrix} \end{matrix}$

对于下一个频带 $\begin{matrix} n + 1 \end{matrix}$ , 将要更新的最低波数等于当前频带 $\begin{matrix} n \end{matrix}$ 的最高波数:

$\begin{matrix} k_{zmin} (n + 1) = k_{zmax} (n) (12) \end{matrix}$

其中, 起始频率选择是任意的。一个好的起始频带取决于模型的复杂性。在实际数据中, 一个合理的准则是利用带有最低峰值频率的频带作为初始频带。

4.4 模型测试

图3d真实速度模型是由多个小尺度的速度异常体嵌入变化缓慢的背景速度场的2d模型, 201炮和201个检波器沿地表均匀分布, 间隔20 m, 最大偏移距4km, 这些小尺度的异常体利用传统的旅行时层析是很难恢复的。

单尺度波形反演(Single-scale Waveform Tomography, SWT)^[43]和多尺度波形反演(Multiscale Waveform Tomography, MWT)应用到这个数据集。SWT中, 反演利用初始的震源和数据; MWT中, 利用震源和数据的多个频带。通过频带选择策略, 仅仅利用5和20Hz的雷克子波频带。对于低频带, 使用20 m的网格, 2ms的时间采样间隔, 不会有数值频散和不稳定性的危险。对于高频带, 使用5米的网格, 0.5ms时间采样间隔。SWT和MWT的初始速度模型都利用走时层析结果。

Figure Option
View Download New Window

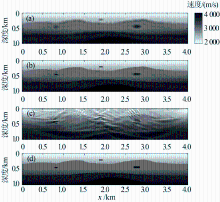图3 时间域多尺度波形反演结果(a)5Hz峰值频率数据MWT结果; (b)5Hz和20Hz峰值频率数据MWT反演结果; (c)20Hz峰值频率数据SWT反演结果; (d)真实速度模型^[58]Fig 3 Time-domain multiscale waveform inversion results(a)MWT velocity tomogram obtained after inversion using 5-Hz peak-frequency data; (b)MWT velocity tomogram obtained after inversions using 5- and 20-Hz peak-frequency data; (c)SWT velocity tomogram obtained after inversion using 20-Hz peak-frequency data; (d)the true velocity model^[58]

图3中SWT的最终模型结果展示了局部极小值问题的影响, 恢复模型远不如使用MWT得到的模型。而且, SWT的总运行时间23小时, 比MWT长64%, 残差曲线表明MWT残差比SWT残差低16%。将层析结果和真实模型对比表明MWT收敛到局部极小而SWT没有。通过将MWT成功应用到2D模型, 并与传统单尺度波形反演结果对比, 可以看出MWT有更高的计算效率, 更快的收敛速度。通过使用维纳滤波和最优频带选择策略提高了计算效率。通过应用最优频带选择策略, 利用更少的频带, 避免了不必要的计算成本。在低频段, 利用较大网格和时间步长, 正演模拟和反演是高效的。通过逐步的恢复速度结构的高波数成分, 从低到高, 多尺度方法可以提高波形层析的收敛性质并在一定程度上克服误差泛函中遭遇的局部极小问题。模型实验表明, 对于传统的时间域波形反演, 多尺度方法可以提高计算效率和收敛速度。

4.5 海上实际资料应用

将该方法应用到墨西哥湾海上实际资料。在反演之前, 为了进行3D几何扩散校正, 通过在频率域滤波将数据从3D变化到2D^[51], 数据中初至前的噪声被切除, 通过谱比法^[66]估计衰减因子Q, 并利用反Q滤波器^[67]对数据进行补偿, 沿着海底反射叠加来估计子波。数据通过低通滤波分为两个频带0~15Hz和0~25Hz。利用走时层析提供初始数据依次反演。反演由三部分组成, 每一部分利用不同时间长度的切割时窗对数据切割截取。第一部分将滤波后的数据利用1s的切割时窗截取, 依次对0~15Hz和0~25Hz的数据进行反演, 对由第一部分重建的的速度模型作为第二部分的初始模型, 其中第二部分切割窗口长度2s, 第三部分, 切割窗口长度3s。图4展示了波形反演结果, 比初始模型走时层析结果有更高的分辨率。

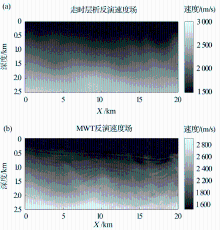	Figure Option View Download New Window
	图4 墨西哥湾海洋数据反演结果(a)走时层析反演结果; (b)MWT反演结果^[59]Fig 4 Inversion results from the marine data(a)The initial velocity model obtained from traveltime tomography; (b)The velocity tomogram obtained from waveform tomography^[59]

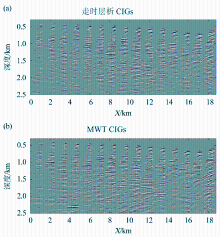
图5a, b分别是走时层析和波形反演偏移成像结果。图6是图5中方框内的偏移成像放大结果。采用波形反演结果作为偏移速度, 偏移成像比走时层析结果作为偏移速度得到的偏移成像更加聚焦。图7中通过对比二者共成像点道集的拉平程度可以看到波形反演结果比走时层析结果更加精确。

一些专业公司在近地表建模方面做了很多工作, PGS公司^[68]在北海(North Sea)利用折射波和回折波的特征波全波形反演对浅水地质环境进行速度建模, 反演得到高分辨率速度模型, 小尺度异常体得到了精确刻画, 偏移成像和共成像点道集均展现出了其优于反射层析结果。沙特阿拉伯石油公司和GeoTomo ^[69]公司将最早至波形反演应用到Saudi Arabia的三维陆上地震数据, 结果显示比走时层析结果提高了喀斯特地形特征的纵横向分辨率, 并反演得到走时层析所未反演出的高速层。

在实际资料应用中, 预处理环节是至关重要的, 其中涉及到子波估计、吸收衰减补偿, 几何扩散校正, 消除噪音等, 其他一些额外的处理策略也是必不可少的。

另一方面, 王华忠等^[25]分析指出需要合理的增加相位信息在泛函中的比例, 综合应用波场中旅行时、相位和振幅的信息。通过修改目标函数来降低非线性问题, 董良国等^[70]分析了不同目标函数随不同物性参数的不同扰动尺度的变化性态, Shen^[71]通过加入更多的相位信息修改目标函数, 降低波形, 振幅的敏感性, 减少非线性程度, 对传统的L2范数波形反演实用化具有更进一步的推动作用。此外, 该方法结合面波勘探^[72]以及其他非地震方法如高精度重力法^[73], 浅层电磁法^[74~75]及电阻率法进行近地表高精度速度建模具有广泛的应用前景。

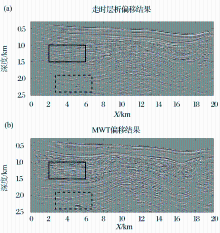	Figure Option View Download New Window
	图5 墨西哥湾海洋数据偏移结果(a)走时层析偏移结果; (b)MWT偏移结果^[59]Fig 5 Migration images from the marine data.(a)The Kirchhoff migration image obtained using the original data and the traveltime tomogram; (b)The Kirchhoff migration image obtained using the waveform tomogram^[59]

Figure Option
View Download New Window

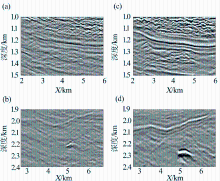图6 偏移成像放大结果对比(a)和b)分别是图5a实线框和虚线框放大结果; (c)和(d)分别是图5b实线框和虚线框放大结果^[59]Fig 6 Zoomed views of migration images from the marine data.Using the traveltime tomogram, the Kirchhoff migration images in(a)the solid box and(b)the dashed box are obtained. Using the waveform tomogram, the Kirchhoff migration image in(c)the solid box and(d)the dashed box are obtained^[59]

	Figure Option View Download New Window
	图7 共成像点道集(CIGs)对比 ^[59](a)走时层析结果CIGs; (b)MWT结果CIGsFig 7 Common image gathers (CIGs) obtained from the marine data migrated(a)traveltime tomogram; (b)waveform tomogram as the velocity model^[59]

5 结论与展望

我国西部山前带、沙漠、黄土塬等地区近地表条件复杂, 地表高程变化大、横向速度变化剧烈, 低降速带发育, 近地表速度建模十分困难。本文通过对传统近地表建模技术的全面调研, 指出了它们的优缺点及适应性, 总结了基于射线类反演的理论建模盲区以及全波形反演(FWI)的应用瓶颈。这些方法, 很难做到近地表的高精度建模, 而近地表速度模型的精度直接影响速度分析精度以及最终成像的效果, 尤其是当前由构造型油气藏到岩性油气藏的勘探目标的转变, 高精度的近地表建模显得尤为重要。近年来提出的最早波至波形反演联合走时层析是实现近地表高精度建模的有效手段及未来发展方向。该方法基于射线类走时反演建立初始模型, 通过最早波至波形反演, 利用特征波的动力学特征, 可有效的解决近地表复杂区的高精度建模问题, 进而提高近地表复杂区的整体速度建模精度, 改善这些区块的成像质量。对近地表复杂区的老油田资料进行二次处理, 改善其建模成像精度, 探明新的隐蔽型油气藏, 提高老油区的油气产量具有重要意义。与此同时, 该方法与其他非地震方法的结合在近地表的矿产普查, 工程物探, 油气勘探等领域具有广泛的应用前景。

致谢

感谢中石化“ 近地表复杂区早至波全波反演建模技术研究” 项目组的支持, 感谢SEISCOPE研究组专家学者的有益讨论。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Jia Yongfeng, Guo Huaming. Hot topics and trends in the study of high arsenic groundwater[J]. Advances in Earth Science, 2013, 28(1): 51-61. [贾永锋, 郭华明. 高砷地下水研究的热点及发展趋势[J]. 地球科学进展, 2013, 28(1): 51-61. ] [本文引用:1] [CJCR: 1.388]
[2]	Wang Huazhong, Liu Shaoyong, Yang Qinyong, et al. Seismic exploration strategy and inmage processing in mountain areas[J]. Oil Geophysical Prospecting, 2013, 48(1): 151-159. [王华忠, 刘少勇, 杨勤勇, 等. 山前带地震勘探策略与成像处理方法[J]. 石油地球物理勘探, 2013, 48(1): 151-159. ] [本文引用:1] [CJCR: 1.333]
[3]	Ma Wei, Niu Fujun, Mu Yanhu. Basic research on the major permafrost projects in the Qinghai-Tibet Plateau[J]. Advances in Earth Science, 2012, 27(11): 1185-1191. [马巍, 牛富俊, 穆彦虎. 青藏高原重大冻土工程的基础研究[J]. 地球科学进展, 2012, 27(11): 1185-1191. ] [本文引用:1] [CJCR: 1.388]
[4]	Qin Ning, Li Zhenchun, Sang Yunyun, et al. The research of travel time tomographic velocity modeling method on first break[J]. Progressin Geophysics, 2014, 29(1): 255-260. [秦宁, 李振春, 桑运云, 等. 初至波走时层析速度建模方法研究[J]. 地球物理学进展, 2014, 29(1): 255-260. ] [本文引用:1]
[5]	Cheng Jianyuan, Li Ning, Hou Shining, et al. Development status overview of seismic prospecting technology in loess tableland [J]. Coal Geology of China, 2009, 21(12): 72-76. [程建远, 李宁, 侯世宁, 等. 黄土塬区地震勘探技术发展现状综述[J]. 中国煤炭地质, 2009, 21(12): 72-76. ] [本文引用:1] [CJCR: 0.6955]
[6]	Pan Yanmei, Liu Yuzhu, Yang Kai. Preliminary study on velocity modeling for irregular surface[J]. Xinjiang Petroleum Geology, 2009, 30(4): 523-525. [潘艳梅, 刘玉柱, 杨锴. 起伏地表速度建模初步研究[J]. 新疆石油地质, 2009, 30(4): 523-525. ] [本文引用:1] [CJCR: 0.55]
[7]	Li Minghai. Application of uphole methods in the inwestigation of near surface structure[J]. Progress in Exploration Geophysics, 2008, 31(5): 378-382. [李明海. 地面微测井在山地表层结构调查中的应用[J]. 勘探地球物理进展, 2008, 31(5): 378-382. ] [本文引用:1]
[8]	Chen Wujin, Zhang Zhilin, Zhu Yong, et al. Discussion on integrative near-surface method in Yongxin area[J]. Oil Geophysical Prospecting, 2008, 43(Suppl. 2): 70-73. [陈吴金, 张志林, 朱勇, 等. 永新地区综合表层调查方法探讨[J]. 石油地球物理勘探, 2008, 43(增刊2): 70-73. ] [本文引用:2] [CJCR: 1.333]
[9]	Duan Yunqing, Pi Jinyun, Liu Bing, et al. Study on near-surface survey by 3-component(3-C)shallow refraction[J]. Oil Geophysical Prospecting, 2008, 43(6): 652-655. [段云卿, 皮金云, 刘兵, 等. 三分量小折射表层调查研究[J]. 石油地球物理勘探, 2008, 43(6): 652-655. ] [本文引用:1] [CJCR: 1.333]
[10]	Zhang Wei, He Zhengqin, Hu Gang, et al. Detection of the shallow velocity structure with surface wave prospection method[J]. Progress in Geophysics, 2013, 28(4): 2199-2206. [张维, 何正勤, 胡刚, 等. 用面波联合勘探技术探测浅部速度结构[J]. 地球物理学进展, 2013, 28(4): 2199-2206. ] [本文引用:1] [CJCR: 2.178]
[11]	Zhang Kai, Li Zhenchun. Tomographic velocity inversion method with dual-complexity[J]. Progress in Geophysics, 2013, 28(6): 3001-3006. [张凯, 李振春. 双复杂条件下层析速度反演方法研究[J]. 地球物理学进展, 2013, 28(6): 3001-3006. ] [本文引用:1] [CJCR: 2.178]
[12]	Bai Chaoying, Stewart Greenhalgh, Zhou Bing. 3D ray tracing using a modified shortest-path method[J]. Geophysics, 2007, 72(4): T27-T36. [本文引用:1] [JCR: 1.723]
[13]	Sang Yunyun, Li Zhenchun, Zhang Kai. Shortest path ray tracing based on parabolic traveltime interpolation[J]. Oil Geophysical Prospecting, 2013, 48(3): 403-409. [桑运云, 李振春, 张凯. 基于抛物旅行时插值的最短路径射线追踪[J]. 石油地球物理勘探, 2013, 48(3): 403-409. ] [本文引用:1] [CJCR: 1.333]
[14]	Zhou H. Multiscale traveltime tomography[J]. Geophysics, 2003, 68(5): 1639-1649. [本文引用:1] [JCR: 1.723]
[15]	Liu Hui, Zhou Huawei, Liu Wenge. Tomographic velocity model building of the near surface with velocity-inversion interfaces: A test using the Yilmaz model[J]. Geophysics, 2010, 75(6): 39-47. [本文引用:1] [JCR: 1.723]
[16]	Tailland ier C, Noble M, Chauris H, et al. First-arrival traveltime tomography based on the adjoint-state method[J]. Geophysics, 2009, 74(6): WCB1-WCB10 [本文引用:1] [JCR: 1.723]
[17]	Woodward M J. Wave-equation tomography[J]. Geophysics, 1992, 57: 15-26. [本文引用:1] [JCR: 1.723]
[18]	Dahlen F A, Hung S H, Nolet G. Fréchet kernels for finite-frequency travel-times-I. Theory[J]. Geophysical Journal International, 2000, 141(1): 157-174. [本文引用:1] [JCR: 2.853]
[19]	Schuster G T, Quintus-Bosz A. Wavepath eikonal traveltime inversion: Theory[J]. Geophysics, 1993, 58(9): 1314-1323. [本文引用:1] [JCR: 1.723]
[20]	Luo Y, Schuster G T. Wave-equation traveltime inversion[J]. Geophysics, 1991, 56(5): 645-653. [本文引用:1] [JCR: 1.723]
[21]	Vasco D W, Peterson J E, Jr Ernest L, et al. Beyond ray tomography: Wavepaths and Fresnel volumes[J]. Geophysics, 1995, 60(6): 1790-1804. [本文引用:1] [JCR: 1.723]
[22]	Ĉervený V, Soares J. Fresnel volume ray tracing[J]. Geophysics, 1992, 57: 902-915. [本文引用:1] [JCR: 1.723]
[23]	He L, Zhang W, Zhang J, et al. 3D wave-ray traveltime tomography for near-surface imaging[C]//83th Annual International Meeting, SEG, Expand ed Abstracts, Houston, American, 2013: 1 749-1753. [本文引用:1]
[24]	Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. [本文引用:3] [JCR: 1.723]
[25]	Wang Huazhong, Wang Xiongwen, Wang Xiwen. Analysis of the basic problems of seismic wave inversion[J]. Lithologic Reservoirs, 2012, 24(6): 1-9. [王华忠, 王雄文, 王喜文. 地震波反演的基本问题分析[J]. 岩性油气藏, 2012, 24(6): 1-9. ] [本文引用:2] [CJCR: 2.2884]
[26]	Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. [本文引用:1] [JCR: 1.723]
[27]	Bian Aifei, Yu Wenhui, Zhou Huawei. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics, 2010, 25(3): 982-993. [卞爱飞, 於文辉, 周华伟. 频率域全波形反演研究进展[J]. 地球物理学进展, 2010, 25(3): 982-993. ] [本文引用:1] [CJCR: 2.178]
[28]	Lailly P. The seismic inverse problem as a sequence of before stack migrations[C]// Conference on Inverse Scattering: Theory and Applications. Philadelphia: SIAM, 1984: 206-220. [本文引用:1]
[29]	Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. [本文引用:5]
[30]	Pratt R G. Frequency-domain elastic modeling by finite differences: A tool for cross hole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. [本文引用:1] [JCR: 1.723]
[31]	Pratt R G. Seismic waveform inversion in the frequency domain, part I: Theory and verification in a physic scale model[J]. Geophysics, 1999, 64(3): 888-901. [本文引用:1] [JCR: 1.723]
[32]	Plessix R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. [本文引用:1] [JCR: 2.853]
[33]	Gauthier O, Virieux J, Tarantola A. Two-dimensional nonlinear inversion of seismic waveform: Mumeical results[J]. Geophysics, 1986, 51(7): 1387-1403. [本文引用:1] [JCR: 1.723]
[34]	Mora P. Nonlinear two-dimensional elastic inversion of multi-offset seismic data[J]. Geophysics, 1987, 52(9): 1211-1228. [本文引用:1] [JCR: 1.723]
[35]	Pratt R, Sams M. Reconciliation of cross hole seismic velocities with well information in a layered sedimentary environment[J]. Geophysics, 1996, 61(2): 549-560. [本文引用:1] [JCR: 1.723]
[36]	Pratt R, Shin C, Hicks G. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal international, 1998, 133(2): 341-362. [本文引用:1] [JCR: 2.853]
[37]	Sirgue L, Barkved O I, Dellinger J, et al. Full waveform inversion: The next leap forward in imaging at Valhall[J]. First Break, 2010, 28(1): 65-70. [本文引用:1]
[38]	Plessix R, Perkins C. Full waveform inversion of a deep water ocean bottom seismometer dataset[J]. First Break, 2010, 28(1): 71-78. [本文引用:1]
[39]	Hu G, Etieen V, Castellanos C, et al. Assessment of 3d acoustic isotropic full waveform inversion of wide-azimuth obc data from valhall[C]//Expand ed Abstracts of 82th Annual International Meeting, SEG, Expand ed Abstracts, Las Vegas, America, 2012: 1-6. [本文引用:1]
[40]	Shin C. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J]. Geophysics, 2012, 77(5): 199-206. [本文引用:1] [JCR: 1.723]
[41]	Plessix R, Baeten G, Villem J. Full waveform inversion and distance separated simultaneous sweeping: A study with a land seismic data set[J]. Geophysical Prospecting, 2012, 60(4): 733-747. [本文引用:1] [JCR: 1.36]
[42]	Hu G, Fang W, Jia C, et al. Full waveform inversion technology and its application[J]. Geophysical Prospecting for Petroleum, 2013, 51(SI): 90-96. [本文引用:1] [CJCR: 1.224]
[43]	Hu Guanghui, Jia Chunmei, Xia Hongrui, et al. Implementation and validation of 3D acoustic full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 417-425. [胡光辉, 贾春梅, 夏洪瑞, 等. 3D声波全波形反演的实现及应用[J]. 石油物探, 2013, 52(4): 417-425. ] [本文引用:2] [CJCR: 1.224]
[44]	Yang Qinyong, Hu Guanghui, Wang Lixin. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 78-84. [杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状与发展趋势[J]. 石油物探, 2014, 53(1): 78-84. ] [本文引用:1] [CJCR: 1.224]
[45]	Sheng J, Leeds A, Buddensiek M, et al. Early arrival waveform tomography on near-surface refraction data[J]. Geophysics, 2006, 71(4): U47-U57. [本文引用:3] [JCR: 1.723]
[46]	Levand er A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1437. [本文引用:1] [JCR: 1.723]
[47]	Berenger J. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114: 185-200. [本文引用:1] [JCR: 2.138]
[48]	Chew W, Liu Q. Perfectly matched layers for elastrodynamics[J]. Journal of Computational Acoustics, 1996, 4: 341-359. [本文引用:1] [JCR: 0.69]
[49]	Zeng Y, He J Q, Liu Q. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media[J]. Geophysics, 2001, 66: 1258-1266. [本文引用:1] [JCR: 1.723]
[50]	Festa G, Nielson S. PML absorbing boundaries[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 891-903. [本文引用:1] [JCR: 1.94]
[51]	Zhou C, Cai W, Luo Y, et al. Acoustic wave-equation traveltime and waveform inversion of crosshole seismic data[J]. Geophysics, 1995, 60(3): 765-773. [本文引用:2] [JCR: 1.723]
[52]	Zhou C, Schuster G T, Hassanzadeh S, et al. Elastic wave-equation traveltime and waveform inversion of crosshole seismic data[J]. Geophysics, 1997, 62(3): 853-868. [本文引用:1] [JCR: 1.723]
[53]	Causse E, Mittet R, Ursin B. Preconditioning for full-waveform inversion in viscoacoustic media[J]. Geophysics, 1999, 64(2): 130-145. [本文引用:1] [JCR: 1.723]
[54]	Nocedal J, Wright S J. Numerical Optimization[M]. New York: Springer-Verlag, 1999. [本文引用:1]
[55]	Nemeth T, Normark E, Qin F. Dynamic smoothing in crosswell traveltime tomography[J]. Geophysics, 1997, 62(1): 168-176. [本文引用:1] [JCR: 1.723]
[56]	Hanafy S M, Yu H. Early arrival waveform inversion of shallow seismic land data[C]//83th Annual International Meeting, SEG, Expand ed Abstracts, Houston, American, 2013: 1 738-1742. [本文引用:1]
[57]	Sirgue L, Pratt R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248. [本文引用:3] [JCR: 1.723]
[58]	Boonyasiriwat C, Valasek P, Routh P, et al. An efficient multiscale method for time-domain waveform tomography[J]. Geophysics, 2009, 74(6): WCC59-WCC68. [本文引用:1] [JCR: 1.723]
[59]	Boonyasiriwat C, Schuster G T, Valasek P, et al. Applications of multiscale waveform inversion to marine data using a flooding technique and dynamic early-arrival windows[J]. Geophysics, 2010, 75(6): R129-R136. [本文引用:1] [JCR: 1.723]
[60]	Boonyasiriwat C, Valasek P, Routh P, et al. Application of multiscale waveform tomography for high-resolution velocity estimation in complex geologic environments: Canadian Foothills synthetic data example[J]. The Leading Edge, 2009, 28(4): 454-456. [本文引用:1]
[61]	Rabine L R, Gold B. Theory and Application of Digital Signal Processing[M]. New Delhi: Prentice-Hall, 1975. [本文引用:1]
[62]	Oldenburg D W, Levy S, Whittall K P. Wavelet estimation and deconvolution[J]. Geophysics, 1981, 46(11): 1528-1542. [本文引用:1] [JCR: 1.723]
[63]	Lazear G D. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. [本文引用:1] [JCR: 1.723]
[64]	Walden A T, White R E. Seismic wavelet estimation: A frequency domain solution to a geophysical noisy input-output problem[J]. IEEE Transactionson Geoscience and Remote Sensing, 1998, 36: 287-297. [本文引用:1]
[65]	Behura J. Virtual real source[C]//77th Annual International Meeting, SEG, Expand ed Abstracts, San Antonio, America, 2007: 2 693-2696. [本文引用:1]
[66]	Maresh J, White R S, Hobbs R W, et al. Seismic attenuation of Atlantic margin basalts: Observations and modeling[J]. Geophysics, 2006, 71(6): B211-B221. [本文引用:1] [JCR: 1.723]
[67]	Wang Y. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71, (3): V51-V60. [本文引用:1] [JCR: 1.723]
[68]	Zou Z, Ramos-Martínez J, Kelly S, et al. Refraction full-waveform inversion in a shallow water environment[C]//76th Conference and Exhibition, EAGE, Extended Abstracts, Amesterdam, Holland , 2014. [本文引用:1]
[69]	McNeely J, Keho T, Tonellot T, et al. 3D acoustic waveform inversion of land data: A case study from Saudi Arabia[C]//82th Annual International Meeting, SEG, Expand ed Abstracts, Las Vegas, America, 2012: 1-5. [本文引用:1]
[70]	Dong Liangguo, Chi Benxin, Tao Jixia, et al. Objective function behavior in acoustic full-waveform inversion[J]. Chinese Journal Geophysics, 2013, 56(10): 3445-3460. [董良国, 迟本鑫, 陶纪霞, 等. 全波形反演目标函数性态[J]. 地球物理学报, 2013, 56(10): 3445-3460. ] [本文引用:1] [CJCR: 0.5277]
[71]	Shen X. Near-surface velocity estimation by weighted early-arrival waveform inversion[C]//80th Annual International Meeting, SEG, Expand ed Abstracts, Denver, America, 2010: 1 975-1979. [本文引用:1]
[72]	Speziali M, Re S, Clementi M, et al. Near-surface characterization in using simultaneous joint inversion of refracted and surface waves—A case study[C]//76th Conference and Exhibition, EAGE, Extended Abstracts, Amesterdam, America, 2014. [本文引用:1]
[73]	Colombo D, Rovetta D, Sand oval C E, et al. 3D seismic-gravity simultaneous joint inversion for near surface velocity estimation[C]//75th Conference and Exhibition, EAGE, Extended Abstracts, 2013. [本文引用:1]
[74]	Gao Y, Chen X, Hu H, et al. Early electromagnetic waves from earthquake rupturing: II. Validation and numerical experiments[J]. Geophysical Journal International, 2013, 192: 1308-1323. [本文引用:1] [JCR: 2.853]
[75]	Liu Xinming, Liu Shucai, Yi Hongchun, et al. The simulation research of electromagnetic wave attenuation coefficient tomography in media of complicated fault structures[J]. Advances in Earth Science, 2013, 28(3): 391-397. [刘鑫明, 刘树才, 易洪春, 等. 复杂断层构造电磁波衰减系数层析成像模拟研究[J]. 地球科学进展, 2013, 28(3): 391-397. [本文引用:1] [CJCR: 1.388]

2013

0.0

1.388

. 2013, 28(1):51-61

Hot topics and trends in the study of high arsenic groundwater

1.State Key Laboratory of Biogeology and Environmental Geology, China University of Geosciences, Beijing100083, China; 2.School of Water Resources and Environment, China University of Geosciences, Beijing100083, China

High-arsenic groundwater widely spreads in the world, which has posed a great threat to human health. Mechanisms of arsenic mobilization in aquifer systems have been considered to be worldwide scientific issues. We outline characteristics of spatial distribution of high-arsenic groundwater and arsenic enrichment mechanisms. Controls of dissolved organic matter and groundwater flow on arsenic mobilization in groundwater are reviewed and discussed. Recent studies reveal synergistic effect of dissolved organic matter and microbial processes on genesis of high arsenic groundwater. Spatial and temporal variations of higharsenic groundwater and anthropogenic activities affecting the high-arsenic groundwater distribution have recently been characterized, and gradually become the hot topics in this field. These aspects are of great significance in enriching our understanding of transportation and transformation in aquifer systems and finding low-arsenic water resources for sustainable water development in arsenic-affected areas.

全球范围内广泛分布的高砷地下水给人们的健康造成了极大的威胁。高砷地下水的形成机理是一项世界性的科学问题。介绍了高砷地下水的分布特点、富集机理，阐明了溶解性有机物、地下水流动特征对高砷地下水形成的影响机制。现今的研究揭示了有机物和微生物协同作用下高砷地下水的形成过程，并且在高砷地下水的空间分布、时间变化特征以及人类活动对高砷地下水形成的影响等方面取得了一些创新性成果。这3方面的研究也逐渐成为近些年高砷地下水研究的热点。这些研究不仅丰富了砷迁移转化的理论成果，而且有助于开辟低砷水源，保障水资源的可持续利用，具有重要的理论和现实意义。

... 1 引言随着世界经济对油气、地下水^[1]、矿产等资源需求量的日益增加,勘探力度逐步加大,这就对高精度建模成像技术提出了更高的要求 ...

2013

0.0

1.333

. 2013, 48(1):151-159

Seismic exploration strategy and inmage processing in mountain areas

山前带地震资料信噪比低和道间时差剧变是引起此类地区成像困难的主要原因。本文从宏观速度估计的角度，分析了山前带勘探中野外数据采集、资料低信噪比和道间时差剧变等因素与后续成像处理的关系，认为速度建模是山前带成像处理的关键问题，山前带地震数据采集要以有利于近地表浅层速度建模和中深层宏观速度估计为目标。为此，本文提出了一套以宏观速度建模为核心的成像处理流程。在该流程中首先利用基于叠前深度偏移(PSDM)的扫描速度分析方法得到初始宏观速度场；再利用非水平地表射线束PSDM技术高效生成深度域成像道集；最后进行角度道集层析速度估计，为射线束PSDM提供更精细速度模型。压噪和消除道间时差是该流程的两个关键环节。本文强调尽可能用同相叠加方法压制噪声，通过选取合适成像基准面以消除或减弱高波数道间时差对叠前成像的影响；中低波数道间时差由后续速度分析及成像消除，将静校正问题置于速度建模过程中加以解决。理论模型和实际资料成像结果验证了本文思路的正确性及方法的有效性。

... 因此,如何提高近地表速度模型精度将是复杂地表成像处理的关键问题^[2],近地表速度模型的精确重建对近地表的矿产普查,工程物探^[3]以及改善近地表复杂区老油田成像精度,提高油气产量具有重要意义 ...

2012

0.0

1.388

. 2012, 27(11):1185-1191

Basic research on the major permafrost projects in the Qinghai-Tibet Plateau

State Key Laboratory of Frozen Soils Engineering, Cold and Arid Environmental and Engineering Research Institute, Chinese Academy of SciencesLanzhou, 730000, China

QinghaiTibet Plateau is representative highaltitude permafrost region on the earth. Along with the operation of Qinghai-Tibet Railway, a new round of economic development in Xizang (Tibet) Autonomous Region has emerged, which need construction of highway, power transmission line and oil/gas pipeline. These proposed projects and already existed projects, including QinghaiTibet Railway, Qinghai-Tibet Highway, Golmud-Lhasa oil product pipeline, and optical cable from Lanzhou to Lhasa, are all located in the QinghaiTibet engineering corridor, which is not wide than 10 km. In this corridor, influences between proposed and existed projects and coupling of multifactors will accelerate the permafrost degradation, and consequently undermine the stability of these projects and ecological environment, especially along with climate change. To meet the national needs, “Basic Research on the Major Permafrost Projects in the Qinghai-Tibet Plateau”, a project of National Basic Research Program of China, was initiated in April, 2012. The aim of this project is to reveal the spacetime revolution of permafrost and permafrostrelated hazards under the scenarios of climate change and intensive engineering activity, construct an evaluation system on stability and service ability of permafrost engineering, and propose a preventative theory and control measures on permafrost engineering hazard, and finally provide scientific guidelines on prearranging plan on permafrost engineering hazard and on construction of major permafrost engineering in the future.

青藏高原是我国乃至世界高海拔多年冻土区的典型代表。伴随着青藏铁路的建成通车，西藏自治区迎来了新一轮经济发展，迫切需要新建高速公路、输变电线路、输油气管道工程等。这些拟建工程与已建的青藏公路、青藏铁路、格拉输油管道、兰西拉光缆等工程均聚集于宽度不足10 km范围内的青藏工程走廊。在这狭长的冻土工程走廊内，已修建或拟建的各种冻土构筑物相互影响，多因素耦合叠加，加速区域内的冻土退化，而冻土融化必将影响到工程的稳定性和生态环境退化。再加上全球气候变化的影响，其变化程度更加剧烈。面对国家需求，国家重点基础研究发展项目“青藏高原重大冻土工程的基础研究”于2012年4月正式启动。该项目旨在揭示气候变化与人类工程活动加剧背景下冻土变化及灾害时空演化规律，建立冻土工程稳定性和服役性能评价体系，提出冻土工程灾害防治理论与控制对策，为冻土构筑物群灾害应急预案和重大冻土工程建设提供科学决策依据。

2014

0.0

. 2014, 29(1):255-260 DOI:10.6038/pg20140136

The research of travel time tomographic velocity modeling method on first break

1. Geophysical Research Institute of Sinopec Shengli Oilfield, Postdoctoral Scientific Research Workstation of Sinopec Shengli Oilfield, Dongying 257002, China; 2. School of Geosciences, China University of Petroleum, Qingdao 266580, China; 3. Huabei Sub-institute of Research Institute of BGP, CNPC, Renqiu 062550, China

The kernel of tomographic inversion is the solution of sensitive kernel function and the establishing set of travel time equations. Based on the ray theory, ray tracing is the main method to calculate the sensitive kernel function and travel time. Therefore the way to trace first break travel path exactly is needed for first break tomography. In this paper the formula of parabolic travel time interpolation is derived based on the previous research. This paper puts forward the dynamic shortest path ray tracing algorithm using parabolic travel time interpolation. The theoretical model and the real data prove the feasibility of the method, which is used to realize the velocity modeling based on the first break tomography.

层析反演的核心是敏感核函数的求取和旅行时反演方程的建立.在射线理论下，射线追踪技术是计算敏感核函数和旅行时的主要方法，因此初至层析的实现需要有一种可以准确追踪初至波路径的射线追踪方法.本文推导了抛物旅行时插值射线追踪公式，提出了基于抛物旅行时插值的最短路径射线追踪方法.理论模型和实际资料处理结果表明，利用该方法实现初至层析速度建模可行.

... 2 近地表速度建模方法在山地、黄土塬^[4]等复杂地质构造区域,浅表层干扰波强烈,吸收衰减严重、高速岩层出露以及近地表横向速度变化剧烈,使地震波的传播路径变得非常复杂,同时野外施工困难,导致采集到的地震资料信噪比低,道间时差变化剧烈^[5],表层结构调查工作越来越受到人们的重视,出现了很多近地表速度反演方法,如微测井、折射波法、面波法以及走时层析方法等,这几种方法在实际生产中应用比较广泛^[6] ...

2009

0.0

0.6955

. 2009, 21(12):72-76

Development status overview of seismic prospecting technology in loess tableland

黄土塬区的地震勘探技术长期以来-直被认为"世界级"难题,其主要原因有三:一是黄土塬区复杂的地貌条件,即沟、梁、塬、峁、坡、川并存;二是复杂的地表条件,即沟壑纵横施工困难;三是复杂的表浅层条件,即地震波难以激发且能量衰减严重等.在具体分析我国黄土塬区资源分布状况与勘探实践的基础上,对黄土塬区地震勘探数据采集与资料处理的一些技术难点进行了阐述.指出今后在黄土塬区开展地震勘探工作,应从粘弹介质、连续介质的角度,进行地震波激发与传播规律的研究,从地震正演模型和室内模拟的角度,进行黄土塬区的资料采集和处理方法研究,同时要注重引进新技术,加强储层物性横向变化的预测研究.

2009

0.0

0.55

2008

0.0

... 1 微测井微测井是在一口或多口穿过低、降速带的井中,采用井中激发、地面接收,地面激发、井中接收或井中激发、井中接收等方式,利用多次激发而得到的透射波时距曲线的拐点和折射段的斜率来划分低速层、降速层速度和厚度^[7] ...

2008

0.0

1.333

... 利用微测井法调查的表层结构一般比较准确,特别是对于低降速层较厚,速度变化较大的表层结构,其计算精度要优于其他方法,该方法基本不受地表条件的限制,适用范围较广^[8],但这种方法成本高、效率低,一般仅用于表层结构调查的控制点测量 ...

... 因此该方法适用于地表平缓、表层结构简单且低降速层变化较小的区域^[8] ...

2008

0.0

1.333

. 2008, 43(6):652-655

Study on near-surface survey by 3-component(3-C)shallow refraction

为了获取准确的静校正量，给多波多分量勘探提供准确的近地表纵、横波速度和厚度模型，采用炸药震源进行了三条测线的三分量小折射近地表调查，对三分量小折射表层调查技术进行了初步研究，详细地阐述了利用偏振分析方法分离纵横波的原理，并得出以下认识：纵波初至波的矢端曲线的椭圆率较小，线性偏振特性很强；近炮检距的横波初至难以识别，中远炮检距横波初至波的偏振方向比较稳定，能够代表炸药震源激发的横波的偏振方向，其矢端曲线的椭圆率较大。通过对实际资料的联合解释，给出本工区的纵横波低速层和高速层速度比的范围和纵横波静校正量，并总结了一套三分量小折射资料处理解释流程。

... 段云卿等^[9]进行了三分量的小折射的表层研究 ...

2013

0.0

2.178

. 2013, 28(4):2199-2206 DOI:10.6038/pg20130467

Detection of the shallow velocity structure with surface wave prospection method

1. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China; 2. Geophysical Prospecting Company, Chuanqing Drill Engineering Company, Chengdu 610213, China; 3. Jintang People's Procuratorate, Chengdu 610213, China

Rayleigh wave exploration technology has been rapid developed in the resent years and widely used to detect the shallow S-wave velocity structure because of its economy and simple operation. The artificial source Rayleigh wave exploration technology method provides a high precision for shallow structure, but the detection depth is low; on the contrary, the nature source Rayleigh wave exploration technology method would gives a deeper investigation depth, however, the precision for the shallow structure is not so good as the artificial source. We carry out joint exploration engineering cases at Xiadian and Yuxi,in which the different and same arrangements are adopted respectively to collect the data for artificial and nature source. The dispersion curves are separately extracted and then combined to be used in the inversion. The results indicate that in the joint surface wave exploration cases, spatially adopting the same arrangement, the detection precision is ensured, and the detection depth is evidently deeper for the joint exploration method than the method using either active or passive source without increasing the work effort. It shows the joint exploration method will find its potential application in the field of engineering survey domain.

瑞雷面波勘探技术以其快速经济、受场地条件限制小等优点广泛应用于浅部横波速度结构探测.人工源面波勘探方法对浅部地层的探测精度高,但探测深度较浅;天然源面波勘探方法探测深度较深,但对浅部速度结构的探测精度不高.本文在夏垫和玉溪两地分别开展了人工源和天然源面波联合探测试验,尝试采用不同排列和相同排列两种方法,采集人工源和天然源面波信息,联合处理数据并提取频散曲线,反演得到浅部地层的横波速度结构.探测结果表明:人工源和天然源面波联合勘探,尤其是采用相同排列的方法,可以在几乎不增加常规面波勘探工作量的条件下,既能保证浅部地层的探测精度,又明显拓展探测深度,大大提升了面波勘探能力,有望在工程勘察领域中推广应用.

... 张维等^[10]在玉溪和夏垫两地分别开展了天然源和人工源面波联合勘探试验,利用采集到的人工源和天然源面波信息进行数据处理并提取频散曲线,反演浅部地层的横波速度结构,大大提升了面波勘探能力,但在数据采集和处理技术上还存在诸多问题 ...

2013

0.0

2.178

. 2013, 28(6):3001-3006 DOI:10.6038/pg20130622

Tomographic velocity inversion method with dual-complexity

School of Geosciences, China University of Petroleum, Qingdao 266580, China

The exploration for carbonate rock area has the characters of complex surface, steep dip structures, deep target layer and complex reservoir, which make it difficult to process data using conventional methods suited for horizontal layered media and clastic rock media. Pre-stack depth migration method is an effective method to improve imaging quality of carbonate rock data and raise the precision of deep complex structure and lithology imaging. While, high quality migration methods depend on high precision velocity inversion methods. For complex carbonate rock area, the methods of statics plus pre-stack depth migration velocity analysis have limitation in precision. This paper proposes a method of tomographic velocity inversion with dual-complexity, which is the improvement of conventional travel-time tomographic method. This method could update velocity to carbonate rock target layer from complex surface and need not do statics in pre-stack data. Through this method, we can improve the precision and efficiency of velocity inversion. This paper introduces the method to acquire angle-domain common imaging gathers (ADCIGs) on complex surface Gaussian beam migration method on which to perform the tomographic velocity inversion. The tests to model data and field data prove the method to be correct and effective.

地表复杂、地下陡倾构造、极深层目标反射体、复杂储层是碳酸盐岩地震勘探的难点问题.这些特点使得基于水平层状介质假设、适合于碎屑岩的常规处理方法精度有限.叠前深度偏移成像是改善海相碳酸岩地区地震资料质量和提高深层复杂构造与岩性成像精度的最有效的方法.为了能够得到高质量的成像结果，需要有与之相对应的速度反演方法.对于双复杂碳酸盐岩地区，基于静校正的常速替代方法后再进行叠前偏移速度分析精度有限.本文提出的基于双复杂条件的层析速度反演方法是常规走时层析方法的改进，不需要对数据进行静校正处理，从复杂地表直接对碳酸盐岩目标层的速度场更新，从而提高层析速度反演的精度与效率.本文首先介绍了基于高斯束偏移的角度域共成像点道集的提取方法，以此为基础介绍了双复杂条件层析速度反演方法.通过模型和实际资料的试算验证了本文方法的正确性与有效性.

... 4 层析反演方法层析成像最先用于医学,20世纪80年代地震层析成像进入地球物理领域,由于走时层析成像效率高,稳健,实际应用费用低廉,一直是研究热点之一,走时层析通过最小化观测旅行时与计算旅行时之间的差值来计算速度扰动,更新速度场,层析线性方程可以表达为^[11]： ...

2007

1.723

0.0

... 射线追踪是走时层析的核心技术^[12],桑运云^[13]推导了抛物旅行时插值射线追踪公式,提出了基于抛物旅行时插值的最短路径射线追踪方法,克服了最短路径方法中射线#cod#x0201c ...

2013

0.0

1.333

. 2013, 48(3):403-409

Shortest path ray tracing based on parabolic traveltime interpolation

以最短路径射线追踪为基础，受动态网络最短路径射线追踪的启发，本文推导了抛物旅行时插值射线追踪公式，提出了基于抛物旅行时插值的最短路径射线追踪方法。其关键在于对某一计算节点不但利用Dijkstra算法计算旅行时，而且利用已知旅行时的节点形成的插值段进行抛物旅行时插值（PTI），并将两部分得到的最小旅行时作为该计算节点的最终时间，射线路径追踪利用抛物旅行时插值从接收点到炮点反向追踪。模型试算证明了该方法的正确性、有效性和适用性。

2003

1.723

0.0

... Zhou^[14]引入多尺度层析来处理不均匀的射线覆盖,减少层析中的多解性问题,并对南加利福尼亚地壳结构进行了三维测试,验证了利用多尺度层析比传统的单尺度层析能够得到分辨率更高的速度模型 ...

2010

1.723

0.0

... 随后,Liu等^[15]展示了在实际资料中常见的上覆地层速度高于下覆地层速度的Yilmaz速度模型对初至走时层析射线路径、静校正的严重影响,将多尺度可变层层析(Multiscale Deformable-Layer Tomography,DLT)应用到该模型中显著的提高了静校正结果和深层成像精度 ...

2009

1.723

0.0

... Taillandier^[16]采用伴随状态法避免Fr#cod#x000e9 ...

1992

1.723

0.0

... 为了克服走时层析成像的高频局限,近年来,地震勘探工作者做出了很多努力,产生了波路径 ^[17~21]和菲涅耳体层析方法^[22~23] ...

2000

2.853

0.0

1993

1.723

0.0

1991

1.723

0.0

... 反演策略基于Tarantola提出的伴随方法,在最小化目标范数时利用非线性预处理的共轭梯度法^[20],通过正传波场和反传波场残差零延迟互相关来计算目标函数对于速度的梯度^[24,51,52] ...

1995

1.723

0.0

... 为了克服走时层析成像的高频局限,近年来,地震勘探工作者做出了很多努力,产生了波路径 ^[17~21]和菲涅耳体层析方法^[22~23] ...

1992

1.723

0.0

... 为了克服走时层析成像的高频局限,近年来,地震勘探工作者做出了很多努力,产生了波路径 ^[17~21]和菲涅耳体层析方法^[22~23] ...

2013

0.0

... 为了克服走时层析成像的高频局限,近年来,地震勘探工作者做出了很多努力,产生了波路径 ^[17~21]和菲涅耳体层析方法^[22~23] ...

1984

1.723

0.0

... 3 全波形反演全波形反演是当今的研究热点,它基于Bayes理论框架之下,利用叠前地震波场的运动学和动力学信息重建地下物理模型参数,在理论上被认为是建模精度最高的手段,对复杂构造较小储层等具有精细刻画的潜力^[24,25] ...

... 从20世纪80年代Lailly^[28]和Tarantola^[24]分别提出时间域的全波形反演,由于时间域同时反演所有频率成分,使得问题的非线性问题增大,Bunks^[29]提出了时间域的多尺度反演,通过对资料处理分解为不同的空间尺度,从而增加了问题的稳定性,降低了非线性程度 ...

2012

0.0

2.2884

. 2012, 24(6):1-9

Analysis of the basic problems of seismic wave inversion

1. School of Ocean and Earth Science， Tongji University， Shanghai 200092， China； 2. PetroChina Research Institute of Petroleum Exploration & Development-Northwest， Lanzhou 730020， China

FWI（FullWaveform Inversion） which is based on the framework ofBayes theory is the leading technology of seismic exploration. The basic idea of FWI is widely used for de-noising, deconvolution, seismic data regularization, 1D impedance inversion, AVA elastic parameter inversion, pre-stack migration imaging, velocity analyzing and tomography. Due to the nonlinearity between the observed data and inverse model parameters, there are still a lot of difficulties when FWI is used for field data processing. The essence of FWI was presented under the frame of statistic theory firstly. It was pointed out that Bayes estimation can be implemented with least squares by assuming that the noise satisfies Gaussian distribution. Then the mathematics physics meaning of the mapping from data space to model space is explained. And the nonlinearity of this mapping is decided by the nonlinear relationship between data space and model space, or decided by the complexity of the model parameter and forward operator. At last, the strategy which can push the practical use of FWI was presented after the comparison of the characteristics between land data and marine data. It was believed that:①the velocity inversion should be based on CWI（characteristic waveform inversion）, but not FWI;②the proportion of phase error in error function should be increased legitimately; ③the prior information about data space and model space should be considered more adequately. Only by these ways, FWI can be pushed to its practical use.

Bayes 理论框架下的地震波全波形反演是油气勘探中的导引性技术，其基本思想在去噪音、反褶积、地震数据规则化、一维波阻抗反演、AVA（叠前）弹性参数反演、叠前偏移成像、速度分析及层析成像中占据核心位置。但由于观测数据与反演模型参数之间的高度非线性性，导致在实际地震数据处理中地震波全波形反演（FWI）的难度增大。据此，首先从概率论的观点说明了地震波反演的本质，指出在假设观测噪音为高斯白噪的情况下，Bayes 估计可以在最小二乘意义下实现；接着分析了数据空间向参数空间映射的数学物理含义，指出映射的非线性性强弱取决于数据和模型之间的非线性关系，更准确地说取决于介质模型的复杂性和描述地震波物理传播过程的正算子的复杂性；最后在分析陆上和海上地震数据特点的基础上，指出了地震波反演走向实用化的策略。通过以上分析，提出：①速度场的反演是利用特征波场的反演（CWI），而不是全波形的反演；②合理地增加波场的相位信息在泛函中所占的比例；③尽量充分考虑初始模型的先验信息。只有满足以上3 个条件，才能使地震波全波形反演逐步走向实用化。

... 另一方面,王华忠等^[25]分析指出需要合理的增加相位信息在泛函中的比例,综合应用波场中旅行时、相位和振幅的信息 ...

2009

1.723

0.0

... 全波形反演是一个观测数据与计算数据的拟合过程^[26],在数学上是一个高度病态的非线性问题,涉及模型参数化、误差泛函的建立、数据预处理、波场的数值模拟,子波估计等研究内容^[27] ...

2010

0.0

2.178

. 2010, 25(3):982-993 DOI:10.3969/j.issn.1004-2903.2010.03.037

Progress in the frequency-domain full waveform inversion method

1. Center for Geophysical prospecting, China University of Geosciences (Wuhan), Wuhan 430074, China; 2. Tomographic Earth System Imaging Center, China University of Geosciences (Wuhan), Wuhan 430074, China

The full waveform inversion (FWI) method utilizes the kinematic and dynamic information of prestack seismic data to rebuild underground velocity structure. It has the potential of revealing detailed structure and lithology characteristics under complex geological background. FWI can be carried out in the either frequency or time domain. Frequency-domain FWI has the advantages of high computation efficiency and data selection flexibility over its time-domain counterpart. Recent advances in frequency-domain FWI including waveform modeling methods, frequency selection strategies, object function configuration styles, source wavelet processing methods, and gradient precondition methods make it attractive for realistic problems. The multiple local minimal nature of the object function is one of the major obstacles to good reflection waveform inversion results. The frequency-domain damped wavefield inversion method fills the gap between the Laplace-domain and frequency-domain FWI methods. The combination of the three methods can mitigate the strong nonlinearity of the waveform inversion problem.

全波形反演方法利用叠前地震波场的运动学和动力学信息重建地下速度结构,具有揭示复杂地质背景下构造与岩性细节信息的潜力.根据研究需要,全波形反演既可在时间域也可在频率域实现.频率域相对于时间域反演具有计算高效、数据选择灵活等优势.近十几年来频率域全波形反演理论在波场模拟方法、反演频率选择策略、目标函数设置方式、震源子波处理方式、梯度预处理方法等方面取得了进展.目标函数存在大量局部极值的特性是影响反射地震全波形反演效果的重要内在因素之一.如果将Laplace域波形反演、频率域阻尼波场反演、频率域波形反演三种方法有机结合,可以降低反演的非线性程度.

1984

0.0

1995

0.0

... Bunks等^[29]提出时间域多尺度波形层析,利用Hamming-window 滤波器对地震子波和地震数据进行低通滤波,使反演从低频到高频数据依次进行 ...

... 而Bunks等^[29]利用Hamming-window function进行低通滤波对于时间域MWT不是最有效的滤波器 ...

... 通过利用几个频带数据和变化网格大小,多尺度方法^[29]成功的反演了复杂的Marmousi 模型 ...

... Bunks^[29]利用Hamming-windowfunction^[61]对震源子波和数据进行低通滤波 ...

1990

1.723

0.0

... 90年代,Pratt^[30,31]提出了频率域全波形反演,从低频逐步走向高频的策略极大程度的降低了非线性 ...

1999

1.723

0.0

... 90年代,Pratt^[30,31]提出了频率域全波形反演,从低频逐步走向高频的策略极大程度的降低了非线性 ...

2006

2.853

0.0

... 在梯度求取中采用伴随状态法^[32]通过震源正传波场和残差回传波场相关求取梯度,避开了对Fr#cod#x000e9 ...

1986

1.723

0.0

... 20世纪80年代,Gauthier^[33]等和Mora^[34]实现了二维地震资料全波形反演 ...

1987

1.723

0.0

... 20世纪80年代,Gauthier^[33]等和Mora^[34]实现了二维地震资料全波形反演 ...

1996

1.723

0.0

... 随着计算机水平的提高,三维全波形反演在90年代中后期陆续出现^[35,36],2010年,Sirgue等^[37]率先对挪威北海油田OBC数据实现了全波形反演,对浅层气云进行了准确描述,并对周边充气的断裂构造进行了精细的刻画,发展了直接对高精度速度体进行地震资料解释的新思路 ...

1998

2.853

0.0

2010

0.0

2010

0.0

... 随后,全波形反演海上三维实际资料应用陆续出现^[38,39] ...

2012

0.0

... 随后,全波形反演海上三维实际资料应用陆续出现^[38,39] ...

2012

1.723

0.0

... 在缺少低频的情况下,Shin^[40]采用拉普拉斯域联合频率域全波形反演,首先利用拉普拉斯域全波形反演对频率不敏感的特性来恢复长波长分量,继而以此为初始模型利用频率域全波形反演恢复短波长分量实现高精度建模 ...

2012

1.36

0.0

... 2012年,壳牌公司和东方地球物理公司合作实现了二维陆上资料的全波形反演^[41] ...

2013

0.0

1.224

... 针对国内陆上探区特点,Hu^[42]开展了面向目标层的全波形反演研究,结果展示了全波形反演对浅中层建模的积极作用,成像剖面有很大改善,构造与测井信息更加吻合 ...

2013

0.0

1.224

... 胡光辉^[43]通过模型验证分析了全波形反演陆上实际资料应用的困难 ...

... 单尺度波形反演(Single-scale Waveform Tomography,SWT)^[43]和多尺度波形反演(Multiscale Waveform Tomography,MWT)应用到这个数据集 ...

2014

0.0

1.224

... 杨勤勇^[44]指出陆上全波形反演的应用瓶颈在于：①路上地震资料常规三维勘探中采用滚动采集以及观测系统设计多基于反射波勘探,偏移距较小难以满足全波形反演所要求的全方位角、大偏移距观测系统 ...

2006

1.723

0.0

... Sheng^[45]联合初至走时层析与波形反演利用近地表折射数据进行最早波至波形层析(Early arrival waveform tomography),利用初至波反演近地表低波数背景速度场、在L2范数约束的最早波至波形反演反演高波数扰动速度场 ...

... Sheng等^[45]提出的最早至波形层析的新方法(Early-arrival Waveform Tomography,EWT),通过对地震数据加窗仅仅反演最早至波场 ...

... 2 对于MWT的有效的低通滤波传统的时间域波形层析^[45]只利用一个频带数据和一种有限差分网格容易导致局部极小问题 ...

1988

1.723

0.0

... 1 基本原理：以二维声波方程为例,在时间域采用空间四阶时间二阶交错网格有限差分方法正演^[46],模型顶边界应用自由表面边界,其他边界利用完全匹配层(Perfectly Matched Layer,PML)边界^[4750] ...

1994

2.138

0.0

1996

0.69

0.0

2001

1.723

0.0

2003

1.94

0.0

1995

1.723

0.0

... 在反演之前,为了进行3D几何扩散校正,通过在频率域滤波将数据从3D变化到2D^[51],数据中初至前的噪声被切除,通过谱比法^[66]估计衰减因子Q,并利用反Q滤波器^[67]对数据进行补偿,沿着海底反射叠加来估计子波 ...

1997

1.723

0.0

1999

1.723

0.0

... k=1,2,…,kmax表示迭代次数, g=g(r)是速度模型的所有成像点, P是常规的几何扩散预处理因子^[53] ...

1999

0.0

. 1999, :-

Numerical Optimization

A simple numerical example is proposed in this paper to show that the application of the smoothing technique can posssibly result in a sub stantial discrepancy markedly different from opti mal mesh in a convex region. This demonstrates the necessity of aPplying mathematical programming to the mesh optimization.

构造了一个简单算例来显示在凸域中应用修匀技术也可能产生一个与最优网格相差很大的结果，进而说明在网格几何优化中应用数学规划法的必要性．

... 式中: λk是步长,由二次线性搜索方法确定^[54] ...

1997

1.723

0.0

... 每一次迭代,利用一次正演和一次反投影来计算梯度方向,初始模型 c0(r)是旅行时层析结果^[55] ...

2013

0.0

... Hanafy等^[56]利用最早波至波形反演方法,基于可控震源激发,最大偏移距232 m的观测系统在Wadi Qudaid开展了探测地下水储藏潜力的研究,合成数据和实际资料结果表明最早波至波形反演比初至走时层析能更加精细地刻画地下速度结构,并指出用最早波至波形反演方法可以提高18%的储藏潜力,展现了巨大的经济效益 ...

2004

1.723

0.0

... 在频率域,Sirgue等^[57]提出了一种最优频带选择策略,极大地减少了波形反演的计算量,把这种方法应用到时间域,2009年,Chaiwoot Boonyasiriwats结合Bunks等提出的多尺度层析以及Sirgue等在频率域提出的最优频带选择策略将Sheng等的方法推进一步,不再是仅仅利用折射数据,而利用全波场信息,通过滤波并选择最优频带在时间域运用分频带和变化网格相结合的方法来克服波形反演中的严重局部极小值问题,分步骤、分尺度的联合初至走时层析和全波形反演进行近地表速度建模,提高了收敛速度和计算效率,精确地恢复了速度模型的低波数成分和高波数成分^[58~60] ...

... 3 最优频带选择策略Sirgue 等^[57]提出的在频率域波形反演中选择最优频带范围策略被延伸到时间域来减少恢复的速度结构中的波数冗余 ...

... Sirgue等^[57]提出的选择频带公式是: ...

2009

1.723

0.0

2010

1.723

0.0

2009

0.0

1975

0.0

... Bunks^[29]利用Hamming-windowfunction^[61]对震源子波和数据进行低通滤波 ...

1981

1.723

0.0

... 震源子波在反演之前已经被估计得到^[62~65] ...

1993

1.723

0.0

1998

0.0

2007

0.0

... 震源子波在反演之前已经被估计得到^[62~65] ...

2006

1.723

0.0

2006

1.723

0.0

2014

0.0

... 一些专业公司在近地表建模方面做了很多工作,PGS公司^[68]在北海(North Sea)利用折射波和回折波的特征波全波形反演对浅水地质环境进行速度建模,反演得到高分辨率速度模型,小尺度异常体得到了精确刻画,偏移成像和共成像点道集均展现出了其优于反射层析结果 ...

2012

0.0

... 沙特阿拉伯石油公司和GeoTomo ^[69]公司将最早至波形反演应用到Saudi Arabia的三维陆上地震数据,结果显示比走时层析结果提高了喀斯特地形特征的纵横向分辨率,并反演得到走时层析所未反演出的高速层 ...

2013

0.0

0.5277

. 2013, 56(10):3445-3460

Objective function behavior in acoustic full-waveform inversion

State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China

The main difficulty in seismic full-waveform inversion is the strong nonlinearity, which is caused by the complexity of seismic wave propagation. The analysis of the behavior of the objective function variation with the parameter perturbation scale can help us to choose the reasonable inversion method and strategy. According to Jannane's method to analyze the objective function behavior, the relationship between the objective function calculated by different seismic data subset and the parameter perturbation scale is studied, especially the nonlinearity. The analysis results will provide some theoretical guidance for FWI to implement the multi-step and multi-scale inversion strategy.

地震波传播的复杂性所引起的地震反演中强烈的非线性问题是目前全波形反演在技术上遇到的最大难题,了解全波形反演中不同的目标函数随不同物性参数的不同摄动尺度的变化性态,对选择合理的反演方法和反演策略具有重要意义.本文参照Jannane等对波形反演目标函数性态的分析方法,通过变密度声波方程,分析了多种地震数据子集的不同目标函数随物性参数的摄动尺度的变化关系,重点分析了它们的非线性程度,为进行分步骤、分尺度全波形反演方法和反演策略的选择提供了理论指导.

... 通过修改目标函数来降低非线性问题,董良国等^[70]分析了不同目标函数随不同物性参数的不同扰动尺度的变化性态,Shen^[71]通过加入更多的相位信息修改目标函数,降低波形,振幅的敏感性,减少非线性程度,对传统的L2范数波形反演实用化具有更进一步的推动作用 ...

2010

0.0

2014

0.0

... 此外,该方法结合面波勘探^[72]以及其他非地震方法如高精度重力法^[73],浅层电磁法^[74~75]及电阻率法进行近地表高精度速度建模具有广泛的应用前景 ...

2013

0.0

2013

2.853

0.0

2013

0.0

1.388

. 2013, 28(3):391-397

The simulation research of electromagnetic wave attenuation coefficient tomography in media of complicated fault structures

1. School of Resource and Earth Science, China University of Mining & Technology, Xuzhou 221116, China;2. State Key Laboratory for Geomechanics & Deep Underground Engineering, CUMT, Xuzhou 221008, China)

Traditional mine electromagnetic wave perspective tomography techniques only consider the propagation distance while ignoring the directionality of transmission which causes the resolution of tomographic imaging to be lower in the detection of complex structure. According to the propagation law of electromagnetic waves in coal medium, a new amplitude attenuation constant involving incidence angle is deduced in this paper. Base on the algebraic reconstruction algorithm, tomography mathematical model is built by introducing the new amplitude attenuation constant, and the software is compiled. The new method is used to do simulation for parallel faults models and cross faults models respectively. By comparison with the traditional method, the results show that the improved amplitude attenuation constant has better effect and it can accurately and clearly indicate position, trend and extension length of complicated fault structures. In addition, the results also show that absolute attenuation tomography method is much more superior to the relative attenuation tomography method in case of attenuation value of media background not being easy to be determined. The resolution of parallel faults is higher than that of cross faults. Finally, a successful example of locating a hidden parallel faults in a coal working face indicates that the effect is enhanced a lot by adopting the improved attenuation constant tomography technique.

传统矿井电磁波透视层析成像技术只考虑电磁波的传播距离而忽视传播的方向性，造成探测复杂构造时的层析成像分辨率较低。依据电磁波在煤岩介质中的传播规律推导出了与入射角有关的新振幅衰减常数。引用新振幅衰减常数并基于代数重建算法建立了层析成像数学模型，编制了程序软件。利用新振幅衰减常数层析成像算法分别对平行和交叉断层进行数值模拟。通过与传统衰减常数层析成像的效果进行对比，结果表明：改进后的新振幅衰减常数层析成像效果更好，对断层的位置、走向、延展长度等情况反映清晰准确；在介质背景衰减场不易确定的情况下，绝对衰减层析成像方式优于相对衰减层析成像方式；平行关系的断层构造分辨率要高于交叉关系的断层构造。通过在某采煤工作面的电磁波层析成像中成功圈定了一组隐伏的平行断层构造实例，说明采用新衰减常数的层析成像技术效果提高明显。