地下水流与溶质迁移模型的研究涉及3方面问题, 一是地下水流模型；二是溶解在地下水中溶质的迁移模型；三是非混溶状态下的溶质迁移模型, 即多相流模型。含水层中地下水流问题是描述地下水溶质迁移问题的基础, 对于非均质介质中的溶质迁移, 很多情况下出现“反常”扩散, 无法应用传统对流-弥散理论对其进行描述, 近年来, 许多学者开始质疑传统对流—弥散模型所基于的理想假设给现实含水层地下水溶质迁移问题的描述和模拟带来了不可避免的误差和缺陷, 非菲克迁移模型（Non-Fick transport model）在描述非均质含水层中地下水溶质迁移得到了快速发展, 理论模型主要有连续时间随机游动（Continuous Time Random Walk, CTRW）理论^{[ 9]}和分数阶对流—弥散方程（fADE）理论^{[ 10]}。这些模型在描述溶质在非均质介质中的迁移比传统对流-弥散理论具有一定的优势, 成为近年来非均质溶质迁移理论研究的热点。许多学者为验证2种理论在描述非均质介质中溶质迁移方面开展了大量的示踪试验^{[ 11, 12]}和数值模拟^{[ 13, 14]}研究。Neuman 等^{[ 15]}系统分析了非均质多孔介质中非菲克迁移的4种理论模型（即经典对流—弥散模型（ADE）、随机对流—弥散模型（stnADE）、连续时间随机游动模型（CTRW）和分数阶对流—弥散模型（fADE）的研究进展, 指出了各种模型的优缺点, 认为分数阶对流—弥散模型最大的缺陷是分数阶量纲的物理意义尚未清楚, 而随机对流—弥散模型是4种模型中最具前景的模型。

自Li等^{[ 16]}于1975年在数学中第一次引入了"混沌"概念以来, 混沌对流问题也成为地下水渗流与污染物迁移模型研究的热点^{[ 17, 18]}。在地下水污染物迁移研究方面, 从污染物迁移扩散的角度考虑, 混合作用对于地下水污染问题来说是具有负面影响的, 因为混合得越好, 含水层中滞留的污染物越多。而从修复的角度而言, 情况却完全相反, 因为在进行场地地下水污染修复时, 如何使得注入的修复溶剂和污染地下水充分混合却成为了修复效率高低的关键。基于这一点, 近年来, 一些学者^{[ 19, 20]}通过研究混沌对流使得污染物充分混合, 应用数值模拟的方法设计一系列抽水井和注水井, 从而为含水层污染修复提供科学依据。尽管这一设想一提出, 就受到了有关学者的质疑^{[ 21]}和争论^{[ 22]}。但是, 这说明人们开始尝试将非线性科学理论引入到地下水渗流与污染物迁移研究之中。

从模型的角度来看, 矩分析方法是定量化研究地下水溶质迁移必不可少的工具。从研究地下水溶质运移的角度出发, 矩又分为空间矩和时间矩, 两者各有优缺点。空间矩分析是Aris^{[ 23]}最先用来描述溶质在流体管道中流动的弥散问题。从空间矩的前三阶矩的定义来看, 零阶矩代表注入含水层中污染物的质量, 也就是通过已知数个空间分布点的浓度值, 计算注入含水层中的溶质的质量。Freyberg^{[ 24]}用空间矩方法分析Borden场地基于对流-弥散非反应示踪剂的数据。这个分析集中关注浓度分布的零阶、一阶和二阶空间矩。对这些矩求积分可获得溶解羽状物的质量、溶质平均速度以及弥散通量。Roberts等^{[ 25]}描述了Borden场地地下水中有机溶质的吸附、阻滞和转化过程。Sudicky^{[ 26]}讨论了含水层水力传导系数的空间变异性及其与溶质质量平均运动的关系。另一个大尺度的野外场地自然梯度示踪试验是在Massachusetts Cape Cod一个砂砾含水层中进行, 主要是研究反应和非反应示踪剂迁移和扩散^{[ 27, 28]}问题。Cape Cod场地研究的一个主要目的是检验Dagan^{[ 5]}和 Gelhar等^{[ 7]}所提出的理论模型。在这项研究中, 将一个含有反应和非反应示踪剂以脉冲的方式注入到含水层中, 依据含水层水力传导系数的空间变异性统计特征来估算弥散度的空间分布, 并将预测结果与空间矩分析所计算的弥散度进行对比。Garabedian等^{[ 27]}给出了Cape Cod场地非反应示踪剂溶质（溴化物）迁移的空间矩分析结果, Goltz等^{[ 29]}用Aris提出的改进对流-弥散溶质迁移方程的三维形式研究空间矩, 其中溶质弥散到不动水区域。Govindaraju等^{[ 30]}在其专著中系统介绍了地下水污染物迁移偏微分控制方程的理论矩分析, 主要关注一维问题的矩分析和理论推导。总之, 矩分析方法为描述非均质含水层中地下水溶质迁移特征提供了重要的理论依据。

尺度问题是很多学科共同面临的问题, 从水文地质结构看, 地下含水层具有多尺度特征, 根据不同研究目的选用不同的尺度。目前国际上比较流行有2种划分方法, 第一种是Dagan^{[ 31]}提出的将含水层分为3种基本尺度, 即：实验室尺度、局部尺度和区域尺度。第二种是由Koltermann等^{[ 32]}根据孔隙介质的沉积结构、沉积环境和地质特征, 将含水层尺度分为多重孔隙尺度、流动特征尺度、地层层状特征尺度、流动通道尺度、沉积环境尺度和流域尺度等。每种尺度的主要特征, 如表1所示。

尺度转换问题（升尺度）成为近年来地下水渗流和溶质迁移研究的难点和热点问题之一。升尺度方法通常包括统计平均法, 体积平均法, 均匀化理论和重正化技术, 而升尺度通常包括参数升尺度和过程升尺度两种^{[ 33]}。由于升尺度对于解决野外现场污染物迁移行为十分重要, 近20年来受到了许多环境和水文地质学者的广泛关注。目前参数升尺度研究主要有非均质含水层的渗透系数升尺度问题^{[ 34, 35]}, 裂隙网络模拟的升尺度问题^{[ 36]}, 阻滞因子的升尺度^{[ 37]}, 升尺度对溶质迁移的影响^{[ 38, 39]}以及高度非均质三维含水层中的渗流^{[ 40]}和溶质运移^{[ 41]}等问题的升尺度研究。最近, Frippiat等^{[ 42]}对比分析了非均质含水层中溶质迁移问题的两种升尺度方法：即非均质参数（弥散度）升尺度和迁移方程升尺度（本质上与上述参数升尺度和过程升尺度相同）, 每种方法均包含3种模型。Dagan等^{[ 43]}系统介绍了不同非均质介质中渗流计算的升尺度模型和方法, 包括层状含水层、三维各向异性含水层、平稳和非平稳随机介质的含水层以及井附近渗流的升尺度问题。

表1

Table 1

表1(Table 1)

表1 沉积非均质性尺度分类表[ 32] Table 1 Classification of scales of sedimentary heterogeneity[ 32] 尺度 相似长度的尺度因素/m 地质特征 影响非均质性的因素 观测/测量技术 水力传导系数观测值的体积平均 多重孔隙尺度 10-6 颗粒的大小和形状、分选、填塞过程、组分胶结以及粘土裂隙 孔隙结构来源、成岩、沉积过程以及沉积物运移机制 观测岩样横断面、岩屑团粒结构, 采集透镜体, 涉及若干个孔隙结构（用微渗透仪观测） 流动特征尺度 10-3 基本沉积结构；细小水流, 交叉贯穿地层, 层面结构, 裂隙分布错位, 软沉积层的变形等 不均匀成岩过程, 沉积物传输机制, 生物活动作用 岩心取样, 手工取样, 观察露头 岩心取样（用渗透仪测量） 地层特征尺度 101 具有丰富的沉积结构, 沉降分选过程 层边界, 细微通道, 带状沙丘 观测露头, 岩性和分析地球物理测井 井的影响范围 流动通道尺度 101~102 流动通道的几何结构, 层理类型和延展性, 岩性和矿物含量 页岩层出现频率, 砂层和页岩体的几何结构, 沉积填充组合 观测露头, 井剖面X线断层影像, 岩性和地球物理测井 局部试验（短期抽水或示踪试验） 沉积环境尺度 102~104 多重复合相位关系, 地层形态特征 裂隙, 内部盆地对流动和沉积机制的控制 地图, 地层剖面岩性和地球物理测井, 地震剖面测井 区域试验（长期抽水或示踪试验） 流域尺度 大于105~ 流域几何特征, 地层的几何特征, 结构特征, 岩相不连续性, 地层的区域走向 断层（封闭性）, 褶皱地壳构造, 海平面和气候变迁的影响, 地层厚度走向, 不整合 地图, 地震试验断面和横剖面 浅层地壳性质

表1 沉积非均质性尺度分类表[ 32] Table 1 Classification of scales of sedimentary heterogeneity[ 32]

目前在水文地质研究中就尺度转换问题的研究主要解决了两个问题：一是不同尺度下含水层的非均质性特征和随机性描述, 可以用蒙特卡洛方法和地质统计学（Kriging）方法定量描述含水层渗透系数的空间随机分布, 从而研究非均质含水层中的渗流与溶质迁移问题；二是运用随机数值模拟技术研究非均质含水层中的渗流与溶质迁移问题, 通过大尺度含水层渗流与溶质迁移数值模拟, 计算出大区域地下水变量的时空分布, 可以获得大尺度域内镶嵌的小尺度域的边界值；再计算小尺度域的渗流与溶质迁移问题, 之后再代入大尺度域内计算, 反复进行升尺度（upscaling）和降尺度(downscaling)数值分析, 从而解决尺度转换问题。

目前地下水尺度转换研究存在的问题：一是在应用过程中如何针对不同尺度分析非均质含水层中的渗流与溶质迁移, 尤其是污染物多相流迁移问题；二是从理论上还没有给出非均质含水层地下水计算的尺度转换关系式；三是如何应用有限的水文地质监测数据分析和描述不同尺度含水层的非均质特征, 不同尺度条件下需要多少监测数据才能分析含水层的非均质特征。

从地质的角度而言, 地下水渗流与溶质迁移模拟的不确定性主要来源于2个方面：地质结构构造和该构造条件下的水力参数值。而模型预测产生不确定主要来源有3类^{[ 59]}：①地质结构构造, ②有效模型参数, ③包含局部非均质性的模型参数。对于处理地质模型结构的不确定性, 最常用的处理方法是多模型平均法, 而多模型方法又分为手动多模型方法和统计多模型方法, 其中统计多模型方法较为常用, 也是目前研究地质结构构造不确定性最常用的方法。统计多模型是基于整个研究区满足平稳假设, 便可以通过随机模拟生成多个不确定性随机结构模型实现, 然后对这些随机模型求各个不同实现平均值用于渗流模拟计算。生成随机地质结构构造模型最常用的地统计模拟方法主要包括转换概率地质统计模拟（T-PROGS）^{[ 60]}和多点地质统计模拟（MPS）^{[ 61]}。近年来, 随着计算机的快速发展, 两者模型在模拟非均质含水层方面都得到了广泛的应用, 尤其是多点地质统计模拟。如Zhang等^{[ 62]}通过室内地层结构观测分析和地质统计模拟相结合的方法分析了一个典型试验沉积含水层的沉积结构特征。Lee等^{[ 63]}应用序贯高斯模拟（SGS）和转换概率地质统计模拟（T-PROGS）2种地质统计模拟方法通过条件模拟方法模拟劳伦斯Livermore国家实验室区的多个冲积含水层系统（LLNL）, 并对比了两者在模拟不同地质结构特征方面的优缺点。Hu and Chugunova^{[ 64]}综述了多点地质统计模拟在模拟非均质含水层结构方面的研究进展。在应用方面, Huysman等^{[ 65, 66]}采用野外露头调查和模拟相结合的方法, 应用多点地质统计模拟方法模拟了比利时真实含水层的结构特征, 并对污染羽状物在该含水层中的迁移演化特征进行了模拟分析。由于多点地质统计模拟是基于训练影像方法, 因此, 近年来, 在训练影像的取样方法以及训练影像技巧方面也有不少研究^{[ 67, 68]}。而有效模型参数的确定方法主要有蒙特卡洛分析（Monte Carlo analysis）和回归分析（Regression analysis）, 两者都是利用典型的线性化模型参数的协方差矩阵来定量化参数的不确定性以及推导预测的不确定性^{[ 59]}。而对于考虑包含局部非均质不确定性的模型参数, 常用的方法有高分辨率蒙特卡洛分析、回归分析以及矩方程方法。其中Neuman等^{[ 69]}指出矩方程的方法本质上可以认为是一种新的替代高分辨率蒙特卡洛分析方法。无论是非均质地质结构本身的不确定性预测还是模型参数的不确定性预测, 目前最常用的处理方法还是通过模型平均化方法, 即通过随机模拟生成多个实现, 从而求其平均值, 以达到减小模型预测误差的目的。

以上所述3种不确定性来源对模型预测的影响非常明显, 至于3种不确定性权重的来源往往各不相同, 主要取决于研究区的水文地质条件, 可用数据量以及模型预测的类型等。为描述地下水渗流与溶质迁移的不确定性, 人们通过随机的方法描述含水层介质的非均质性, 应用随机偏微分方程描述渗流和溶质迁移^{[ 70, 71]}。随之, 求解随机偏微分方程成为了解决不确定性问题的关键所在。蒙特卡洛方法（Monte Carlo method）是通过数值模拟求解随机偏微分方程最常用的方法, 在求解时仅需生成大量的非均质随机场（如渗透系数场）。蒙特卡洛方法是一种统计取样的方法, 因此, 其精度取决于生成随机场的实现数。而直接取样蒙特卡洛方法在概念上则比较简单且易于实现, 但是其缺点是计算量过大, 尤其对于大尺度问题^{[ 72]}。第2种方法是基于矩方程的方法^{[ 73, 74]}。该方法主要是通过推导一系列的确定性偏微分方程利用谱方法或一些闭合近似的手段来控制随机变量的统计矩（通常为前2阶矩）。对于大尺度问题而言, 该方法的缺点仍然是计算量太大。第3种方法是混沌多项式展开方法。该算法包括以混沌多项式为基础表示随机变量和使用伽辽金方法为展开系数推导近似离散方程。混沌多项式展开的优点是在特定条件下容许高阶近似随机变量以及拥有快速收敛的特性^{[ 72]}。Zhang 等^{[ 75]}提出一种基于Karhunen-Loeve展开（KLME）的矩方程计算方法, 并将该方法应用于随机非均质多孔介质渗流问题的计算, 研究表明该方法优于传统的一阶近似方法且计算效率高于蒙特卡洛方法。因此, 随后该方法在饱和-非饱和渗流问题求解^{[ 76]}以及溶质迁移问题^{[ 77]}等方面得到了应用。Li等^{[ 72]}结合了Karhunen-Loeve和混沌多项式展开提出了概率配点法（PCM）, 并将其与混沌多项式展开方法（PCE）以及Karhunen-Loeve展开方法（KLME）进行对比分析。

基于随机理论方法描述含水层参数的空间变异性时, 传统地质统计模拟方法往往假设含水层结构参数（如, 均值, 方差和协方差等）是已知的, 而对于实际含水层来说, 这些参数（如对数渗透系数方差和积分尺度等）都是未知的, Diggle等^{[ 78]}介绍了贝叶斯地质统计设计的概念。与地质统计或空间随机函数模拟法相比, 贝叶斯地统计设计容许地质统计模型本身存在不确定性。地质统计模型的不确定性可以包括均值的不确定性, 不确定性趋势系数, 协方差模型选择的不确定性以及协方差模型参数的不确定性。所有这些不确定性统称为结构不确定性。最近, Nowak等^{[ 79]}尝试应用贝叶斯地统计设计的方法处理参数不确定性问题。此外, 作为影响污染羽状物迁移行为的重要因素之一, 近年来, 非均质含水层中经常发生的横向混合作用也引起了不少学者的关注^{[ 33, 80]}。

从目前对于地下水污染物迁移数值模拟研究来看, 研究各有侧重点, 主要包括这三大方面：模型本身的建立与证明及其物理意义研究^{[ 6, 7, 81]}、模型求解计算研究^{[ 72, 75, 82]}以及模型在不同场地地质条件下应用研究^{[ 83, 84]}。到目前为止, 求解溶质迁移的数值模拟方法大致可以分为4类^{[ 85]}：欧拉法, 拉格朗日法, 混合欧拉—拉格朗日法和总变差下降法（TVD）。但是, 没有哪种数值方法适用于所有迁移条件, 因为这4种方法中都有各自的优点和局限性。基于拉格朗日法的随机游走粒子跟踪法（RWPT）的主要优点是计算效率高和不存在数值弥散问题, 而主要的问题是计算浓度的随机波动, 井处理和大变形网格遇到数值困难。与其他方法相比, 在求解以对流为主的渗流和溶质运移问题时, 选择随机游走粒子跟踪法较为适合, 因为可以有效的避免数值弥散和数值震荡。而混合欧拉-拉格朗日法则结合了欧拉法和拉格朗日法的优点, 即对流项用拉格朗日法处理, 弥散项用欧拉法处理, 但是, 大多数混合欧拉—拉格朗日法未能保证质量守恒并且其计算效率没有RWPT法高。而TVD法实际则是高阶有限差分方法, 本质上属于欧拉法求解技术范畴^{[ 86]}, 此类方法虽然能保证质量守恒以及减少数值弥散和数值震荡问题, 但是计算量远远大于拉格朗日法^{[ 85]}。总之, 对于求解弥散为主或求解含水层拥有较少的单元格和复杂的化学反应过程时, 选择标准对流—弥散模型（欧拉法）比较适合模拟污染物迁移, 而对于求解以对流为主的迁移问题时, 选择高空间分辨率或者多模型模拟方法, 如蒙特卡洛模拟或更高效的RWPT法则更合适。最近, Boso等^{[ 87]}对5种数值计算方法在计算模拟反应溶质和非反应溶质在非均质程度范围较大（非均质性方差σ²_Y=0.2~10之间）含水层中的计算精度进行了对比, 结果发现, 总变差下降法（TVD）和欧拉—拉格朗日特征线法（MOC）可广泛应用于各种计算模块, 而其他3种算法：随机游走粒子跟踪法（RWPT）, 平滑粒子流动动力学法（SPH）和基于流线的方法（SB-FV）则需要修正来提高精度。

基于欧拉法开发的计算程序（软件）主要有MODFLOW^{[ 88]}, MT3DMS^{[ 86]}和 FEFLOW^{[ 89]}。加拿大滑铁卢大学和拉瓦尔大学联合开发HydroGeoSphere^{[ 90]}（早期版本名为FRAC3DVS）, 该软件是用Fortran编写以及采用控制体积有限元法进行求解。由于其离散的灵活性以及适合处理复杂边界问题, 近年来该软件在模拟裂隙中的渗流和溶质运移^{[ 91]}和随机非均质含水层溶质运移模拟^{[ 58]}以及耦合孔隙—裂隙模拟^{[ 92]}等方面得到了较为广泛的应用。ParFlow是由美国劳伦斯利弗莫尔国家实验室（LLNL）开发的基于拉格朗日法（即粒子跟踪法）的数值模拟程序^{[ 93, 94]}, 该程序是开放的以及面向对象的并行流域水流模型软件。其包括完全集成地表渗流, 可以模拟复杂地形, 地质和非均质以及耦合陆面过程, 耦合包括土地-能源预算, 生物地球化学和降雪。Interactive Groundwater（IGW）^{[ 95]}则是由美国密西根州立大学Shu-Guang Li（李曙光）研究小组开发的基于有限元分析法的地下水流及污染物迁移模拟软件。IGW具有以下6个方面的特点^{[ 96]}：①实时概念建模；②实时渗流和迁移模拟；③实时分层建模；④实时随机模拟；⑤实时GIS制图；⑥实时模型分析。由于IGW软件特有的可实现区域大尺度和局部小尺度灵活转换及计算, 自开发以来被成功应用于模拟复杂多层区域地下水含水层中的渗流和溶质迁移问题^{[ 97, 98]}。

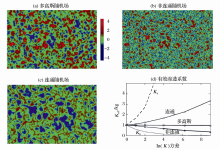
随着计算机技术的快速发展以及人们对含水层非均质性沉积以及其沉积结构研究的不断深入, 除了上述所提到的对非均质随机理论模型以及不确定性进行大量研究外, 近年来, 复杂沉积结构含水层的渗透连通性成为该领域一个新的研究热点。正如等Renard^{[ 99]}将最近50年来对含水层非均质性概化及模拟分为：综合等效平均化参数阶段、利用地质统计描述含水层小尺度非均质性（控制参数主要是对数渗透系数方差和相关长度）、同时考虑小尺度非均质性和沉积结构的连通性3个阶段。定量化描述含水层连通性是最近十几年的事。起初人们对地质介质非均质性对地下水渗流和溶质迁移的影响主要考虑了描述含水层本身非均质性结构特征（见图1a）, 也就是侧重于如何通过地质统计理论利用数值模拟手段再现含水层非均质性参数的空间分布。而随着研究的深入, 人们发现非均质含水层中高渗透性或低渗透性区的连通性对溶质迁移的影响非常明显, 通常连通性高渗透性区域往往形成优势流通道（preference flow channel）而低渗透性连通性区域则往往形成低渗透性墙（low-conductivity flow barriers）, 分别如图1b, 1c所示。而3种类型含水层的有效渗透系数大小关系则如图1d所示, 从图中可以看出, 未考虑连通性的多高斯随机场的有效渗透系数介于连通性和非连通性随机场之间。随后, Knudby等^{[ 100]}则首次给出了几种定量化描述渗流和溶质迁移连通性的计算方法, 通过指示地统计模拟发现迁移连通性与渗流连通性受含水层连通性结构影响存在较大差异, 并指出连通性是一个具有过程依赖性的概念。最近, 一些研究者通过数值模拟方法将非均质含水层连通性研究拓展到了三维的情况^{[ 101, 102]}, 从而揭示真实含水层空间结构连通性对渗流和溶质迁移的影响。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 不同类型渗流场及其相关渗流特性 Keff为有效渗透系数, Ka为渗透系数算术平均值, Kh为渗透系数调和平均值（据文献[103]修改）Fig. 1 Illustration of various types of fields and some results concerning their flow properties Keff is the effective conductivity, Ka the arithmetic mean and Kh the harmonic one (modified from reference[103])